HOC247 mß╗Øi c├Īc em c├╣ng xem T├│m tß║»t b├Āi giß║Żng B├Āi Hai mß║Ęt phß║│ng song song chŲ░ŲĪng tr├¼nh To├Īn lß╗øp 11 Kß║┐t Nß╗æi Tri Thß╗®c ph├Ła dŲ░ß╗øi ─æ├óy. Tß╗½ b├Āi n├Āy, c├Īc em sß║Į c├│ th├¬m mß╗Öt phŲ░ŲĪng ph├Īp ─æß╗ā chß╗®ng minh hai ─æŲ░ß╗Øng thß║│ng song song trong kh├┤ng gian. Ch├║c c├Īc em hß╗Źc tß║Łp vui vß║╗ v├Ā tr├Ān ─æß║¦y n─āng lŲ░ß╗Żng.
T├│m tß║»t l├Į thuyß║┐t
1.1. Hai mß║Ęt phß║│ng song song
|
Hai mß║Ęt phß║│ng (\(\alpha\)) v├Ā (\(\beta\)) ─æŲ░ß╗Żc gß╗Źi l├Ā song song vß╗øi nhau nß║┐u ch├║ng kh├┤ng c├│ ─æiß╗ām chung, k├Ł hiß╗ću (\(\alpha\)) // (\(\beta\)) hay (\(\beta\)) // (\(\alpha\)). |
Tß╗®c l├Ā: \((\alpha)//(\beta) \Leftrightarrow (\alpha) \cap (\beta) = \emptyset \)
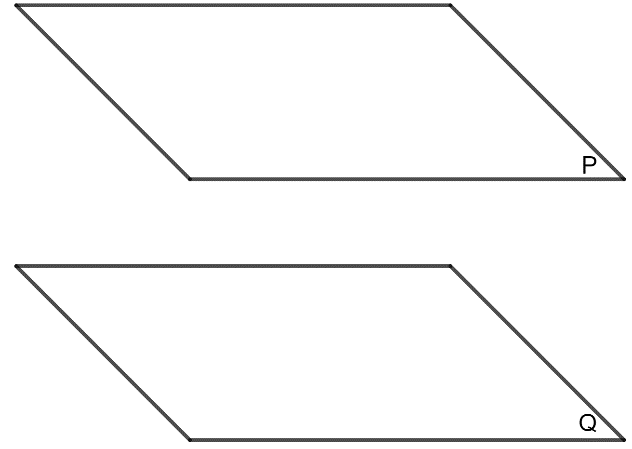
Nhß║Łn x├®t: Nß║┐u hai mß║Ęt phß║│ng (\(\alpha\)) // (\(\beta\)) v├Ā ─æŲ░ß╗Øng thß║│ng d \(\subset\) (\(\alpha\)) th├¼ d // (\(\beta\)).
1.2. ─Éiß╗üu kiß╗ćn v├Ā t├Łnh chß║źt cß╗¦a hai mß║Ęt phß║│ng song song
|
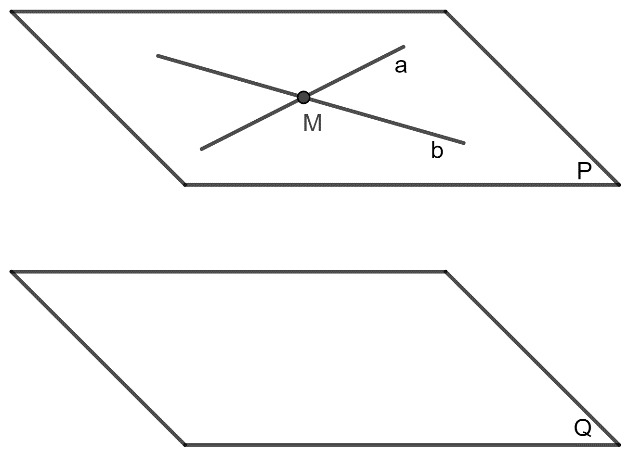
- Nß║┐u mß║Ęt phß║│ng (\(\alpha\)) chß╗®a hai ─æŲ░ß╗Øng thß║│ng cß║»t nhau v├Ā hai ─æŲ░ß╗Øng thß║│ng n├Āy song song vß╗øi mß║Ęt phß║│ng (\(\beta\)) th├¼ (\(\alpha\)) // (\(\beta\)). |
Tß╗®c l├Ā: \(\left\{ {\begin{array}{*{20}{l}} {a \subset \left( \alpha \right),b \subset \left( \alpha \right)}\\ {a \cap b = M}\\ {a//\left( \beta \right),b//\left( \beta \right)} \end{array}} \right. \Rightarrow \left( \alpha \right)//\left( \beta \right)\)
|
- Qua mß╗Öt ─æiß╗ām nß║▒m ngo├Āi mß╗Öt mß║Ęt phß║│ng cho trŲ░ß╗øc c├│ mß╗Öt v├Ā chß╗ē mß╗Öt mß║Ęt phß║│ng song song vß╗øi mß║Ęt phß║│ng ─æ├Ż cho. |
|
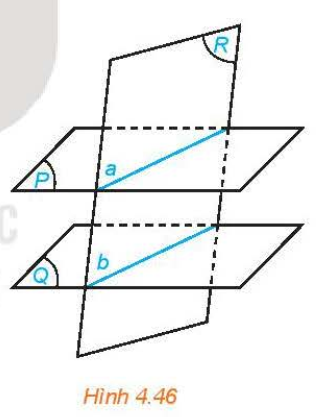
- Cho hai mß║Ęt phß║│ng song song. Nß║┐u mß╗Öt mß║Ęt phß║│ng cß║»t mß║Ęt phß║│ng n├Āy th├¼ c┼®ng cß║»t mß║Ęt phß║│ng kia v├Ā hai giao tuyß║┐n song song vß╗øi nhau. |
1.3. ─Éß╗ŗnh l├Į Thal├©s trong kh├┤ng gian
|
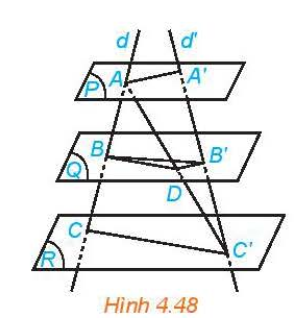
Ba mß║Ęt phß║│ng ─æ├┤i mß╗Öt song song chß║»n tr├¬n hai c├Īt tuyß║┐n ph├ón biß╗ćt bß║źt k├¼ nhß╗»ng ─æoß║Īn thß║│ng tŲ░ŲĪng ß╗®ng tß╗ē lß╗ć. |
Tß╗®c l├Ā: Nß║┐u ba mß║Ęt phß║│ng ─æ├┤i mß╗Öt song song (P), (Q), (R) cß║»t hai ─æŲ░ß╗Øng thß║│ng d v├Ā dŌĆÖ lß║¦n lŲ░ß╗Żt tß║Īi A, B, C v├Ā AŌĆÖ, BŌĆÖ, CŌĆÖ th├¼:
\(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{CA}}{{C'A'}}\)
1.4. H├¼nh l─āng trß╗ź v├Ā h├¼nh hß╗Öp
a) H├¼nh l─āng trß╗ź
|
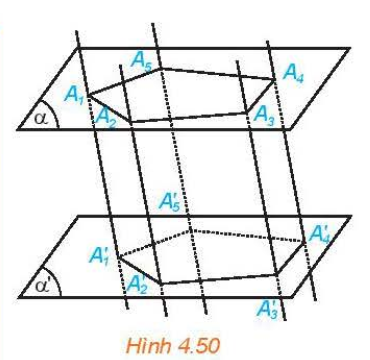
H├¼nh l─āng trß╗ź l├Ā mß╗Öt h├¼nh ─æa diß╗ćn c├│ hai mß║Ęt l├Ā hai ─æa gi├Īc nß║▒m trong hai mß║Ęt phß║│ng song song gß╗Źi l├Ā hai ─æ├Īy v├Ā tß║źt cß║Ż c├Īc cß║Īnh kh├┤ng thuß╗Öc hai mß║Ęt ─æ├Īy ─æß╗üu song song vß╗øi nhau. |
|
+ C├Īc ─æiß╗ām \({A_1},{A_2},...,{A_n}\) v├Ā \({A_1'},{A_2'},...,{A_n'}\) ─æŲ░ß╗Żc gß╗Źi l├Ā c├Īc ─æß╗ēnh. C├Īc ─æoß║Īn thß║│ng \({A_1}{A_1'},{A_2}{A_2'},...,{A_n}{A_n'}\) ─æŲ░ß╗Żc gß╗Źi l├Ā c├Īc cß║Īnh b├¬n. C├Īc ─æoß║Īn thß║│ng \({A_1}{A_2},{A_2}{A_3},...,{A_n}{A_1}\) v├Ā \({A_1'}{A_2'},{A_2'}{A_3'},...,{A_n'}{A_1'}\) ─æŲ░ß╗Żc gß╗Źi l├Ā cß║Īnh ─æ├Īy cß╗¦a h├¼nh l─āng trß╗ź. |
|
+ Hai ─æa gi├Īc \({A_1}{A_2}...{A_n}\) v├Ā \({A_1'}{A_2'}...{A_n'}\) ─æŲ░ß╗Żc gß╗Źi l├Ā hai mß║Ęt ─æ├Īy cß╗¦a h├¼nh l─āng trß╗ź. |
|
+ C├Īc tß╗® gi├Īc \({A_1}{A_1'}{A_2'}{A_2}, {A_2}{A_2'}{A_3'}{A_3},...,{A_n}{A_n'}{A_1'}{A_1}\) gß╗Źi l├Ā c├Īc mß║Ęt b├¬n cß╗¦a h├¼nh l─āng trß╗ź. |
Nhß║Łn x├®t: C├Īc mß║Ęt b├¬n cß╗¦a h├¼nh l─āng trß╗ź l├Ā h├¼nh b├¼nh h├Ānh. C├Īc cß║Īnh b├¬n ─æ├┤i mß╗Öt song song v├Ā c├│ ─æß╗Ö d├Āi bß║▒ng nhau.
Ch├║ ├Į: T├¬n cß╗¦a h├¼nh l─āng trß╗ź ─æŲ░ß╗Żc gß╗Źi dß╗▒a theo t├¬n cß╗¦a ─æa gi├Īc ─æ├Īy.
V├Ł dß╗ź:
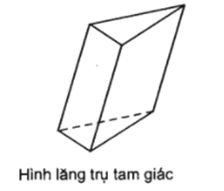
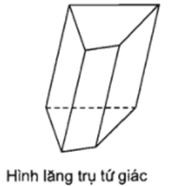
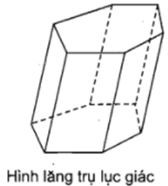
b) Hình hộp
|
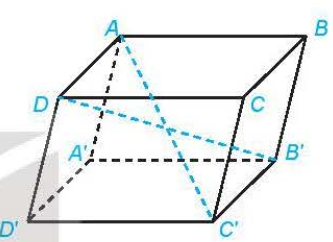
- H├¼nh hß╗Öp l├Ā h├¼nh l─āng trß╗ź tß╗® gi├Īc ABCD.A'B'C'D' c├│ hai ─æ├Īy l├Ā h├¼nh b├¼nh h├Ānh. |
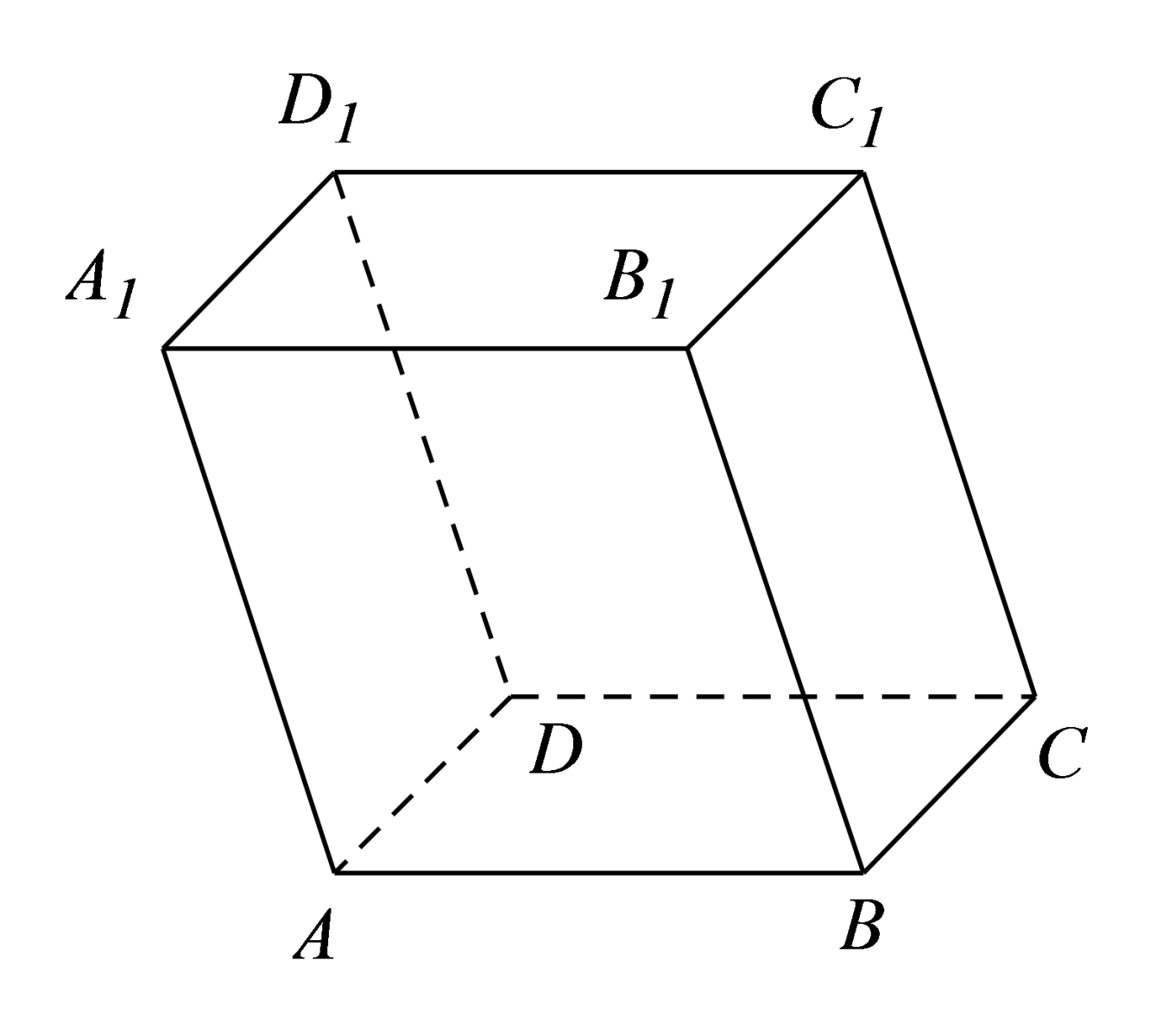
|
+ C├Īc cß║Ęp ─æiß╗ām A v├Ā C', B v├Ā D', C v├Ā A', D v├Ā B' ─æŲ░ß╗Żc gß╗Źi l├Ā c├Īc ─æß╗ēnh ─æß╗æi diß╗ćn cß╗¦a h├¼nh hß╗Öp. + C├Īc ─æoß║Īn thß║│ng AC', BD', CA' v├Ā DE' ─æŲ░ß╗Żc gß╗Źi l├Ā c├Īc ─æŲ░ß╗Øng ch├®o cß╗¦a h├¼nh hß╗Öp. |
| + C├Īc cß║Ęp tß╗® gi├Īc ABCD v├Ā A'B'C'D, ADD'A' v├Ā BCC'B', ABB'A' v├Ā CDDC ─æŲ░ß╗Żc gß╗Źi l├Ā hai mß║Ęt ─æß╗æi diß╗ćn cß╗¦a h├¼nh hß╗Öp. |
B├Āi tß║Łp minh hß╗Źa
B├Āi to├Īn 1: CHß╗©NG MINH HAI Mß║ČT PHß║▓NG SONG SONG
- PhŲ░ŲĪng ph├Īp: ─Éß╗ā chß╗®ng minh hai mß║Ęt phß║│ng song song ta c├│ thß╗ā thß╗▒c hiß╗ćn theo hŲ░ß╗øng sau:
+ Chß╗®ng minh trong mß║Ęt phß║│ng n├Āy c├│ hai ─æŲ░ß╗Øng thß║│ng cß║»t nhau c├╣ng song song vß╗øi mß║Ęt phß║│ng kia.
\(\left\{ \begin{array}{l}a \subset \left( \alpha \right),b \subset \left( \alpha \right)\\a \cap b = I\\a\parallel \left( \beta \right)\\b\parallel \left( \beta \right)\end{array} \right. \Rightarrow \left( \alpha \right)\parallel \left( \beta \right)\).
.png)
V├Ł dß╗ź 1:
Cho h├¼nh ch├│p \(S.ABCD\) c├│ ─æ├Īy \(ABCD\) l├Ā h├¼nh b├¼nh h├Ānh t├óm \(O\), gß╗Źi \(M,N\) lß║¦n lŲ░ß╗Żt l├Ā trung ─æiß╗ām cß╗¦a \(SA,SD\). Chß╗®ng minh \(\left( {OMN} \right)//\left( {SBC} \right)\).
HŲ░ß╗øng dß║½n giß║Żi:
.png)
Ta c├│ \(M,O\) lß║¦n lŲ░ß╗Żt l├Ā trung ─æiß╗ām cß╗¦a \(SA,AC\) n├¬n \(OM\) l├Ā ─æŲ░ß╗Øng trung b├¼nh cß╗¦a tam gi├Īc \(SAC\) ß╗®ng vß╗øi cß║Īnh \(SC\)do ─æ├│ \(OM\parallel SC\).
Vß║Ły \(\left\{ \begin{array}{l}OM\parallel SC\\SC \subset \left( {SBC} \right)\end{array} \right. \Rightarrow OM\parallel \left( {SBC} \right){\rm{ }}\left( 1 \right)\).
TŲ░ŲĪng tß╗▒, Ta c├│ \(N,O\) lß║¦n lŲ░ß╗Żt l├Ā trung ─æiß╗ām cß╗¦a \(SD,BD\) n├¬n \(ON\) l├Ā ─æŲ░ß╗Øng trung b├¼nh cß╗¦a tam gi├Īc \(SBD\) ß╗®ng vß╗øi cß║Īnh \(SB\)do ─æ├│ \(OM//SB\).
Vß║Ły \(\left\{ \begin{array}{l}ON\parallel SB\\SB \subset \left( {SBC} \right)\end{array} \right. \Rightarrow OM\parallel \left( {SBC} \right){\rm{ }}\left( 2 \right)\). Tß╗½ \(\left( 1 \right)\) v├Ā \(\left( 2 \right)\) ta c├│ \(\left\{ \begin{array}{l}OM\parallel \left( {SBC} \right)\\ON\parallel \left( {SBC} \right)\\OM \cap ON = O\end{array} \right. \Rightarrow \left( {OMN} \right)\parallel \left( {SBC} \right)\).
B├Āi to├Īn 2: X├üC ─Éß╗ŖNH THIß║ŠT DIß╗åN Cß╗”A \(\left( \alpha \right)\) Vß╗ÜI H├īNH CH├ōP KHI BIß║ŠT \(\left( \alpha \right)\) SONG SONG Vß╗ÜI Mß╗śT Mß║ČT PHß║▓NG \(\left( \beta \right)\) CHO TRŲ»ß╗ÜC
- PhŲ░ŲĪng ph├Īp: ─Éß╗ā x├Īc ─æß╗ŗnh thiß║┐t diß╗ćn trong trŲ░ß╗Øng hß╗Żp n├Āy ta sß╗Ł dß╗źng c├Īc t├Łnh chß║źt sau.
+ Khi \(\left( \alpha \right)\parallel \left( \beta \right)\) th├¼ \(\left( \alpha \right)\) song song vß╗øi tß║źt cß║Ż c├Īc ─æŲ░ß╗Øng thß║│ng trong \(\left( \beta \right)\) v├Ā ta chuyß╗ān vß╗ü dß║Īng thiß║┐t diß╗ćn song song vß╗øi ─æŲ░ß╗Øng thß║│ng.
+ Sß╗Ł dß╗źng \(\left\{ \begin{array}{l}\left( \alpha \right)\parallel \left( \beta \right)\\\left( \beta \right)\parallel \left( \gamma \right)\\\left( \beta \right) \cap \left( \gamma \right) = d\\M \in \left( \alpha \right) \cap \left( \gamma \right)\end{array} \right. \Rightarrow \left( \alpha \right) \cap \left( \gamma \right) = d'\parallel d,M \in d'\).
+ T├¼m ─æŲ░ß╗Øng thß║│ng \(d\) mß║▒n trong \(\left( \beta \right)\) v├Ā x├®t c├Īc mß║Ęt phß║│ng c├│ trong h├¼nh ch├│p m├Ā chß╗®a \(d\), khi ─æ├│ \(\left( \alpha \right)\parallel d\) n├¬n sß║Į cß║»t c├Īc mß║Ęt phß║│ng chß╗®a \(d\) (nß║┐u c├│) theo c├Īc giao tuyß║┐n song song vß╗øi \(d\).
V├Ł dß╗ź 2:
Cho h├¼nh ch├│p \(S.ABCD\) c├│ ─æ├Īy \(ABCD\) l├Ā h├¼nh b├¼nh h├Ānh v├Ā \(M,N\) lß║¦n lŲ░ß╗Żt l├Ā trung ─æiß╗ām cß╗¦a \(AB,CD\). X├Īc ─æß╗ŗnh thiß║┐t diß╗ćn cß╗¦a h├¼nh ch├│p cß║»t bß╗¤i \(\left( \alpha \right)\) ─æi qua \(MN\) v├Ā song song vß╗øi mß║Ęt phß║│ng \(\left( {SAD} \right)\). Thiß║┐t diß╗ćn l├Ā h├¼nh g├¼?
HŲ░ß╗øng dß║½n giß║Żi:
.png)
Ta c├│ \(\left\{ \begin{array}{l}M \in \left( {SAB} \right) \cap \left( \alpha \right)\\\left( {SAB} \right) \cap \left( {SAD} \right) = SA\end{array} \right.\)\( \Rightarrow \left( {SAB} \right) \cap \left( \alpha \right) = MK\parallel SA,K \in SB\).
TŲ░ŲĪng tß╗▒ \(\left\{ \begin{array}{l}N \in \left( {SCD} \right) \cap \left( \alpha \right)\\\left( \alpha \right)\parallel \left( {SAD} \right)\\\left( {SCD} \right) \cap \left( {SAD} \right) = SD\end{array} \right.\) \( \Rightarrow \left( {SCD} \right) \cap \left( \alpha \right) = NH\parallel SD,H \in SC\).
Dß╗ģ thß║źy \(HK = \left( \alpha \right) \cap \left( {SBC} \right)\). Thiß║┐t diß╗ćn l├Ā tß╗® gi├Īc \(MNHK\)
Ba mß║Ęt phß║│ng \(\left( {ABCD} \right),\left( {SBC} \right)\) v├Ā \(\left( \alpha \right)\) ─æ├┤i mß╗Öt cß║»t nhau theo c├Īc giao tuyß║┐n l├Ā \(MN,HK,BC\), m├Ā \(MN\parallel BC \Rightarrow MN\parallel HK\).
Vß║Ły thiß║┐t diß╗ćn l├Ā mß╗Öt h├¼nh thang.
Luyß╗ćn tß║Łp B├Āi 13 To├Īn 11 Kß║┐t Nß╗æi Tri Thß╗®c
Hß╗Źc xong b├Āi hß╗Źc n├Āy, em c├│ thß╗ā:
- Nhß║Łn biß║┐t hai mß║Ęt phß║│ng song song trong kh├┤ng gian. Giß║Żi th├Łch ─æiß╗üu kiß╗ćn ─æß╗ā hai mß║Ęt phß║│ng song song. Giß║Żi th├Łch t├Łnh chß║źt cŲĪ bß║Żn vß╗ü hai mß║Ęt phß║│ng song song.
- Giß║Żi th├Łch ─æß╗ŗnh l├Ł Thales trong kh├┤ng gian. Giß║Żi th├Łch t├Łnh chß║źt cŲĪ bß║Żn cß╗¦a h├¼nh l─āng trß╗ź v├Ā h├¼nh hß╗Öp. M├┤ tß║Ż mß╗Öt sß╗æ h├¼nh ß║Żnh trong thß╗▒c tiß╗ģn c├│ li├¬n quan ─æß║┐n hai mß║Ęt phß║│ng song song trong kh├┤ng gian.
3.1. Trß║»c nghiß╗ćm B├Āi 13 To├Īn 11 Kß║┐t Nß╗æi Tri Thß╗®c
C├Īc em c├│ thß╗ā hß╗ć thß╗æng lß║Īi nß╗Öi dung kiß║┐n thß╗®c ─æ├Ż hß╗Źc ─æŲ░ß╗Żc th├┤ng qua b├Āi kiß╗ām tra Trß║»c nghiß╗ćm To├Īn 11 Kß║┐t nß╗æi tri thß╗®c ChŲ░ŲĪng 4 B├Āi 13 cß╗▒c hay c├│ ─æ├Īp ├Īn v├Ā lß╗Øi giß║Żi chi tiß║┐t.
-
- A. a v├Ā b song song.
- B. a v├Ā b ch├®o nhau.
- C. a v├Ā b tr├╣ng nhau.
- D. a v├Ā b cß║»t nhau.
-
Câu 2:
Chß╗Źn C├óu ─æ├║ng :
- A. Hai ─æŲ░ß╗Øng thß║│ng a v├Ā b kh├┤ng c├╣ng nß║▒m trong mß║Ęt phß║│ng (P) n├¬n ch├║ng ch├®o nhau.
- B. Hai ─æŲ░ß╗Øng thß║│ng kh├┤ng song song th├¼ ch├®o nhau.
- C. Hai ─æŲ░ß╗Øng thß║│ng ph├ón biß╗ćt lß║¦n lŲ░ß╗Żt nß║▒m tr├¬n hai mß║Ęt phß║│ng kh├Īc nhau th├¼ ch├®o nhau.
- D. Hai ─æŲ░ß╗Øng thß║│ng kh├┤ng song song v├Ā lß║¦n lŲ░ß╗Żt nß║▒m tr├¬n hai mß║Ęt phß║│ng song song th├¼ ch├®o nhau.
-
Câu 3:
Chß╗Źn C├óu ─æ├║ng :
- A. Hai mß║Ęt phß║│ng ph├ón biß╗ćt c├╣ng song song vß╗øi mß║Ęt phß║│ng thß╗® ba th├¼ ch├║ng song song.
- B. Hai ─æŲ░ß╗Øng thß║│ng c├╣ng song song vß╗øi mß╗Öt mß║Ęt phß║│ng th├¼ song song vß╗øi nhau.
- C. Hai mß║Ęt phß║│ng kh├┤ng cß║»t nhau th├¼ song song.
- D. Hai mß║Ęt phß║│ng kh├┤ng song song th├¼ tr├╣ng nhau.
C├óu 4-10: Mß╗Øi c├Īc em ─æ─āng nhß║Łp xem tiß║┐p nß╗Öi dung v├Ā thi thß╗Ł Online ─æß╗ā cß╗¦ng cß╗æ kiß║┐n thß╗®c vß╗ü b├Āi hß╗Źc n├Āy nh├®!
3.2. B├Āi tß║Łp SGK B├Āi 13 To├Īn 11 Kß║┐t Nß╗æi Tri Thß╗®c
C├Īc em c├│ thß╗ā xem th├¬m phß║¦n hŲ░ß╗øng dß║½n Giß║Żi b├Āi tß║Łp To├Īn 11 Kß║┐t nß╗æi tri thß╗®c ChŲ░ŲĪng 4 B├Āi 13 ─æß╗ā gi├║p c├Īc em nß║»m vß╗»ng b├Āi hß╗Źc v├Ā c├Īc phŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp.
Mß╗¤ ─æß║¦u trang 88 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Hoß║Īt ─æß╗Öng 1 trang 88 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Giß║Żi C├óu hß╗Åi trang 88 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Hoß║Īt ─æß╗Öng 2 trang 89 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Giß║Żi C├óu hß╗Åi trang 89 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Luyß╗ćn tß║Łp 1 trang 89 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Vß║Łn dß╗źng 1 trang 89 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Hoß║Īt ─æß╗Öng 3 trang 89 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Giß║Żi C├óu hß╗Åi trang 89 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Luyß╗ćn tß║Łp 2 trang 90 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Hoß║Īt ─æß╗Öng 4 trang 90 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Luyß╗ćn tß║Łp 3 trang 91 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Hoß║Īt ─æß╗Öng 5 trang 91 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Luyß╗ćn tß║Łp 4 trang 91 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Hoß║Īt ─æß╗Öng 6 trang 91 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Giß║Żi C├óu hß╗Åi trang 92 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Luyß╗ćn tß║Łp 5 trang 92 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Hoß║Īt ─æß╗Öng 7 trang 92 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Luyß╗ćn tß║Łp 6 trang 93 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Vß║Łn dß╗źng 2 trang 93 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Giß║Żi B├Āi 4.21 trang 93 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Giß║Żi B├Āi 4.22 trang 94 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Giß║Żi B├Āi 4.23 trang 94 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Giß║Żi B├Āi 4.24 trang 94 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Giß║Żi B├Āi 4.25 trang 94 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Giß║Żi B├Āi 4.26 trang 94 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Giß║Żi B├Āi 4.27 trang 94 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Giß║Żi B├Āi 4.28 trang 94 SGK To├Īn 11 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Ba╠Ći t├ó╠Żp 4.29 trang 67 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Ba╠Ći t├ó╠Żp 4.30 trang 67 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Ba╠Ći t├ó╠Żp 4.31 trang 67 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Ba╠Ći t├ó╠Żp 4.32 trang 67 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Ba╠Ći t├ó╠Żp 4.33 trang 68 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Ba╠Ći t├ó╠Żp 4.34 trang 68 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Ba╠Ći t├ó╠Żp 4.35 trang 68 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Ba╠Ći t├ó╠Żp 4.36 trang 68 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Ba╠Ći t├ó╠Żp 4.37 trang 68 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Ba╠Ći t├ó╠Żp 4.38 trang 68 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Ba╠Ći t├ó╠Żp 4.39 trang 68 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Ba╠Ći t├ó╠Żp 4.40 trang 68 SBT Toa╠ün 11 T├ó╠Żp 1 K├¬╠üt n├┤╠üi tri thŲ░╠üc - KNTT
Hß╗Åi ─æ├Īp B├Āi 13 To├Īn 11 Kß║┐t Nß╗æi Tri Thß╗®c
Trong qu├Ī tr├¼nh hß╗Źc tß║Łp nß║┐u c├│ thß║»c mß║»c hay cß║¦n trß╗Ż gi├║p g├¼ th├¼ c├Īc em h├Ży comment ß╗¤ mß╗źc Hß╗Åi ─æ├Īp, Cß╗Öng ─æß╗ōng To├Īn hß╗Źc HOC247 sß║Į hß╗Ś trß╗Ż cho c├Īc em mß╗Öt c├Īch nhanh ch├│ng!
Ch├║c c├Īc em hß╗Źc tß║Łp tß╗æt v├Ā lu├┤n ─æß║Īt th├Ānh t├Łch cao trong hß╗Źc tß║Łp!
-- Mod To├Īn Hß╗Źc 11 Hß╗īC247





.PNG)






