HŲ░ß╗øng dß║½n Giß║Żi b├Āi tß║Łp To├Īn 10 Kß║┐t nß╗æi tri thß╗®c B├Āi tß║Łp cuß╗æi chŲ░ŲĪng 3 B├Āi tß║Łp cuß╗æi chŲ░ŲĪng 3 gi├║p c├Īc em hß╗Źc sinh nß║»m vß╗»ng phŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp v├Ā ├┤n luyß╗ćn tß╗æt kiß║┐n thß╗®c.
-
Giß║Żi b├Āi 3.12 trang 44 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Cho tam gi├Īc ABC c├│ \(\widehat B = {135^o}\). Khß║│ng ─æß╗ŗnh n├Āo sau ─æ├óy l├Ā ─æ├║ng?
a)
A. \(S = \frac{1}{2}ca\)
B. \(S = \frac{{ - \sqrt 2 }}{4}ac\)
C. \(S = \frac{{\sqrt 2 }}{4}bc\)
D. \(S = \frac{{\sqrt 2 }}{4}ca\)
b)
A. \(R = \frac{a}{{\sin A}}\)
B. \(R = \frac{{\sqrt 2 }}{2}b\)
C. \(R = \frac{{\sqrt 2 }}{2}c\)
D. \(R = \frac{{\sqrt 2 }}{2}a\)
c)
A. \({a^2} = {b^2} + {c^2} + \sqrt 2 ab.\)
B. \(\frac{b}{{\sin A}} = \frac{a}{{\sin B}}\)
C. \(\sin B = \frac{{ - \sqrt 2 }}{2}\)
D. \({b^2} = {c^2} + {a^2} - 2ca\cos {135^o}.\)
-
Giß║Żi b├Āi 3.13 trang 44 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Cho tam gi├Īc ABC. Khß║│ng ─æß╗ŗnh n├Āo sau ─æ├óy l├Ā ─æ├║ng?
a)
A. \(S = \frac{{abc}}{{4r}}\)
B. \(r = \frac{{2S}}{{a + b + c}}\)
C. \({a^2} = {b^2} + {c^2} + 2bc\;\cos A\)
D. \(S = r\,(a + b + c)\)
b)
A. \(\sin A = \sin \,(B + C)\)
B. \(\cos A = \cos \,(B + C)\)
C. \(\;\cos A > 0\)
D. \(\sin A\,\, \le 0\)
-
Giß║Żi b├Āi 3.14 trang 44 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
T├Łnh gi├Ī trß╗ŗ cß╗¦a c├Īc biß╗āu thß╗®c sau:
a) \(M = \sin {45^o}.\cos {45^o} + \sin {30^o}\)
b) \(N = \sin {60^o}.\cos {30^o} + \frac{1}{2}.\sin {45^o}\)
c) \(P = 1 + {\tan ^2}{60^o}\)
d) \(Q = \frac{1}{{{{\sin }^2}{{120}^o}}} - {\cot ^2}{120^o}.\)
-
Giß║Żi b├Āi 3.15 trang 44 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Cho tam gi├Īc ABC c├│ \(\widehat B = {60^o},\;\,\widehat C = {45^o},AC = 10\). T├Łnh \(a,R,S,r\).
-
Giß║Żi b├Āi 3.16 trang 44 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Cho tam gi├Īc ABC c├│ trung tuyß║┐n AM. Chß╗®ng minh rß║▒ng:
a) \(\cos \widehat {AMB} + \cos \widehat {AMC} = 0\)
b) \(M{A^2} + M{B^2} - A{B^2} = 2.MA.MB.\cos \widehat {AMB}\) v├Ā \(M{A^2} + M{C^2} - A{C^2} = 2.MA.MC.\cos \widehat {AMC}\)
c) \(M{A^2} = \frac{{2\left( {A{B^2} + A{C^2}} \right) - B{C^2}}}{4}\) (c├┤ng thß╗®c ─æŲ░ß╗Øng trung tuyß║┐n).
-
Giß║Żi b├Āi 3.17 trang 44 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Cho tam gi├Īc ABC. Chß╗®ng minh rß║▒ng:
a) Nß║┐u g├│c A nhß╗Źn th├¼ \({b^2} + {c^2} > {a^2}\)
b) Nếu góc A tù thì \({b^2} + {c^2} < {a^2}\)
c) Nếu góc A vuông thì \({b^2} + {c^2} = {a^2}\)
-
Giß║Żi b├Āi 3.18 trang 45 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Tr├¬n biß╗ān, t├Āu B ß╗¤ vß╗ŗ tr├Ł c├Īch t├Āu A 53km vß╗ü hŲ░ß╗øng \(N{34^o}E\). Sau ─æ├│, t├Āu B chuyß╗ān ─æß╗Öng thß║│ng ─æß╗üu vß╗øi vß║Łn tß╗æc c├│ ─æß╗Ö lß╗øn 30 km/h vß╗ü hŲ░ß╗øng ─æ├┤ng v├Ā t├Āu A chuyß╗ān ─æß╗Öng thß║│ng ─æß╗üu vß╗øi vß║Łn tß╗æc c├│ ─æß╗Ö lß╗øn 50 km/h ─æß╗ā ─æuß╗Ģi kß╗ŗp t├Āu B.
a) Hß╗Åi t├Āu A cß║¦n phß║Żi chuyß╗ān ─æß╗Öng theo hŲ░ß╗øng n├Āo?
b) Vß╗øi hŲ░ß╗øng chuyß╗ān ─æß╗Öng ─æ├│ th├¼ sau bao l├óu t├Āu A ─æuß╗Ģi kß╗ŗp t├Āu B?
-
Giß║Żi b├Āi 3.19 trang 45 SGK To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Tr├¬n s├ón b├│ng ch├Āy d├Ānh cho nam, c├Īc vß╗ŗ tr├Ł g├┤n Nh├Ā (Home plate), g├┤n 1 (First base), g├┤n 2 (Second base), g├┤n 3 (Third base) l├Ā bß╗æn ─æß╗ēnh cß╗¦a mß╗Öt h├¼nh vu├┤ng c├│ cß║Īnh d├Āi 27,4 m. Vß╗ŗ tr├Ł ─æß╗®ng n├®m b├│ng (PitcherŌĆÖs mound) nß║▒m tr├¬n ─æŲ░ß╗Øng nß╗æi g├┤n Nh├Ā vß╗øi g├┤n 2, v├Ā c├Īch g├┤n Nh├Ā 18,44 m. T├Łnh c├Īc khoß║Żng c├Īch tß╗½ vß╗ŗ tr├Ł ─æß╗®ng n├®m b├│ng tß╗øi c├Īc g├┤n 1 v├Ā g├┤n 3.
-
Giß║Żi b├Āi 3.17 trang 40 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Tam gi├Īc \(ABC\) c├│ \(\widehat A = {15^ \circ },\,\,\widehat B = {45^ \circ }.\) Gi├Ī trß╗ŗ cß╗¦a \(\tan C\) bß║▒ng:
A. \( - \sqrt 3 .\)
B. \(\sqrt 3 .\)
C. \(\frac{1}{{\sqrt 3 }}.\)
D. \( - \frac{1}{{\sqrt 3 }}.\)
-
Giß║Żi b├Āi 3.18 trang 40 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Tr├¬n mß║Ęt phß║│ng tß╗Źa ─æß╗Ö \(Oxy,\) lß║źy ─æiß╗ām \(M\) thuß╗Öc nß╗Ła ─æŲ░ß╗Øng tr├▓n ─æŲĪn vß╗ŗ sao cho \(\widehat {xOM} = {135^ \circ }.\) T├Łch ho├Ānh ─æß╗Ö v├Ā tung ─æß╗Ö cß╗¦a ─æiß╗ām \(M\) bß║▒ng
A. \(\frac{1}{{2\sqrt 2 }}.\)
B. \(\frac{1}{2}\)
C. \( - \frac{1}{2}\)
D. \( - \frac{1}{{2\sqrt 2 }}.\)
-
Giß║Żi b├Āi 3.19 trang 40 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Tr├¬n mß║Ęt phß║│ng tß╗Źa ─æß╗Ö \(Oxy,\) lß║źy ─æiß╗ām \(M\) thuß╗Öc nß╗Ła ─æŲ░ß╗Øng tr├▓n ─æŲĪn vß╗ŗ sao cho \(\widehat {xOM} = {150^ \circ }.\) \(N\) l├Ā ─æiß╗ām ─æß╗æi xß╗®ng vß╗øi \(M\) qua trß╗źc tung. Gi├Ī trß╗ŗ cß╗¦a \(\tan \widehat {xON}\) bß║▒ng:
A. \(\frac{1}{{\sqrt 3 }}.\)
B. \( - \frac{1}{{\sqrt 3 }}.\)
C. \(\sqrt 3 .\)
D. \( - \sqrt 3 .\)
-
Giß║Żi b├Āi 3.20 trang 40 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Cho g├│c nhß╗Źn \(\alpha \) c├│ \(\tan \alpha = \frac{3}{4}.\) Gi├Ī trß╗ŗ cß╗¦a \(\sin \alpha .\cos \alpha \) bß║▒ng
A. \(\frac{4}{3}.\)
B. \(\frac{{12}}{{25}}.\)
C. \(\frac{{25}}{{12}}.\)
D. \(\frac{3}{4}.\)
-
Giß║Żi b├Āi 3.21 trang 40 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Cho g├│c nhß╗Źn \(\alpha \,\,\left( {{0^ \circ } < \alpha < {{180}^ \circ }} \right)\) thß╗Åa m├Żn \(\sin \alpha + \cos \alpha = 1.\) Gi├Ī trß╗ŗ cß╗¦a \(\cot \alpha \) bß║▒ng:
A. \(0.\)
B. \(1.\)
C. \( - 1.\)
D. Kh├┤ng tß╗ōn tß║Īi
-
Giß║Żi b├Āi 3.22 trang 40 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Cho g├│c \(\alpha \) thß╗Åa m├Żn \(\sin \alpha + \cos \alpha = \sqrt 2 .\) Gi├Ī trß╗ŗ cß╗¦a \(\tan \alpha + \cot \alpha \) l├Ā:
A. 1.
B. \( - 2\).
C. 0.
D. 2.
-
Giß║Żi b├Āi 3.23 trang 40 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Tr├¬n mß║Ęt phß║│ng tß╗Źa ─æß╗Ö \(Oxy,\) lß║źy ─æiß╗ām \(M\) thuß╗Öc nß╗Ła ─æŲ░ß╗Øng tr├▓n ─æŲĪn vß╗ŗ, sao cho \(\cos \widehat {xOM} = \frac{{ - 3}}{5}.\) (H.3.4). Diß╗ćn t├Łch cß╗¦a tam gi├Īc \(AOM\) bß║▒ng:
A. \(\frac{4}{5}.\)
B. \(\frac{2}{5}.\)
C. \(\frac{3}{5}.\)
D. \(\frac{3}{{10}}.\)
-
Giß║Żi b├Āi 3.24 trang 41 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
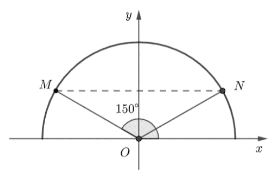
Tr├¬n mß║Ęt phß║│ng tß╗Źa ─æß╗Ö \(Oxy,\) lß║źy ─æiß╗ām \(M\) thuß╗Öc nß╗Ła ─æŲ░ß╗Øng tr├▓n ─æŲĪn vß╗ŗ sao cho \(\widehat {xOM} = {150^ \circ }\)(H.3.5). \(N\) l├Ā ─æiß╗ām ─æß╗æi xß╗®ng vß╗øi \(M\) qua trß╗źc tung. Diß╗ćn t├Łch cß╗¦a tam gi├Īc \(MAN\) bß║▒ng:
A. \(\frac{{\sqrt 3 }}{4}.\)
B. \(\frac{{\sqrt 3 }}{2}.\)
C. \(\sqrt 3 .\)
D. \(2\sqrt 3 .\)
-
Giß║Żi b├Āi 3.25 trang 41 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Cho \(\cos \alpha = \frac{1}{4}.\) Gi├Ī trß╗ŗ cß╗¦a \(P = \frac{{\tan \alpha + 2\cot \alpha }}{{2\tan \alpha + 3\cot \alpha }}\) l├Ā:
A. \( - \frac{{17}}{{33}}.\)
B. \(\frac{{17}}{{33}}.\)
C. \(\frac{1}{2}.\)
D. \(\frac{{16}}{{33}}.\)
-
Giß║Żi b├Āi 3.26 trang 41 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Tam gi├Īc \(ABC\) c├│ \(a = 2,\,\,b = 3,\,\,c = 4.\) B├Īn k├Łnh ─æŲ░ß╗Øng tr├▓n ngoß║Īi tiß║┐p cß╗¦a tam gi├Īc \(ABC\) l├Ā:
A. \(R = \frac{{\sqrt {15} }}{2}.\)
B. \(R = \frac{7}{{\sqrt {15} }}.\)
C. \(R = \frac{{\sqrt {15} }}{6}.\)
D. \(R = \frac{8}{{\sqrt {15} }}.\)
-
Giß║Żi b├Āi 3.27 trang 41 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Tam gi├Īc \(ABC\) c├│ \(a = 4,\,\,b = 5,\,\,c = 6.\) ─Éß╗Ö d├Āi ─æŲ░ß╗Øng cao \({h_b}\) bß║▒ng:
A. \(\frac{{3\sqrt 7 }}{2}.\)
B. \(\frac{3}{{2\sqrt 7 }}.\)
C. \(\frac{{3\sqrt 7 }}{4}.\)
D. \(\frac{3}{{4\sqrt 7 }}.\)
-
Giß║Żi b├Āi 3.28 trang 41 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Cho tam gi├Īc \(ABC\) c├│ \(a = 20,\,\,b = 16\) v├Ā \({m_a} = 10.\) Diß╗ćn t├Łch cß╗¦a tam gi├Īc bß║▒ng:
A. \(92.\)
B. \(100.\)
C. \(96.\)
D. \(88.\)
-
Giß║Żi b├Āi 3.29 trang 41 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Tam gi├Īc \(ABC\) c├│ \(a = 14,\,\,b = 9\) v├Ā \({m_a} = 8.\) ─Éß╗Ö d├Āi ─æŲ░ß╗Øng cao \({h_a}\) bß║▒ng:
A. \(\frac{{24\sqrt 5 }}{7}.\)
B. \(\frac{{12\sqrt 5 }}{7}.\)
C. \(12\sqrt 5 .\)
D. \(24\sqrt 5 .\)
-
Giß║Żi b├Āi 3.30 trang 42 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Tam gi├Īc \(ABC\) c├│ \(\widehat A = {45^ \circ },\,\,c = 6,\,\,\widehat B = {75^ \circ }.\)
─Éß╗Ö d├Āi ─æŲ░ß╗Øng cao \({h_b}\) bß║▒ng:
A. \(3\sqrt 2 .\)
B. \(\frac{3}{{\sqrt 2 }}.\)
C. \(6\sqrt 2 .\)
D. \(2\sqrt 3 .\)
-
Giß║Żi b├Āi 3.31 trang 42 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Tam gi├Īc \(ABC\) c├│ \(\widehat A = {45^ \circ },\,\,c = 6,\,\,\widehat B = {75^ \circ }.\) ─Éß╗Ö d├Āi b├Īn k├Łnh ─æŲ░ß╗Øng tr├▓n ngoß║Īi tiß║┐p cß╗¦a tam gi├Īc bß║▒ng:
A. \(8\sqrt 3 .\)
B. \(2\sqrt 3 .\)
C. \(6\sqrt 3 .\)
D. \(4\sqrt 3 .\)
-
Giß║Żi b├Āi 3.32 trang 42 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Tam gi├Īc \(ABC\) c├│ diß╗ćn t├Łch \(S = 2R{}^2.\sin B.\sin C,\) vß╗øi \(R\) l├Ā ─æß╗Ö d├Āi b├Īn k├Łnh ─æŲ░ß╗Øng tr├▓n ngoß║Īi tiß║┐p tam gi├Īc. Sß╗æ ─æo g├│c \(A\) bß║▒ng:
A. \({60^ \circ }\)
B. \({90^ \circ }\)
C. \({30^ \circ }\)
D. \({75^ \circ }\)
-
Giß║Żi b├Āi 3.33 trang 42 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Tam gi├Īc \(ABC\) c├│ \(AB = \sqrt 5 ,\,\,AC = \sqrt 2 ,\,\,\widehat C = {45^ \circ }.\) ─Éß╗Ö d├Āi cß║Īnh \(BC\) bß║▒ng:
A. \(3.\)
B. \(2.\)
C. \(\sqrt 3 .\)
D. \(\sqrt 2 .\)
-
Giß║Żi b├Āi 3.34 trang 42 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Tam gi├Īc \(ABC\) c├│ \(\widehat C = {60^ \circ },\,\,AC = 2,\,\,AB = \sqrt 7 .\) Diß╗ćn t├Łch cß╗¦a tam gi├Īc \(ABC\) bß║▒ng:
A. \(\frac{{\sqrt 3 }}{2}.\)
B. \(3\sqrt 3 .\)
C. \(\frac{{3\sqrt 3 }}{2}.\)
D. \(\sqrt 3 .\)
-
Giß║Żi b├Āi 3.35 trang 42 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Tam gi├Īc \(ABC\) c├│ \(\widehat A = {60^ \circ },\,\,AB = 3,\,\,BC = 3\sqrt 3 .\) ─Éß╗Ö d├Āi b├Īn k├Łnh ─æŲ░ß╗Øng tr├▓n nß╗Öi tiß║┐p cß╗¦a tam gi├Īc \(ABC\) l├Ā:
A. \(\frac{{3\left( {\sqrt 3 - 1} \right)}}{2}.\)
B. \(\frac{{3\left( {\sqrt 3 + 1} \right)}}{2}.\)
C. \(\frac{{\sqrt 3 - 1}}{2}.\)
D. \(\sqrt 3 - 1.\)
-
Giß║Żi b├Āi 3.36 trang 43 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Mß╗Öt ca n├┤ xuß║źt ph├Īt tß╗½ cß║Żng A, chß║Īy theo hŲ░ß╗øng ─æ├┤ng vß╗øi tß╗æc ─æß╗Ö 60 km/h. C├╣ng l├║c ─æ├│, mß╗Öt t├Āu c├Īc xuß║źt ph├Īt tß╗½ A, chß║Īy theo hŲ░ß╗øng \(N{30^ \circ }E\) vß╗øi vß║Łn tß╗æc 50 km/h. Sau 2 giß╗Ø, hai t├Āu c├Īch nhau bao nhi├¬u ki l├┤ m├®t?
A. 110 km
B. 112 km
C. 111,4 km
D. 110,5 km
-
Giß║Żi b├Āi 3.37 trang 43 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Mß╗Öt ngŲ░ß╗Øi ─æß╗®ng tr├¬n ─æ├Āi quan s├Īt ─æß║Ęt ß╗¤ cuß╗æi mß╗Öt ─æŲ░ß╗Øng ─æua thß║│ng. ß╗× ─æß╗Ö cao 6m so vß╗øi mß║Ęt ─æŲ░ß╗Øng ─æua, tß║Īi mß╗Öt thß╗Øi ─æiß╗ām ngŲ░ß╗Øi ─æ├│ nh├¼n hai vß║Łn ─æß╗Öng vi├¬n A v├Ā B dŲ░ß╗øi c├Īc g├│c tŲ░ŲĪng ß╗®ng l├Ā \({60^ \circ }\) v├Ā \({30^ \circ },\) so vß╗øi phŲ░ŲĪng nß║▒m ngang (H.3.6). Khoß║Żng c├Īch giß╗»a hai vß║Łn ─æß╗Öng vi├¬n A v├Ā B (l├Ām tr├▓n ─æß║┐n h├Āng ─æŲĪn vß╗ŗ, theo ─æŲĪn vß╗ŗ m├®t) tß║Īi thß╗Øi ─æiß╗ām ─æ├│ l├Ā:
A. \(8m.\)
B. \(7m.\)
C. \(6m.\)
D. \(9m.\)
-
Giß║Żi b├Āi 3.38 trang 43 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Cho g├│c t├╣ \(\alpha \) c├│ \(\sin \alpha = \frac{1}{3}.\)
a) T├Łnh \(cos\alpha ,\,\,\tan \alpha ,\,\,\cot \alpha .\)
b) T├Łnh gi├Ī trß╗ŗ cß╗¦a c├Īc biß╗āu thß╗®c:
\(\) \(\begin{array}{l}A = \sin \alpha .\cot \left( {{{180}^ \circ } - \alpha } \right) + \cos \left( {{{180}^ \circ } - \alpha } \right).\cot \left( {{{90}^ \circ } - \alpha } \right).\\B = \frac{{3\left( {\sin \alpha + \sqrt 2 .\cos \alpha } \right) - 2}}{{\sin \alpha - \sqrt 2 .\cos \alpha }}.\end{array}\)
-
Giß║Żi b├Āi 3.39 trang 43 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Cho \(\sin {15^ \circ } = \frac{{\sqrt 6 - \sqrt 2 }}{4}.\)
a) T├Łnh \(\sin {75^ \circ },\,\,\cos {105^ \circ },\,\,\tan {165^ \circ }.\)
b) T├Łnh gi├Ī trß╗ŗ cß╗¦a biß╗āu thß╗®c
\(A = \sin {75^ \circ }.\cos {165^ \circ } + \cos {105^ \circ }.\sin {165^ \circ }.\)
-
Giß║Żi b├Āi 3.40 trang 43 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Cho tam gi├Īc \(ABC\) c├│ \(AB = 1,\,\,BC = 2,\,\,\widehat {ABC} = {60^ \circ }.\) T├Łnh ─æß╗Ö d├Āi cß║Īnh v├Ā sß╗æ ─æo c├Īc g├│c c├▓n lß║Īi cß╗¦a tam gi├Īc
-
Giß║Żi b├Āi 3.41 trang 44 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Cho tam gi├Īc \(ABC\) c├│ \(c = 1,\,\,a = 2,\,\,\widehat B = {120^ \circ }.\)
a) T├Łnh \(b,\,\,\widehat A,\,\,\widehat C.\)
b) T├Łnh diß╗ćn t├Łch cß╗¦a tam gi├Īc
c) T├Łnh ─æß╗Ö d├Āi ─æŲ░ß╗Øng cao kß║╗ tß╗½ \(B\) cß╗¦a tam gi├Īc
-
Giß║Żi b├Āi 3.42 trang 44 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Cho tam gi├Īc \(ABC\) c├│ \(a = 3,\,\,b = 5,\,\,c = 7.\)
a) T├Łnh c├Īc g├│c cß╗¦a tam gi├Īc, l├Ām tr├▓n ─æß║┐n ─æß╗Ö.
b) T├Łnh b├Īn k├Łnh ─æŲ░ß╗Øng tr├▓n nß╗Öi tiß║┐p v├Ā ─æŲ░ß╗Øng tr├▓n ngoß║Īi tiß║┐p cß╗¦a tam gi├Īc.
-
Giß║Żi b├Āi 3.43 trang 44 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Cho tam gi├Īc \(ABC\) c├│ \(\widehat B = {45^ \circ },\,\,\widehat C = {15^ \circ },\,\,b = \sqrt 2 .\) T├Łnh \(a,\,\,{h_a}.\)
-
Giß║Żi b├Āi 3.44 trang 44 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Cho tam gi├Īc \(ABC\) c├│ \(c = 5,\,\,a = 8,\,\,\widehat B = {60^ \circ }.\)
a) T├Łnh \(b\) v├Ā c├Īc g├│c cß╗¦a \(A,C\) (sß╗æ ─æo c├Īc g├│c l├Ām tr├▓n ─æß║┐n h├Āng ─æŲĪn vß╗ŗ, theo ─æŲĪn vß╗ŗ ─æß╗Ö).
b) T├Łnh ─æß╗Ö d├Āi ─æŲ░ß╗Øng cao kß║╗ tß╗½ \(B.\)
c) T├Łnh ─æß╗Ö d├Āi trung tuyß║┐n kß╗ā tß╗½ \(A.\)
-
Giß║Żi b├Āi 3.45 trang 44 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Cho tam gi├Īc \(ABC\) c├│ \(\widehat B = {15^ \circ },\,\,\widehat C = {30^ \circ },\,\,c = 2.\)
a) T├Łnh sß╗æ ─æo g├│c \(A\) v├Ā ─æß╗Ö d├Āi c├Īc cß║Īnh \(a,b.\)
b) T├Łnh diß╗ćn t├Łch v├Ā b├Īn k├Łnh ─æŲ░ß╗Øng tr├▓n ngoß║Īi tiß║┐p cß╗¦a tam gi├Īc.
c) Lß║źy ─æiß╗ām \(D\) thuß╗Öc cß║Īnh \(AB\) sao cho \(\widehat {BCD} = \widehat {DCA}\) (tß╗®c \(CD\) l├Ā tia ph├ón gi├Īc cß╗¦a \(\widehat {BCA}\)). T├Łnh ─æß╗Ö d├Āi \(CD.\)
-
Giß║Żi b├Āi 3.46 trang 44 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Tr├¬n biß╗ān, mß╗Öt t├Āu c├Ī xuß║źt ph├Īt tß╗½ cß║Żng A, chß║Īy vß╗ü phŲ░ŲĪng ─æ├┤ng 15 km tß╗øi B, rß╗ōi chuyß╗ān sang hŲ░ß╗øng \(E{30^ \circ }S\) chß║Īy tiß║┐p 20 km nß╗»a tß╗øi ─æß║Żo C.
a) T├Łnh khoß║Żng c├Īch tß╗½ A ─æß║┐n C (l├Ām tr├▓n ─æß║┐n h├Āng ─æŲĪn vß╗ŗ, theo ─æŲĪn vß╗ŗ ki l├┤ m├®t).
b) X├Īc ─æß╗ŗnh hŲ░ß╗øng tß╗½ A tß╗øi C (l├Ām tr├▓n ─æß║┐n h├Āng ─æŲĪn vß╗ŗ, theo ─æŲĪn vß╗ŗ ─æß╗Ö).
-
Giß║Żi b├Āi 3.47 trang 44 SBT To├Īn 10 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Tr├¬n sŲ░ß╗Øn ─æß╗ōi, vß╗øi ─æß╗Ö dß╗æc \(12\% \) (─æß╗Ö dß╗æc cß╗¦a sŲ░ß╗Øn ─æß╗ōi ─æŲ░ß╗Żc t├Łnh bß║▒ng tang cß╗¦a mß╗Öt g├│c tß║Īo bß╗¤i sŲ░ß╗Øn ─æß╗ōi vß╗øi phŲ░ŲĪng nß║▒m ngang) c├│ mß╗Öt c├óy cao mß╗Źc thß║│ng ─æß╗®ng. ß╗× ph├Ła ch├ón ─æß╗ōi, c├Īch gß╗æc c├óy 30m, ngŲ░ß╗Øi ta nh├¼n ngß╗Źn c├óy dŲ░ß╗øi mß╗Öt g├│c \({45^ \circ }\) so vß╗øi phŲ░ŲĪng nß║▒m ngang. T├Łnh chiß╗üu cao cß╗¦a c├óy ─æ├│ (l├Ām tr├▓n ─æß║┐n h├Āng ─æŲĪn vß╗ŗ, theo ─æŲĪn vß╗ŗ m├®t).

.JPG)
.JPG)