Giải bài tập Toán 10 Chân trời sáng tạo Bài 2: Hàm số bậc hai

Khai triển biểu thức của các hàm số sau và sắp xếp theo thứ tự lũy thừa của x giảm dần (nếu có thể). Hàm số nào có lũy thừa bậc cao nhất của x là bậc hai?

a) \(y = 2x(x - 3)\)

b) \(y = x({x^2} + 2) - 5\)

c) \(y =  - 5(x + 1)(x - 4)\)

Hàm số nào trong các hàm số được cho ở Hoạt động khám phá 1 là hàm số bậc hai?

a) Xét hàm số\(y = f(x) = {x^2} - 8x + 19 = {(x - 4)^2} + 3\) có bảng giá trị:

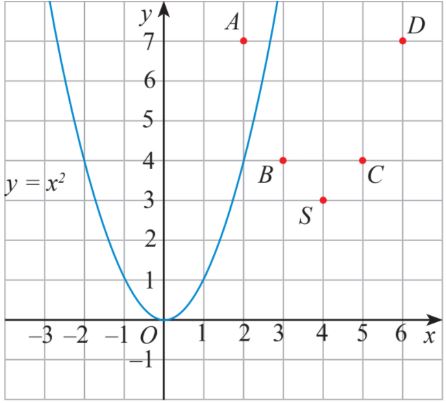
Trên mặt phẳng tọa độ, ta có các điểm \((x;f(x))\) với x thuộc bảng giá trị đã cho (hình 1).

Hãy vẽ đường cong đi qua các điểm A, B, S, C, D và nêu nhận xét về hình dạng của đường cong này so với đồ thị hàm số \(y = {x^2}\) trên Hình 1.

b) Tương tự xét hàm số \(y = g(x) =  - {x^2} + 8x - 13 =  - {(x - 4)^2} + 3\) có bảng giá trị:

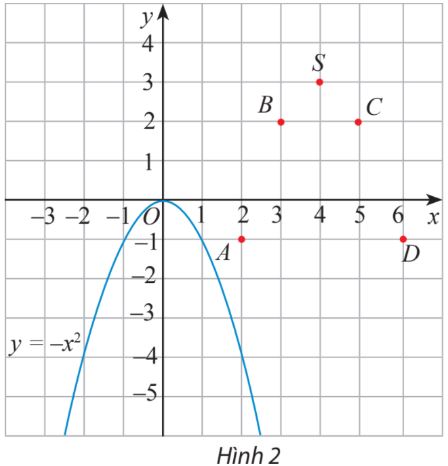
Trên mặt phẳng tọa độ, ta có các điểm \((x;f(x))\) với x thuộc bảng giá trị đã cho (hình 2).

Hãy vẽ đường cong đi qua các điểm A, B, S, C, D và nêu nhận xét về hình dạng của đường cong này so với đồ thị hàm số \(y =  - {x^2}\) trên Hình 2.

Vẽ đồ thị hàm số \(y = {x^2} - 4x + 3\) rồi so sánh đồ thị hàm số này với đồ thị hàm số trong Ví dụ 2z. Nếu nhận xét về hai đồ thị này.

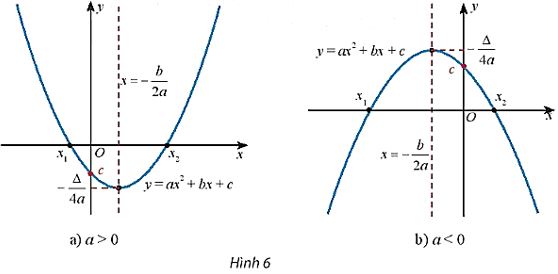
Từ đồ thị hàm số bậc hai cho ở hai hình sau, tìm khoảng đồng biến và nghịch biến của hàm số trong mỗi trường hợp.

Tìm khoảng đồng biến, khoảng nghịch biến của hàm số \(y = 2{x^2} - 6x + 11.\) Hàm số này có thể đạt giá trị bằng -1 không? Tại sao?

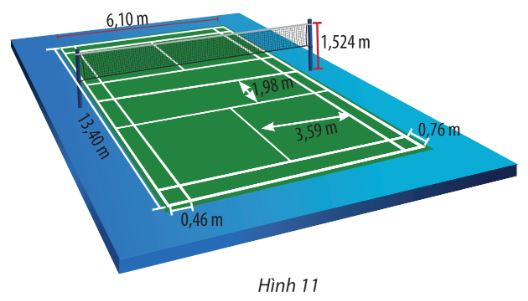
Trong bài toán ứng dụng, khi chơi trên sân cầu lông đơn, các lần phát cầu với thông tin như sau có được xem là hợp lệ không? (Các thông tin không được đề cập thì vẫn giữ như trong giả thiết bài toán trên)

a) Vận tốc xuất phát của cầu là 12 m/s

b) Vị trí phát cầu cách mặt đất 1,3 m.

Lưu ý: Các thông số về sân cầu lông đơn được cho trong Hình 11.

Hàm số nào sau đây là hàm số bậc hai?

a) \(y = 9{x^2} + 5x + 4\)

b) \(y = 3{x^3} + 2x + 1\)

c) \(y =  - 4{(x + 2)^2} + 2(2{x^3} + 1) + x + 4\)

d) \(y = 5{x^2} + \sqrt x  + 2\)

Tìm điều kiện của m để mỗi hàm số sau là hàm số bậc hai:

a) \(y = m{x^4} + (m + 1){x^2} + x + 3\)

b) \(y = (m - 2){x^3} + (m - 1){x^2} + 5\)

Lập bảng biến thiên của hàm số \(y = {x^2} + 2x + 3.\) Hàm số này có giá trị lớn nhất hay giá trị nhỏ nhất? Tìm giá trị đó.

Cho hàm số bậc hai \(y = f(x) = a{x^2} + bx + c\) có \(f(0) = 1,f(1) = 2,f(2) = 5.\)

a) Hãy xác định giá trị của các hệ số \(a,b\) và \(c.\)

b) Xác định tập giá trị và khoảng biến thiên của hàm số.

Cho hàm số \(y = 2{x^2} + x + m\). Hãy xác định giá trị của m để hàm số đạt giá trị nhỏ nhất bằng 5.

Vẽ đồ thị các hàm số sau:

a) \(y = 2{x^2} + 4x - 1\)

b) \(y =  - {x^2} + 2x + 3\)

c) \(y =  - 3{x^2} + 6x\)

d) \(y = 2{x^2} - 5\)

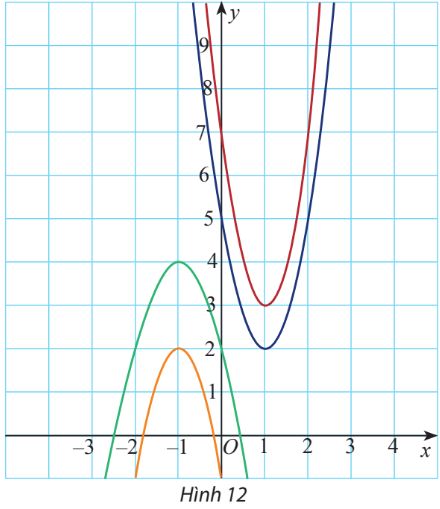
Hãy xác định đúng đồ thị của mỗi hàm số sau trên Hình 12.

\(\begin{array}{l}({P_1}):y =  - 2{x^2} - 4x + 2;\\({P_2}):y = 3{x^2} - 6x + 5;\\({P_3}):y = 4{x^2} - 8x + 7;\\({P_4}):y =  - 3{x^2} - 6x - 1.\end{array}\)

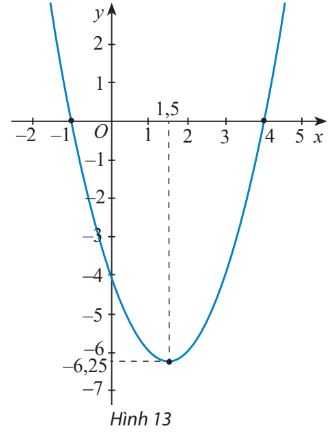
Tìm công thức của hàm số bậc hai có đồ thị như Hình 13.

Chiếc cầu dây văng một nhịp được thiết kế hai bên thành cầu có dạng parabol và được cố định bằng các dây cáp song song.

Dựa vào bản vẽ ở Hình 14, hãy tính chiều dài tổng cộng của các dây cáp dọc ở hai mặt bên. Biết:

-  Dây dài nhất là 5 m, dây ngắn nhất là 0,8 m. Khoảng cách giữa các dây bằng nhau.

-  Nhịp cầu dài 30 m.

-  Cần tính thêm 5% chiều dài mỗi sợi dây cáp để neo cố định.

Hàm số nào trong các hàm sau đây không phải là hàm số bậc hai?

a) \(y = 3{x^2} + x - \sqrt 3 \)

b) \(y = {x^2} + \left| {x + 1} \right|\)

c) \(y = \left\{ \begin{array}{l}{x^2} + 1{\rm{         với }}x \ge 0\\ - 2{x^2} - x{\rm{   với }}x < 0\end{array} \right.\)

d) \(y = 2\left( {{x^2} + 1} \right) + 3x - 1\)

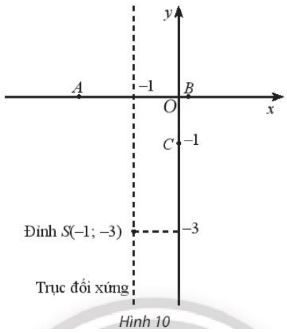
Cho hàm số bậc hai có đồ thị là parabol có đỉnh S , đi qua các điểm A, B, \(C\left( {0; - 1} \right)\) được cho trong hình 10

a) Vẽ đồ thị hàm số đã cho

b) Tìm tập giá trị của hàm số và chỉ ra các khoảng biến thiên của hàm số

Tìm công thức của hàm số có đồ thị vẽ được ở bài tập 2

Cho hàm số bậc hai có đồ thị là parabol có đỉnh S , đi qua các điểm A, B, \(C\left( {0; - 1} \right)\) được cho trong hình 10

Tìm công thức hàm số bậc hai biết:

a) Đồ thị hàm số đi qua 3 điểm \(A\left( {1; - 3} \right),B\left( {0; - 2} \right),C\left( {2; - 10} \right)\)

b) Đồ thị hàm số có trục đối xứng là đường thẳng \(x = 3\), cắt trục tung tại điểm có tung độ bằng \( - 16\) và một trong hai giao điểm với trục hoành có hoành độ là \( - 2\)

Tìm khoảng biến thiên và tập giá trị của các hàm số sau:

a) \(y = f\left( x \right) =  - 2{x^2} - 4x + 7\)   

b) \(y = f\left( x \right) = {x^2} - 6x + 1\) 

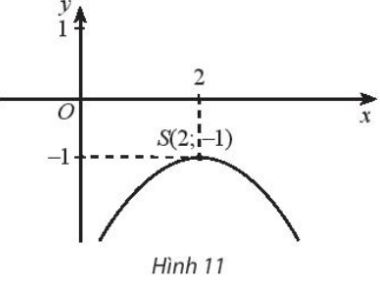
Tìm tập xác định, giá trị lớn nhất của hàm số, tập giá trị và các khoảng biến thiên của hàm số biết đồ thị hàm số là một parabol có đỉnh S như hình 11

Giả sử hàm số bậc hai mô phỏng vòm phía trong một trụ của cầu nhật tân là:

                             \(y = f\left( x \right) =  - \frac{{187}}{{856}}{x^2} + \frac{{8041}}{{856}}x\) (đơn vị đo: mét)

a) Hãy tính chiêu dài đoạn dây dọi sử dụng nếu khoảng cách từ chân của trụ cầu đễn quả nặng là 30 cm

b) Hãy tính khoảng cách từ chân trụ cầu đến quả nặng nếu biết chiều dài đoạn dây dọi sử dụng là 15 m