Giải bài 3 trang 55 SBT Toán 10 Chân trời sáng tạo tập 1
Tìm công thức của hàm số có đồ thị vẽ được ở bài tập 2
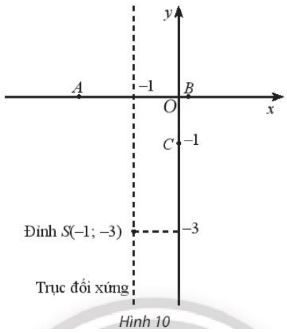
Cho hàm số bậc hai có đồ thị là parabol có đỉnh S , đi qua các điểm A, B, \(C\left( {0; - 1} \right)\) được cho trong hình 10
Hướng dẫn giải chi tiết Bài 3
Phương pháp giải
Bước 1: Đặt công thức của hàm số theo dạng tổng quát \(y = a{x^2} + bx + c\)
Bước 2: Thay các điểm mà hàm số đi qua và sử dụng các tính chất của hàm số bậc hai để xác định a, b, c
Lời giải chi tiết
Gọi công thức tổng quát của hàm số bậc hai có dạng \(y = a{x^2} + bx + c\) với a, b, c là các số thực và a khác 0
Đồ thị hàm số có đỉnh \(S\left( { - 1; - 3} \right)\) nên ta có : \( - 1 = - \frac{b}{{2a}} \Rightarrow b = 2a\) (1)
Mặt khác đồ thị hàm số cắt trục tung tại điểm \(C\left( {0; - 1} \right)\)nên \(c = - 1\) (2)
Đồ thị hàm số đi qua điểm S nên thay tọa độ điểm S vào ta được phương trình:
\( - 3 = a{\left( { - 1} \right)^2} + b\left( { - 1} \right) + c \Rightarrow a - b + c = - 3\) (3)
Từ (1), (2) và (3) ta tìm được \(a = 2,b = 4\) và \(c = - 1\)
Vậy hàm số cần tìm có công thức là \(y = 2{x^2} + 4x - 1\)
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải bài 1 trang 54 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 55 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 55 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 55 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 55 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 56 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST