Hoạt động khám phá 3 trang 52 SGK Toán 10 Chân trời sáng tạo tập 1
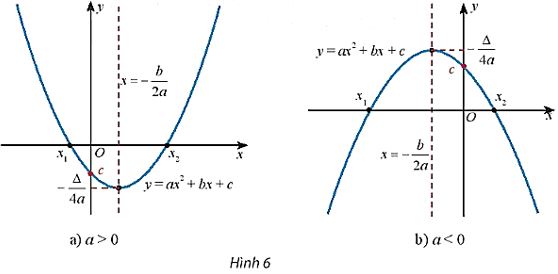
Từ đồ thị hàm số bậc hai cho ở hai hình sau, tìm khoảng đồng biến và nghịch biến của hàm số trong mỗi trường hợp.
Hướng dẫn giải chi tiết Hoạt động khám phá 3
Phương pháp giải
Quan sát đồ thị hàm số trên các khoảng \(( - \infty ; - \frac{b}{{2a}})\) và \(( - \frac{b}{{2a}}; + \infty )\)
Trên (a’; b’): đồ thị có dạng đi lên từ trái sang phải thì hàm số đó đồng biến trên (a’;b’).
Trên (c; d): đồ thị có dạng đi xuống từ trái sang phải thì hàm số đó nghịch biến trên (c;d).
Lời giải chi tiết
a)
Trên \(( - \infty ; - \frac{b}{{2a}})\) đồ thị có dạng đi xuống từ trái sang phải nên hàm số đó nghịch biến trên \(( - \infty ; - \frac{b}{{2a}})\)
Trên \(( - \frac{b}{{2a}}; + \infty )\) đồ thị có dạng đi lên từ trái sang phải nên hàm số đó đồng biến trên \(( - \frac{b}{{2a}}; + \infty )\)
Vậy hàm số có khoảng đồng biến là \(( - \frac{b}{{2a}}; + \infty )\), khoảng nghịch biến là \(( - \infty ; - \frac{b}{{2a}})\)
b)
Trên \(( - \infty ; - \frac{b}{{2a}})\) đồ thị có dạng đi lên từ trái sang phải nên hàm số đó đồng biến trên \(( - \infty ; - \frac{b}{{2a}})\)
Trên \(( - \frac{b}{{2a}}; + \infty )\) đồ thị có dạng đi xuống từ trái sang phải nên hàm số đó nghịch biến trên \(( - \frac{b}{{2a}}; + \infty )\)
Vậy hàm số có khoảng đồng biến là \(( - \infty ; - \frac{b}{{2a}})\), khoảng nghịch biến là \(( - \frac{b}{{2a}}; + \infty )\)
-- Mod Toán 10 HỌC247
-


Cho hàm số: \(y = (x - 3)^2\). Không vẽ đồ thị, tìm đỉnh của parabol, trục đối xứng, hướng bề lõm.
bởi Suong dem
 28/08/2022
Theo dõi (0) 1 Trả lời
28/08/2022
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Hoạt động khám phá 2 trang 49 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 2 trang 52 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 3 trang 53 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Vận dụng trang 55 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 56 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 56 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 56 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 56 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 56 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 56 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 56 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 57 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 9 trang 57 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 54 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 55 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 55 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 55 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 55 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 55 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 56 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST