Giải bài 5 trang 55 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST

Phương pháp giải

Xác định toạ độ đỉnh

Vẽ bảng biến thiên

Từ bảng biến thiên kết luận: hàm số đồng biến, nghịch biến, tập giá trị

Lời giải chi tiết

a) Hàm số \(y = f\left( x \right) =  - 2{x^2} - 4x + 7\) có \(a =  - 2 < 0\) và tọa độ đỉnh gồm \({x_S} =  - \frac{b}{{2a}} =  - \frac{{ - 4}}{{2.\left( { - 2} \right)}} =  - 1,{y_S} =  - 2.{\left( { - 1} \right)^2} - 4.\left( { - 1} \right) + 7 = 9\)

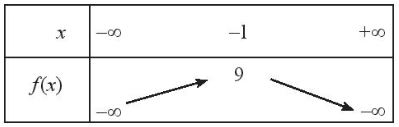
Ta có bảng biến thiên sau

Vậy hàm số đồng biến trên \(\left( { - \infty ;-1} \right)\) và nghịch biến \(\left( -1; + \infty \right)\)

Hàm số có tập giá trị \(T = \left( { - \infty ; 9} \right]\)

b) Hàm số \(y = f\left( x \right) =  {x^2} - 6x + 1\) có \(a =  1> 0\) và tọa độ đỉnh gồm \({x_S} =  - \frac{b}{{2a}} =  - \frac{{ -6}}{{2.1}} =  3,{y_S} = {3^2} - 6.3 + 1 = -8\)

Ta có bảng biến thiên sau

Vậy hàm số nghịch biến trên \(\left( { - \infty ;3} \right)\) và đồng biến \(\left( 3; + \infty \right)\)

Hàm số có tập giá trị \(T = \left( {-8; + \infty } \right]\)

-- Mod Toán 10 HỌC247