Giải bài 5 trang 56 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST

Phương pháp giải

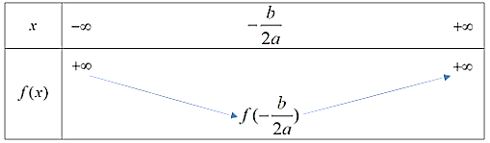
Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}};{y_S} = f(\frac{{ - b}}{{2a}})\)

\(a = 2 > 0\) nên ta có bảng biến thiên sau:

Hàm số đạt giá trị nhỏ nhất bằng \(f( - \frac{b}{{2a}})\) tại \(x =  - \frac{b}{{2a}}.\)

=>  Tìm m để \(f( - \frac{b}{{2a}}) = 5\)

Lời giải chi tiết

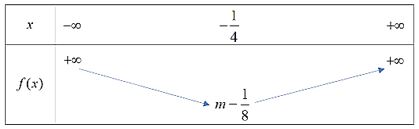
Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 1}}{{2.2}} =  - \frac{1}{4};{y_S} = f( - \frac{1}{4}) = 2{\left( { - \frac{1}{4}} \right)^2} + \left( { - \frac{1}{4}} \right) + m = m - \frac{1}{8}\)

Ta có: \(a = 2 > 0\), hàm số có bảng biến thiên dạng:

Hàm số đạt giá trị nhỏ nhất bằng \(m - \frac{1}{8} = 5 \Leftrightarrow m = \frac{{41}}{8}.\)

Vậy \(m = \frac{{41}}{8}\) thì hàm số đạt giá trị nhỏ nhất bằng 5.

-- Mod Toán 10 HỌC247