Hướng dẫn Giải bài tập Toán 10 Chân trời sáng tạo Bài tập cuối chương 7 giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
Giải bài 1 trang 18 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Xét dấu của các tam thức bậc hai sau:
a) \(f\left( x \right) = 6{x^2} + 41x + 44\)
b) \(g\left( x \right) = - 3{x^2} + x - 1\)
c) \(h\left( x \right) = 9{x^2} + 12x + 4\)
-
Giải bài 2 trang 18 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải các bất phương trình sau:
a) \(7{x^2} - 19x - 6 \ge 0\)
b) \( - 6{x^2} + 11x > 10\)
c) \(3{x^2} - 4x + 7 > {x^2} + 2x + 1\)
d) \({x^2} - 10x + 25 \le 0\)
-
Giải bài 3 trang 18 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
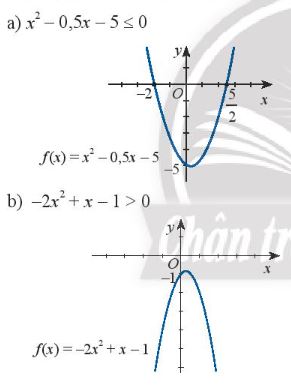
Dựa vào đồ thị của hàm số bậc hai được cho, hãy giải các bất phương trình sau:
-
Giải bài 4 trang 18 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải các phương trình sau:
a) \(\sqrt {{x^2} - 7x} = \sqrt { - 9{x^2} - 8x + 3} \)
b) \(\sqrt {{x^2} + x + 8} - \sqrt {{x^2} + 4x + 1} = 0\)
c) \(\sqrt {4{x^2} + x - 1} = x + 1\)
d) \(\sqrt {2{x^2} - 10x - 29} = \sqrt {x - 8} \)
-
Giải bài 5 trang 18 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Một tam giác vuông có một cạnh góc vuông ngắn hơn cạnh huyền 8 cm. Tính độ dài của cạnh huyền, biết chu vi của tam giác bằng 30 cm.
-
Giải bài 6 trang 18 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Một quả bóng được bắn thẳng lên từ độ cao 2 m với vận tốc ban đầu là 30 m/s. Khoảng cách quả bóng so với mặt đất t giây được cho bởi hàm số:
\(h\left( t \right) = - 4,9{t^2} + 30t + 2\)
với \(h\left( t \right)\) tính bằng đơn vị mét. Hỏi quả bóng nằm ở độ cao trên 40 m trong thời gian bao lâu? Làm tròn kết quả đến hàng phần mười.
-
Giải bài 7 trang 18 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Một chú cá heo nhảy lên khỏi mặt nước sau t giây được cho bởi hàm số \(h\left( t \right) = - 4,9{t^2} + 9,6t\)
Tính khoảng thời gian cá heo ở trên không.
-
Giải bài 8 trang 18 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Lợi nhuận một tháng \(p\left( x \right)\) của một quán ăn phụ thuộc vào giá trung bình x của các món ăn theo công thức \(p\left( x \right) = - 30{x^2} + 2100x - 15000\), với đơn vị tính bằng nghìn đồng. Nếu muốn lợi nhuận không dưới 15 triệu đồng một tháng thì giá bán trung bình của các món ăn cần nằm trong khoảng nào?
-
Giải bài 9 trang 18 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Quỹ đạo của một quả bóng được mô tả bằng hàm số \(y = f\left( x \right) = - 0,03{x^2} + 0,4x + 1,5\)
với y (tính bằng mét) là độ cao của quả bóng so với mặt đất khi độ dịch chuyển theo phương ngang của bóng là x (tính bằng mét). Để quả bóng có thể ném được qua lưới cao 2 m, người ta phải đứng cách lưới bao xa? Làm tròn kết quả đến hàng phần mười
-
Giải bài 1 trang 19 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Tam thức bậc hai nào có biệt thức \(\Delta = 1\) và hai nghiệm là:\({x_1} = \frac{3}{2}\) và \({x_2} = \frac{7}{4}\)?
A. \(8{x^2} - 26x + 21\) B. \(4{x^2} - 13x + \frac{{21}}{2}\)
C. \(4{x^2} + 4x - 15\) D. \(2{x^2} - 7x + 6\)
-
Giải bài 2 trang 19 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Tam thức bậc hai nào dương với mọi \(x \in \mathbb{R}\)?
A. \(2{x^2} - 4x + 2\)
B. \(3{x^2} + 6x + 2\)
C. \( - {x^2} + 2x + 3\)
D. \(5{x^2} - 3x + 1\)
-
Giải bài 3 trang 19 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Khẳng định nào sau đây đúng với tam thức bậc hai \(f\left( x \right) = 10{x^2} - 3x - 4\)?
A. \(f\left( x \right) > 0\) với mọi x không thuộc khoảng \(\left( { - 1;1} \right)\)
B. \(f\left( x \right) < 0\) với mọi x thuộc khoảng \(\left( { - 1;1} \right)\)
C. \(f\left( x \right) \ge 0\) với mọi x thuộc khoảng \(\left( { - \frac{1}{2};\frac{5}{4}} \right)\)
D. Các khẳng định trên đều sai
-
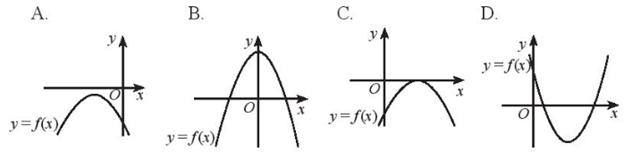
Giải bài 4 trang 19 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Trong trường hợp nào tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\) có \(\Delta > 0\) và \(a < 0\)?
-
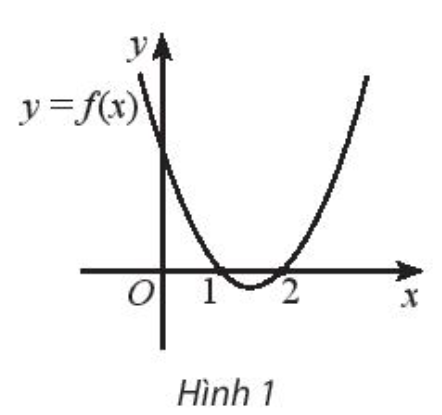
Giải bài 5 trang 20 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Cho đồ thị của hàm số bậc hai \(y = f\left( x \right)\) như hình 1. Tập nghiệm của bất phương trình \(f\left( x \right) \ge 0\) là:
A. \(\left( {1;2} \right)\)
B. \(\left[ {1;2} \right]\)
C. \(\left( { - \infty ;1} \right) \cup \left( {2; + \infty } \right)\)
D. \(\left( { - \infty ;1} \right] \cup \left[ {2; + \infty } \right)\)
-
Giải bài 6 trang 20 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Bất phương trình nào có tập nghiệm là \(\left( {2;5} \right)\)?
A. \({x^2} - 7x + 10 > 0\)
B. \({x^2} - 7x + 10 < 0\)
C. \({x^2} + 13x - 30 > 0\)
D. \({x^2} + 13x - 30 < 0\)
-
Giải bài 7 trang 20 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Tập xác định của hàm số \(y = \frac{1}{{\sqrt {9{x^2} - 3x - 2} }} + \sqrt {3 - x} \)là:
A. \(\left( { - \infty ; - \frac{1}{3}} \right) \cup \left( {\frac{2}{3}; + \infty } \right)\)
B. \(\left( { - \infty ; - \frac{1}{3}} \right) \cup \left( {\frac{2}{3};3} \right]\)
C. \(\left( { - \infty ; - \frac{1}{3}} \right) \cup \left( {3; + \infty } \right)\)
D. \(\left( { - \frac{1}{3};3} \right]\)
-
Giải bài 8 trang 20 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Với giá trị nào của tham số m thì phương trình \(\left( {2m + 6} \right){x^2} + 4mx + 3 = 0\) có hai nghiệm phân biệt?
A. \(m < - \frac{3}{2}\) hoặc \(m > 3\)
B. \( - \frac{3}{2} < m < 3\)
C. \(m < - 3\) hoặc \( - 3 < m < - \frac{3}{2}\)hoặc \(m > 3\)
D. \( - 3 < m < - \frac{3}{2}\)hoặc \(m > 3\)
-
Giải bài 9 trang 20 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giá trị nào là nghiệm của phương trình \(\sqrt {{x^2} + x + 11} = \sqrt { - 2{x^2} - 13x + 16} \)?
A. \(x = - 5\)
B. \(x = \frac{1}{3}\)
C. Cả hai câu A, B đều đúng
D. Cả hai câu A, B đều sai
-
Giải bài 10 trang 20 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Khẳng định nào đúng với phương trình \(\sqrt {2{x^2} - 3x - 1} = \sqrt {3{x^2} - 2x - 13} \)
A. Phương trình có hai nghiệm phân biệt cùng dấu
B. Phương trình có hai nghiệm phân biệt trái dấu
C. Phương trình có một nghiệm
D. Phương trình vô nghiệm
-
Giải bài 11 trang 21 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Khẳng định nào đúng với phương trình \(\sqrt{5x^{2} + 27x + 36} = 2x + 5\)?
A. Phương trình có một nghiệm
B. Phương trình vô nghiệm
C. Tổng các nghiệm của phương trình là \( - 7\)
D. Các nghiệm của phương trình đều không bé hơn \( - \frac{5}{2}\)
-
Giải bài 12 trang 21 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
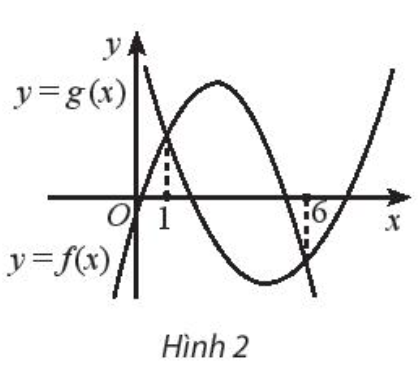
Cho đồ thị của hai hàm số bậc hai \(f\left( x \right) = a{x^2} + bx + c\) và \(g\left( x \right) = d{x^2} + ex + h\) như hình 2. Khẳng định nào đúng với phương trình \(\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + h} \)?
A. Phương trình có hai nghiệm phân biệt là \(x = 1\) và \(x = 6\)
B. Phương trình có một nghiệm là \(x = 1\)
C. Phương trình có một nghiệm là \(x = 6\)
D. Phương trình vô nghiệm
-
Giải bài 1 trang 21 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
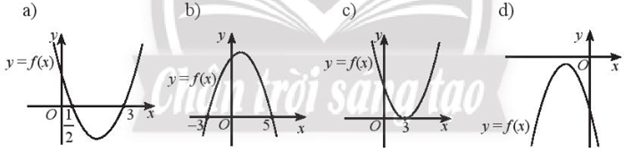
Dựa vào đồ thị của hàm số bậc hai \(y = f\left( x \right)\) sau đây, hãy xét dấu của tam thức bậc hai
-
Giải bài 2 trang 21 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Xét dấu của các tam thức bậc hai sau:
a) \(f\left( x \right) = - 7{x^2} + 44x - 45\)
b) \(f\left( x \right) = 4{x^2} + 36x + 81\)
c) \(f\left( x \right) = 9{x^2} - 6x + 3\)
d) \(f\left( x \right) = - 9{x^2} + 30x - 25\)
e) \(f\left( x \right) = - {x^2} - 4x + 3\)
g) \(f\left( x \right) = - 4{x^2} + 8x - 7\)
-
Giải bài 3 trang 21 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải các phương trình bậc hai sau:
a) \({x^2} - 10x + 24 \ge 0\)
b) \( - 4{x^2} + 28x - 49 \le 0\)
c) \({x^2} - 5x + 1 > 0\)
d) \(9{x^2} - 24x + 16 \le 0\)
e) \(15{x^2} - x - 2 < 0\)
g) \( - {x^2} + 8x - 17 > 0\)
h) \( - 25{x^2} + 10x - 1 < 0\)
i) \(4{x^2} + 4x + 7 \le 0\)
-
Giải bài 4 trang 22 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
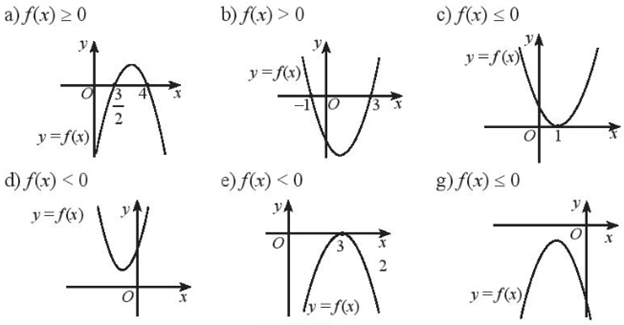
Dựa vào đồ thị của hàm số bậc hai được cho, hãy giải các bất phương trình sau:
-
Giải bài 5 trang 22 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải các phương trình sau:
a) \(\sqrt {3{x^2} + 7x - 1} = \sqrt {6{x^2} + 6x - 11} \)
b) \(\sqrt {{x^2} + 12x + 28} = \sqrt {2{x^2} + 14x + 24} \)
c) \(\sqrt {2{x^2} - 12x - 14} = \sqrt {5{x^2} - 26x - 6} \)
d) \(\sqrt {11{x^2} - 43x + 25} = - 3x + 4\)
e) \(\sqrt { - 5{x^2} - x + 35} = x + 5\)
g) \(\sqrt {11{x^2} - 64x + 97} = 3x - 11\)
-
Giải bài 6 trang 22 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Tìm tập xác định của các hàm số sau:
a) \(y = \sqrt { - {x^2} + 6x - 2} \)
b) \(y = \frac{{2x}}{{x - 2}} + \sqrt { - {x^2} + 3x - 2} \)
-
Giải bài 7 trang 22 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Tìm các giá trị của tham số m để:
a) \(f\left( x \right) = \left( {m - 3} \right){x^2} + 2mx - m\) là một tam thức bậc hai âm với mọi \(x \in \mathbb{R}\)
b) \(f\left( x \right) = \left( {m - 2} \right){x^2} + 2\left( {m + 3} \right)x + 5\left( {m - 3} \right)\) là một tam thức bậc hai có nghiệm
c) Phương trình \(2{x^2} + \left( {3m - 1} \right)x + 2\left( {m + 1} \right) = 0\) vô nghiệm
d) Bất phương trình \(2{x^2} + 2\left( {m - 3} \right)x + 3\left( {{m^2} - 3} \right) \ge 0\) có tập nghiệm là \(\mathbb{R}\)
-
Giải bài 8 trang 22 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Người ta thử nghiệm ném một quả bóng trên Mặt Trăng. Nếu quả bóng được ném lên từ độ cao \({h_0}\) (m) so với bề mặt của Mặt Trăng với vận tốc \({v_0}\) (m/s) thì độ cao của quả bóng sau t giây được cho bởi hàm số \(h\left( t \right) = - \frac{1}{2}g{t^2} + {v_0}t + {h_0}\) với \(g = 1,625\)m/s2 là gia tốc trọng trường của Mặt Trăng
a) Biết độ cao ban đầu của quả bóng vào các thời điểm 8 giây và 12 giây lần lượt là 30 m và 5 m, hãy tìm vận tốc ném; độ cao ban đầu của quả bóng và viết công thức \(h\left( t \right)\)
b) Quả bóng đạt độ cao trên 29 m trong bao nhiêu giây?
Lưu ý: Đáp số làm tròn đến hàng phần trăm.
-
Giải bài 9 trang 23 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Một người phát cầu qua lưới từu độ cao \({y_0}\) mét, nghiệm một góc \(\alpha \) so với phương ngang với vận tốc đầu \({v_0}\)
Phương trình chuyển động của quả cầu là:
\(y = \frac{{ - g}}{{2v_0^2{{\cos }^2}\alpha }}{x^2} + \tan \left( \alpha \right)x + {y_0}\) với\(g = 10\) m/s2
Viết phương trình chuyển động của quả cầu nếu \(\alpha = 45^\circ ,{y_0} = 0,3\) m và \({v_0} = 7,67\) m/s
b) Để cầu qua được lưới bóng cao 1,5 m thì người phát cầu phải đứng cách lưới bao xa?
Lưu ý: Đáp số làm tròn đến hàng phần trăm.
-
Giải bài 10 trang 23 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
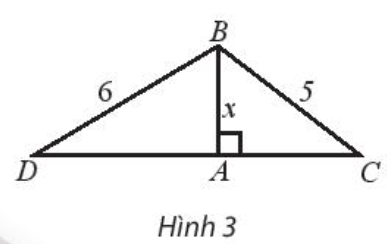
Cho tam giác ABC và ABD cùng vuông tại A như hình 3 có \(AB = x;BC = 5\) và \(BD = 6\)
a) Biểu diễn độ dài cạnh AC và AD theo x
b) Tìm x để chu vi của tam giác ABC là 12
c) Tìm x để \(AD = 2AC\)