Giải bài 2 trang 21 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST

Phương pháp giải

Để xét dâu tam thức bậc hai \(f(x) = a{x^2} + bx + c\left( {a \ne 0} \right)\), ta thực hiện các bước sau:

Bước 1: Tỉnh và xác định đâu của biệt thức \(\Delta \);

Bước 2: Xác định nghiệm của ƒ(x) (nếu có);

Bước 3: Xác định đâu của hệ sô a,

Bước 4: Xác định dâu của ƒ(x)

Lời giải chi tiết

a) \(f\left( x \right) =  - 7{x^2} + 44x - 45\) có \(\Delta  = 676 > 0\), hai nghiệm \({x_1} = \frac{9}{7};{x_2} = 5\) và có \(a =  - 7 < 0\)

Ta có bảng xét dấu \(f\left( x \right)\) như sau:

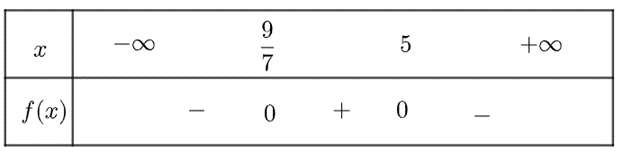
Vậy \(f\left( x \right)\) dương trong khoảng \(\left( {\frac{9}{7};5} \right)\) và âm trong khoảng \(\left( { - \infty ;\frac{9}{7}} \right) \cup \left( {5; + \infty } \right)\)

b) \(f\left( x \right) = 4{x^2} + 36x + 81\) có \(\Delta  = 0\), nghiệm kép \({x_1} = {x_2} =  - \frac{9}{2}\) và có \(a = 4 > 0\)

nên \(f\left( x \right)\) luôn dương với \(x \ne  - \frac{9}{2}\)

Vậy \(f\left( x \right)\) dương trong khoảng \(\mathbb{R}\backslash \left\{ { - \frac{9}{2}} \right\}\)

c) \(f\left( x \right) = 9{x^2} - 6x + 3\) có \(\Delta  =  - 72 < 0\) và\(a = 9 > 0\)

nên \(f\left( x \right)\) luôn dương với mọi \(x \in \mathbb{R}\)

Vậy \(f\left( x \right)\) dương với mọi x

d) \(f\left( x \right) =  - 9{x^2} + 30x - 25\)  có \(\Delta  = 0\), nghiệm kép \({x_1} = {x_2} = \frac{5}{3}\) và có \(a =  - 9 < 0\)

nên \(f\left( x \right)\) luôn âm với \(x \ne \frac{5}{3}\)

Vậy \(f\left( x \right)\) âm trong khoảng \(\mathbb{R}\backslash \left\{ {\frac{5}{3}} \right\}\)

e) \(f\left( x \right) = {x^2} - 4x + 3\) có \(\Delta  = 4 > 0\), hai nghiệm \({x_1} = 1;{x_2} = 3\) và có \(a = 1 > 0\)

Ta có bảng xét dấu \(f\left( x \right)\) như sau:

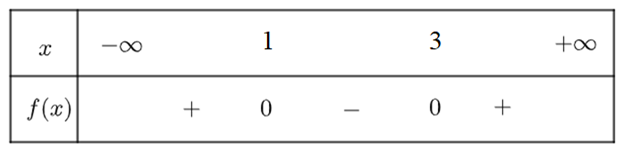
Vậy \(f\left( x \right)\) dương trên khoảng \(\left( { - \infty ;1} \right) \cup \left( {3; + \infty } \right)\) và âm trong khoảng \(\left( {1;3} \right)\)

g) \(f\left( x \right) =  - 4{x^2} + 8x - 7\) có có \(\Delta  =  - 48 < 0\) và\(a =  - 4 < 0\)

nên \(f\left( x \right)\) luôn âm với mọi \(x \in \mathbb{R}\)

-- Mod Toán 10 HỌC247