Hướng dẫn Giải bài tập Toán 10 Cánh Diều Chương 4 Bài 2 Giải tam giác giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
Câu hỏi khởi động trang 72 SGK Toán 10 Cánh diều tập 1 - CD
Từ xa xưa, con người đã cần đo đạc các khoảng cách mà không thể trực tiếp đo được. Chẳng hạn, để đo khoảng cách từ vị trí A trên bờ biển tới một hòn đảo (hay con tàu,...) trên biển, người xưa đã tìm ra một cách đo khoảng cách đó như sau:
Từ vị trí A, đo góc nghiêng \(\alpha\) so với bờ biển tới một vị trí C quan sát được trên đảo. Sau đó di chuyển dọc bờ biển đến vị trí B cách A một khoảng d và tiếp tục đo góc nghiêng \(\beta\) so với bờ biển tới vị trí C đã chọn (Hình 18).
Bằng cách giải tam giác ABC,họ tính được khoảng cách AC.Giải tam giác được hiểu như thế nào?
-
Hoạt động 1 trang 72 SGK Toán 10 Cánh diều tập 1 - CD
Cho tam giác ABC có \(AB = c, AC = b, \widehat A = \alpha \). Viết công thức tính BC theo \(b,c,\alpha \)
-
Hoạt động 2 trang 73 SGK Toán 10 Cánh diều tập 1 - CD
Cho tam giác ABC có \(AB = c, Ac = b, BC = a\). Viết công thức tính cos A.
-
Hoạt động 3 trang 73 SGK Toán 10 Cánh diều tập 1 - CD
Viết công thức định lí sin cho tam giác ABC.
-
Hoạt động 4 trang 73 SGK Toán 10 Cánh diều tập 1 - CD
Cho tam giác ABC có AB = c, AC = b, BC = a. Kẻ đường cao BH.
a) Tính BH theo c và sin A.
b) Tính diện tích S của tam giác ABC theo b, c, và sin A.
-
Luyện tập 1 trang 74 SGK Toán 10 Cánh diều tập 1 - CD
Cho tam giác ABC có AB = 12; \(\widehat B = {60^o}\); \(\widehat C = {45^o}\). Tính diện tích của tam giác ABC.
-
Hoạt động 5 trang 74 SGK Toán 10 Cánh diều tập 1 - CD
Cho tam giác ABC có BC = a, AC = b, AB =c và diện tích là S. (Hình 24).
a) Từ định lí cosin, chứng tỏ rằng:
\(\sin A = \frac{2}{{bc}}\sqrt {p(p - a)(p - b)(p - c)} \) ở đó \(p = \frac{{a + b + c}}{2}\)
b) Bằng cách sử dụng công thức \(S = \frac{1}{2}bc\sin A\),hãy chứng tỏ rằng: \(S = \sqrt {p(p - a)(p - b)(p - c)} \)
-
Luyện tập 2 trang 76 SGK Toán 10 Cánh diều tập 1 - CD
Từ trên nóc của một tòa nhà cao 18,5 m, bạn Nam quan sát một cái cây cách tòa nhà 30 m và dùng giác kế đo được góc lệch giữa phương quan sát gốc cây và phương nằm ngang là \({34^o}\), góc lệch giữa phương quan sát ngọn cây và phương nằm ngang là \({24^o}\). Biết chiều cao của chân giác kế là 1,5 m. Chiều cao của cái cây là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
-
Giải bài 1 trang 77 SGK Toán 10 Cánh diều tập 1 - CD
Cho tam giác ABC có \(BC = 12,CA = 15,\widehat C = {120^o}.\) Tính:
a) Độ dài cạnh AB.
b) Số đo các góc A, B.
c) Diện tích tam giác ABC.
-
Giải bài 2 trang 77 SGK Toán 10 Cánh diều tập 1 - CD
Cho tam giác ABC có \(AB = 5,BC = 7,\widehat A = {120^o}.\) Tính độ dài cạnh AC.
-
Giải bài 3 trang 77 SGK Toán 10 Cánh diều tập 1 - CD
Cho tam giác ABC có \(AB = 100,\widehat B = {100^o},\widehat C = {45^o}.\) Tính:
a) Độ dài các cạnh AC, BC
b) Diện tích tam giác ABC.
-
Giải bài 4 trang 77 SGK Toán 10 Cánh diều tập 1 - CD
Cho tam giác ABC có \(AB = 12,AC = 15,BC = 20.\) Tính:
a) Số đo các góc A, B, C.
b) Diện tích tam giác ABC.
-
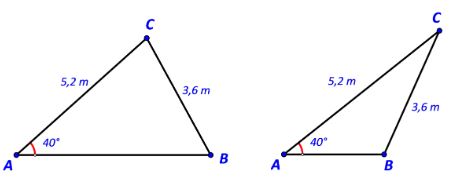
Giải bài 5 trang 77 SGK Toán 10 Cánh diều tập 1 - CD
Tính độ dài cạnh AB trong mỗi trường hợp sau:
-
Giải bài 6 trang 77 SGK Toán 10 Cánh diều tập 1 - CD
Để tính khoảng cách giữa hai địa điểm A và B mà ta không thể đi trực tiếp từ A đến B (hai địa điểm nằm ở hai bên bờ một hồ nước, một đầm lầy, …), người ta tiến hành như sau: Chọn một địa điểm C sao cho ta đo được các khoảng cách AC, CB và góc ACB. Sau khi đo, ta nhận được: AC = 1 km, CB = 800 m và \(\widehat {ACB} = {105^o}\) (Hình 31). Tính khoảng cách AB (làm tròn kết quả đến hàng phần mười đơn vị mét).
-
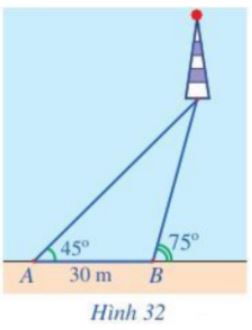
Giải bài 7 trang 77 SGK Toán 10 Cánh diều tập 1 - CD
Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là \({45^o}\) và \({75^o}\). Biết khoảng cách giữa hai vị trí A, B là 30 m (Hình 32). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
-
Giải bài 12 trang 79 SBT Toán 10 Cánh diều tập 1 - CD
Cho tam giác ABC có \(AB = 6,5cm,AC = 8,5cm,\widehat A = {125^0}\). Tính (làm tròn kết quả đến hàng phần mười theo đơn vị tương ứng):
a) Độ dài cạnh BC
b) Số đo các góc B, C
c) Diện tích tam giác ABC
-
Giải bài 13 trang 79 SBT Toán 10 Cánh diều tập 1 - CD
Cho tam giác ABC có \(BC = 50\)cm, \(\widehat B = {65^0},\widehat C = {45^0}\). Tính (làm tròn kết quả đến hàng phần mười theo đơn vị xentimet)
a) Độ dài cạnh AB, AC
b) Bán kính đường tròn ngoại tiếp tam giác ABC
-
Giải bài 14 trang 79 SBT Toán 10 Cánh diều tập 1 - CD
Cho tam giác ABC có \(AB = 5,AC = 8,BC = 9\). Tính (làm tròn kết quả đến hàng phần mười)
a) Số đo các góc A, B, C
b) Diện tích tam giác ABC
-
Giải bài 15 trang 79 SBT Toán 10 Cánh diều tập 1 - CD
Cho tam giác ABC có \(\widehat B = {60^0},BC = 8,AB + AC = 12\). Tính độ dài các cạnh AB, AC
-
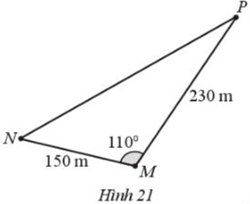
Giải bài 16 trang 79 SBT Toán 10 Cánh diều tập 1 - CD
Gia đình bạn An sở hữu một mảnh đất hình tam giác. Chiều dài của hàng rào MN là 150 m, chiều dài của hàng rào MP là 230 m. Góc giữa hai hàng rào MN và MP là 1100 (Hình 21)
a) Diện tích mảnh đất mà gia đình bạn An sở hữu là bao nhiêu mét vuông (làm tròn kết quả đến hàng phần mười)?
b) Chiều dài hàng rào NP là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
-
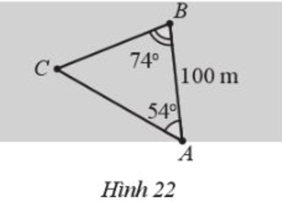
Giải bài 17 trang 80 SBT Toán 10 Cánh diều tập 1 - CD
Hai người A và B cùng quan sát một con tàu đang neo đậu ngoài khơi tại vị trí C. Người A đứng trên bờ biển, người B đứng trên một hòn đảo cách bờ một khoảng AB= 100 m. Hai người tiến hành đo đạc và thu được kết quả: \(\widehat {CAB} = {54^0},\widehat {CBA} = {74^0}\) (Hình 22). Hỏi con tàu cách hòn đảo bao xa (làm tròn kết quả đến hàng phần mười theo đơn vị mét)?
-
Giải bài 18 trang 80 SBT Toán 10 Cánh diều tập 1 - CD
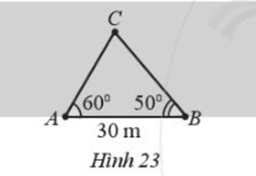
Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một con tàu C đang neo đậu ngoài khơi. Người đó tiến hành đo đạc và thu được kết quả: \(AB = 30m,\widehat {CAB} = {60^0},\widehat {CBA} = {50^0}\) (Hình 23). Tính khoảng cách từ vị trí A đến con tàu C(làm tròn kết quả đến hàng phần mười theo đơn vị mét)?
-
Giải bài 19 trang 80 SBT Toán 10 Cánh diều tập 1 - CD
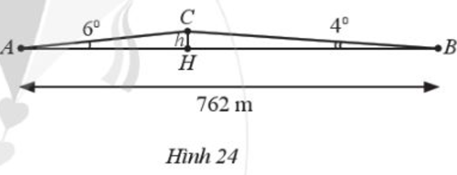
Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A) đến trường (điểm B) phải leo lên và xuống một con dốc (Hình 24). Cho biết đoạn thẳng AB dài 762 m, \(\widehat A = {6^0},\widehat B = {4^0}\)
a) Tính chiều cao h của con dốc theo đơn vị mét (làm tròn kết quả đến hàng đơn vị)
b) Hỏi bạn An đến trường lúc mấy giờ? Biết rằng tốc độ trung bình lên dốc là 4 km/h và tốc độ trung bình khi xuống dốc là 19 km/h.
-
Giải bài 20 trang 80 SBT Toán 10 Cánh diều tập 1 - CD
Quan sát cây cầu dây văng minh họa ở Hình 25
Tại trụ cao nhất, khoảng cách từ đỉnh trụ (vị trí A) tới chân trụ trên mặt cầu (vị trí H) là 150 m, độ dài dây văng dài nhất nối từ đỉnh trụ xuống mặt cầu (vị trí B) là 300 m, khoảng cách từ chân dây văng dài nhất tới chân trụ trên mặt cầu là 250 m (Hình 26). Tính độ dốc của cầu qua trụ nói trên (làm tròn kết quả đến hàng phần mười theo đơn vị độ).

-
Giải bài 21 trang 81 SBT Toán 10 Cánh diều tập 1 - CD
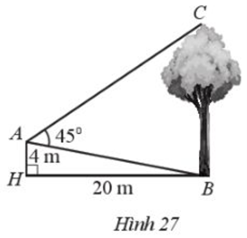
Một người đứng ở vị trí Atrên nóc một ngôi nhà cao 4 m đang quan sát đang quan sát một cây cao cách ngôi nhà 20 m và đo được \(\widehat {BAC} = {45^0}\) (Hình 27). Tính chiều cao của cây đó (làm tròn kết quả đến hàng phần mười theo đơn vị mét)

.JPG)
.JPG)