Giải bài 17 trang 80 SBT Toán 10 Cánh diều tập 1
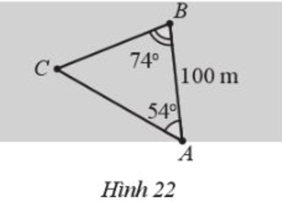
Hai người A và B cùng quan sát một con tàu đang neo đậu ngoài khơi tại vị trí C. Người A đứng trên bờ biển, người B đứng trên một hòn đảo cách bờ một khoảng AB= 100 m. Hai người tiến hành đo đạc và thu được kết quả: \(\widehat {CAB} = {54^0},\widehat {CBA} = {74^0}\) (Hình 22). Hỏi con tàu cách hòn đảo bao xa (làm tròn kết quả đến hàng phần mười theo đơn vị mét)?
Hướng dẫn giải chi tiết Bài 17
Phương pháp giải
Bước 1: Tính số đo góc \(\widehat {ACB}\)
Bước 2: Sử dụng định lí sin để tính độ dài BC của ∆ABC rồi kết luận
Lời giải chi tiết
Ta có: \(\widehat {ACB} = {180^0} - (\widehat {CBA} + \widehat {CAB}) = {52^0}\)
Áp dụng định lí sin cho ∆ABC ta có: \(\frac{{BC}}{{\sin \widehat {CAB}}} = \frac{{AB}}{{\sin \widehat {ACB}}} \Rightarrow BC = \frac{{AB.\sin \widehat {CAB}}}{{\sin \widehat {ACB}}} = \frac{{100.\sin {{54}^0}}}{{\sin {{52}^0}}} \approx 102,7\)
Vậy con tàu cách hòn đảo 102,7 m
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





