Giải bài 21 trang 81 SBT Toán 10 Cánh diều tập 1
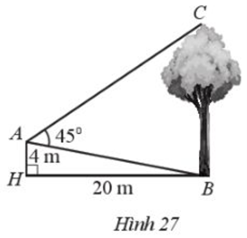
Một người đứng ở vị trí Atrên nóc một ngôi nhà cao 4 m đang quan sát đang quan sát một cây cao cách ngôi nhà 20 m và đo được \(\widehat {BAC} = {45^0}\) (Hình 27). Tính chiều cao của cây đó (làm tròn kết quả đến hàng phần mười theo đơn vị mét)
Hướng dẫn giải chi tiết Bài 21
Phương pháp giải
Bước 1: Sử dụng định lí Pytago để tính độ dài AB của ∆ABH vuông tại H
Bước 2: Sử dụng tỉ số lượng giác trong tam giác vuông để tính góc ABH rồi tính góc ABC
Bước 3: Tính góc ACB và sử dụng định lí sin để tính độ dài BC của ∆ABC rồi kết luận
Lời giải chi tiết
Áp dụng định lí Pytago cho ∆ABH vuông tại H ta có: \(AB = \sqrt {A{H^2} + H{B^2}} = \sqrt {{4^2} + {{20}^2}} \approx 20,4\) (m)
Xét ∆ABH vuông tại H có \(\tan \widehat {ABH} = \frac{{AH}}{{BH}} = \frac{1}{5} \Rightarrow \widehat {ABH} \approx 11,{3^0}\)
Ta có: \(\widehat {ABH} + \widehat {ABC} = {90^0} \Rightarrow \widehat {ABC} = {90^0} - \widehat {ABH} = 78,{7^0}\) \( \Rightarrow \widehat {ACB} = {180^0} - (\widehat {ABC} + \widehat {CAB}) = 56,{3^0}\)
Áp dụng định lí sin cho ∆ABC ta có: \(\frac{{BC}}{{\sin \widehat {BAC}}} = \frac{{AB}}{{\sin \widehat {ACB}}} \Rightarrow BC = \frac{{AB.\sin \widehat {BAC}}}{{\sin \widehat {ACB}}} = \frac{{20,4.\sin {{45}^0}}}{{\sin 56,{3^0}}} \approx 17,3\) (m)
Vậy chiều cao của cây là 17,3 m
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





