Giải bài 4.25 tr 108 SBT Toán 10
Chứng minh các bất phương trình sau vô nghiệm:
a) \({x^2} + \frac{1}{{{x^2} + 1}} < 1\)
b) \(\sqrt {{x^2} - x + 1} + \frac{1}{{\sqrt {{x^2} - x + 1} }} < 2\)
c) \(\sqrt {{x^2} + 1} + \sqrt {{x^4} - {x^2} + 1} < 2\sqrt[4]{{{x^6} + 1}}\)
Hướng dẫn giải chi tiết
a) Theo bất đẳng thức Cô – si ta có:
\(\left( {{x^2} + 1} \right) + \frac{1}{{{x^2} + 1}} \ge 2 \Rightarrow {x^2} + \frac{1}{{{x^2} + 1}} \ge 1,\forall x\)
Vì vậy bất phương trình đã cho vô nghiệm.
b) Tương tự a)
c) Tương tự a) (sử dụng bất đẳng thức)
\(\left( {a + b} \right)\left( {{a^2} - ab + {b^2}} \right) = {a^3} + {b^3}\) và đồng nhất thức \(\sqrt {\sqrt a } = \sqrt[4]{a}\).
-- Mod Toán 10 HỌC247
-


Giải BPT \(\frac{{x - 1}}{{{x^2} - 4x + 3}} < 0\)?
bởi linh thục
 22/06/2020
22/06/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Giải bất phương trình 2x - 4 > 0?
bởi Cà Thịi Lann
 21/06/2020
Tập nghiệm của bpt 2x-4>0 làTheo dõi (0) 3 Trả lời
21/06/2020
Tập nghiệm của bpt 2x-4>0 làTheo dõi (0) 3 Trả lời -


Giải hệ BPT: \(\left\{ \begin{array}{l} 4x - 5 < x + 3\\ \frac{{3x + 8}}{4} > 2x - 5 \end{array} \right.\)?
bởi Nguyễn Thị Hương Giang
 21/06/2020
21/06/2020
Giải giùm
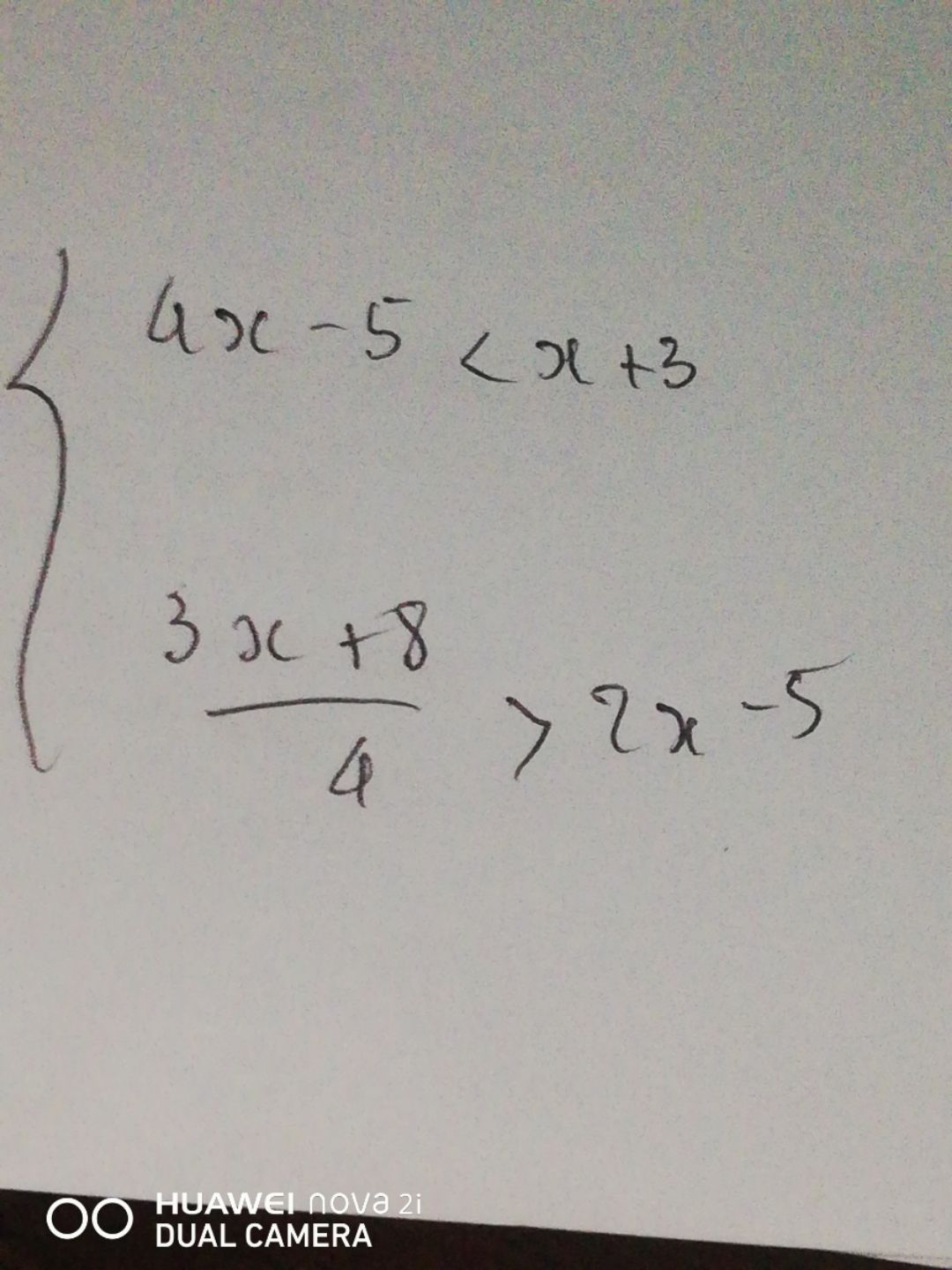 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Giải BPT \( - 1 \le \dfrac{{{x^2} - 2x + 3}}{{{x^2} + 1}} \le 2\)?
Theo dõi (0) 0 Trả lời -


Giải BPT \(\frac{{\left( {1 - x} \right)\left( { - {x^2} + x - 5} \right)}}{{1 - {x^2}}}\)?
bởi linh thục
 17/06/2020
17/06/2020
Giải giúp mình 5 bài này với ạ.Cảm ơn người giải rất nhiều ạ
 Theo dõi (1) 4 Trả lời
Theo dõi (1) 4 Trả lời -


Giải bất phương trình \(2\sqrt {x - 2} < x - 1\)?
bởi Hồ Tuyết
 14/06/2020
14/06/2020
Giải bất phương trình 2√(x-2)
Theo dõi (0) 3 Trả lời -


Số nào sau đây là nghiệm của BPT \(\frac{{\left| {1 - x} \right|}}{{\sqrt {3 - x} }} > \frac{{x - 1}}{{\sqrt {3 - x} }}\)?
bởi Len Dương
 12/06/2020
12/06/2020
Giúp em câu 7 với ạaa
 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -


 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Xác định tham số m để bất phương trình có nghiệm?
bởi Mai Pham
 11/06/2020
Cho bất phương trình... Xác định tham số m để bất phương trình có nghiệm
11/06/2020
Cho bất phương trình... Xác định tham số m để bất phương trình có nghiệm Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 4.23 trang 108 SBT Toán 10
Bài tập 4.24 trang 108 SBT Toán 10
Bài tập 4.26 trang 108 SBT Toán 10
Bài tập 4.27 trang 109 SBT Toán 10
Bài tập 4.28 trang 109 SBT Toán 10
Bài tập 4.29 trang 109 SBT Toán 10
Bài tập 4.30 trang 109 SBT Toán 10
Bài tập 4.31 trang 109 SBT Toán 10
Bài tập 4.32 trang 109 SBT Toán 10
Bài tập 4.33 trang 110 SBT Toán 10
Bài tập 21 trang 116 SGK Toán 10 NC
Bài tập 22 trang 116 SGK Toán 10 NC
Bài tập 23 trang 116 SGK Toán 10 NC
Bài tập 24 trang 116 SGK Toán 10 NC
Bài tập 25 trang 121 SGK Toán 10 NC
Bài tập 26 trang 121 SGK Toán 10 NC
Bài tập 27 trang 121 SGK Toán 10 NC
Bài tập 28 trang 121 SGK Toán 10 NC
Bài tập 29 trang 121 SGK Toán 10 NC





