Giải bài 4.32 tr 109 SBT Toán 10
Trong các khẳng định sau đây, khẳng định nào đúng?
A. \(x + 3 - \frac{1}{{x + 7}} < 2 - \frac{1}{{x + 7}} \Leftrightarrow x + 3 < 2\)
B. \(3x + 1 < x + 3 \Leftrightarrow {\left( {3x + 1} \right)^2} < {\left( {x + 3} \right)^2}\)
C. \(\sqrt {\left( {x - 1} \right)\left( {x - 2} \right)} \ge x \Leftrightarrow \sqrt {x - 1} .\sqrt {x - 2} \ge x\)
D. \(7{x^3} + 12{x^2} + 6x + 1 > 0 \Leftrightarrow 2x + 1 > x\)
Hướng dẫn giải chi tiết
Ta có : \(7{x^3} + 12{x^2} + 6x + 1 = \left( {x + 1} \right)\left( {7{x^2} + 5x + 1} \right)\)
Và \(7{x^2} + 5x + 1 = 7\left( {{x^2} + 2.\frac{5}{{14}}x + \frac{{25}}{{196}} + \frac{3}{{196}}} \right) = 7\left[ {{{\left( {x + \frac{5}{{14}}} \right)}^2} + \frac{3}{{196}}} \right] > 0,\forall x\)
Nên bpt \(7{x^3} + 12{x^2} + 6x + 1 > 0 \Leftrightarrow 2x + 1 > x\)
Đáp án D
-- Mod Toán 10 HỌC247
-


Giải bất phương trình -2x+3/5>9(2x-7)/3
bởi Phuong Anh
 05/03/2020
05/03/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Nghiệm của bất phương trình (x-1)/(2/5x+3)
bởi Cherry Chen
 02/03/2020
02/03/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm m để phương trình f(x)=(m-5)x^4-4mx^2+m-2=0 để phuorng trình có 4 nghiệm phân biệt
bởi Nguyễn Trâm Đan
 01/03/2020
01/03/2020
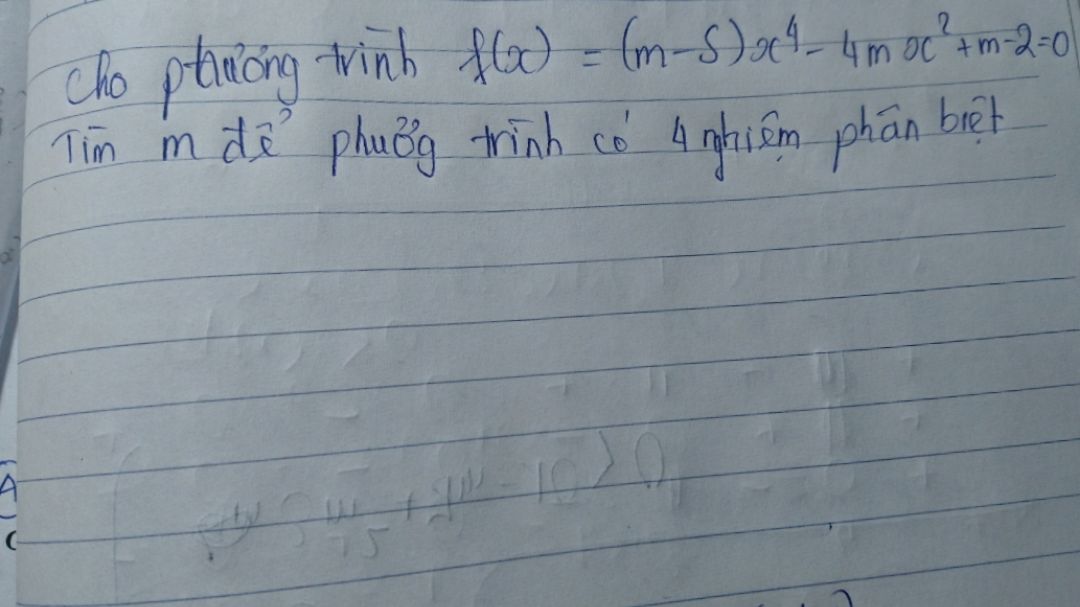 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải phương trình căn3 (x+1) +căn3 (x-1)=căn3(5x)
bởi Phạm Thủy
 28/02/2020
28/02/2020
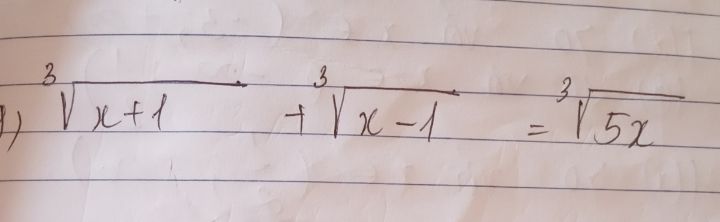 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Giải phương trình -2x+3/5 > 3(2x-7)/3
bởi Mai Xuân
 27/02/2020
27/02/2020
 Theo dõi (0) 16 Trả lời
Theo dõi (0) 16 Trả lời -

 Giải hộ mình bài 2 với
Giải hộ mình bài 2 với Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -

 .
.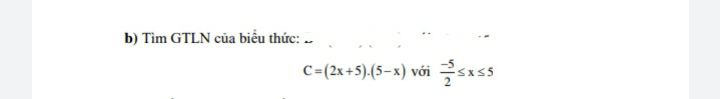 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm điều kiện của bất phương trình x cộng căn 3
bởi Chibi Kiên
 24/02/2020
Tìm điều kiện của bất phương trình x cộng căn 3Theo dõi (0) 0 Trả lời
24/02/2020
Tìm điều kiện của bất phương trình x cộng căn 3Theo dõi (0) 0 Trả lời -


 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 4.30 trang 109 SBT Toán 10
Bài tập 4.31 trang 109 SBT Toán 10
Bài tập 4.33 trang 110 SBT Toán 10
Bài tập 21 trang 116 SGK Toán 10 NC
Bài tập 22 trang 116 SGK Toán 10 NC
Bài tập 23 trang 116 SGK Toán 10 NC
Bài tập 24 trang 116 SGK Toán 10 NC
Bài tập 25 trang 121 SGK Toán 10 NC
Bài tập 26 trang 121 SGK Toán 10 NC
Bài tập 27 trang 121 SGK Toán 10 NC
Bài tập 28 trang 121 SGK Toán 10 NC
Bài tập 29 trang 121 SGK Toán 10 NC






