Giải bài 2.7 tr 82 SBT Hình học 10
Cho \(\cos \alpha = \frac{{ - \sqrt 2 }}{4}\). Tính sin α và tan α
Hướng dẫn giải chi tiết
Vì \(\cos \alpha < 0\) nên \({90^0} < \alpha < {180^0} \Rightarrow \sin \alpha > 0\)
\(\begin{array}{l}
in\alpha = \sqrt {1 - {{\cos }^2}\alpha } = \sqrt {1 - {{\left( {\frac{{\sqrt 2 }}{4}} \right)}^2}} = \frac{{\sqrt {14} }}{4}\\
\Rightarrow \tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = - \sqrt 7
\end{array}\)
-- Mod Toán 10 HỌC247
-


Tìm các giá trị lượng giác của các góc \({150^0}\)
bởi A La
 19/02/2021
Theo dõi (0) 1 Trả lời
19/02/2021
Theo dõi (0) 1 Trả lời -


Tìm các giá trị lượng giác của các góc \({120^0}\)
bởi bach dang
 20/02/2021
Theo dõi (0) 1 Trả lời
20/02/2021
Theo dõi (0) 1 Trả lời -

 A . 30° B . 45° C. 60° D. 90°Theo dõi (0) 2 Trả lời
A . 30° B . 45° C. 60° D. 90°Theo dõi (0) 2 Trả lời -

 Câu 23 ạ
Câu 23 ạ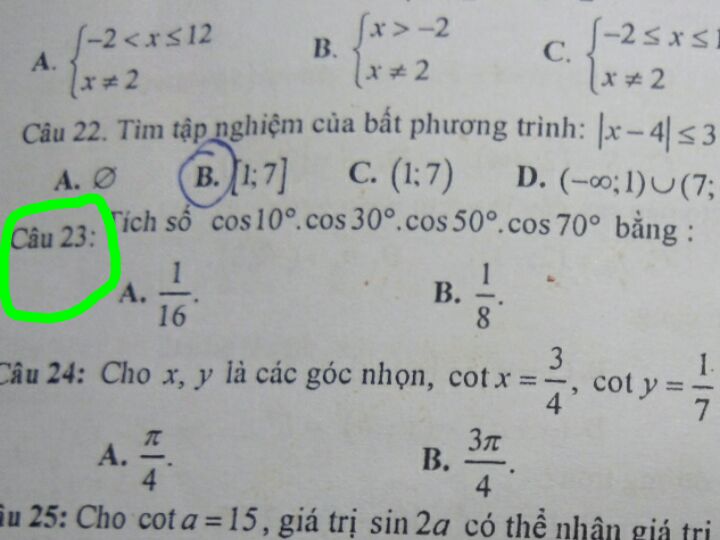 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời
Bài tập SGK khác
Bài tập 2.5 trang 82 SBT Hình học 10
Bài tập 2.6 trang 82 SBT Hình học 10
Bài tập 2.8 trang 82 SBT Hình học 10
Bài tập 2.9 trang 82 SBT Hình học 10
Bài tập 2.10 trang 82 SBT Hình học 10
Bài tập 2.11 trang 82 SBT Hình học 10
Bài tập 2.12 trang 82 SBT Hình học 10
Bài tập 1 trang 43 SGK Hình học 10 NC






