Giải bài 1.27 tr 14 SBT Đại số 10
Cho hai tập hợp A, B biết A ⊂ B. Tìm mệnh đề đúng trong các mệnh đề sau:
A. A∪B = A
B. A∩B = B
C. A∖B = ∅
D. B∖A = A
Hướng dẫn giải chi tiết
A ⊂ B ⇔ ∀x(x ∈ A ⇒ x ∈ B)
Đáp án A sai vì A ∪ B = A ⇔ {x|x ∈ A hoặc x ∈ B} = {x|x ∈ A}. Suy ra B ⊂ A (không thỏa mãn đề bài)
Đáp án B sai vì A∩B = B ⇔ {x|x ∈ A và x ∈ B} = {x|x ∈ B}. Suy ra B ⊂ A (không thỏa mãn đề bài)
Đáp án C đúng vì A∖B = ∅ ⇔ {x|x ∈ A và x ∉ B} = ∅. Suy ra nếu x ∈ A thì x ∈ B. Vậy A ⊂ B (thỏa mãn đề bài)
Đáp án D sai vì B∖A = A ⇔ {x|x ∈ B và x ∉ A} = {x|x ∈ A} (vô lý)
Đáp án đúng: C
-- Mod Toán 10 HỌC247
-

 Cho A=(-2;10) và B=(m:m 2) Tìm m để A giao B khác tập rỗngTheo dõi (1) 3 Trả lời
Cho A=(-2;10) và B=(m:m 2) Tìm m để A giao B khác tập rỗngTheo dõi (1) 3 Trả lời -


Xác định A hợp B biết A=(-vô cực;1) hợp [1;+ vô cực)
bởi Linh Le
 23/11/2019
23/11/2019
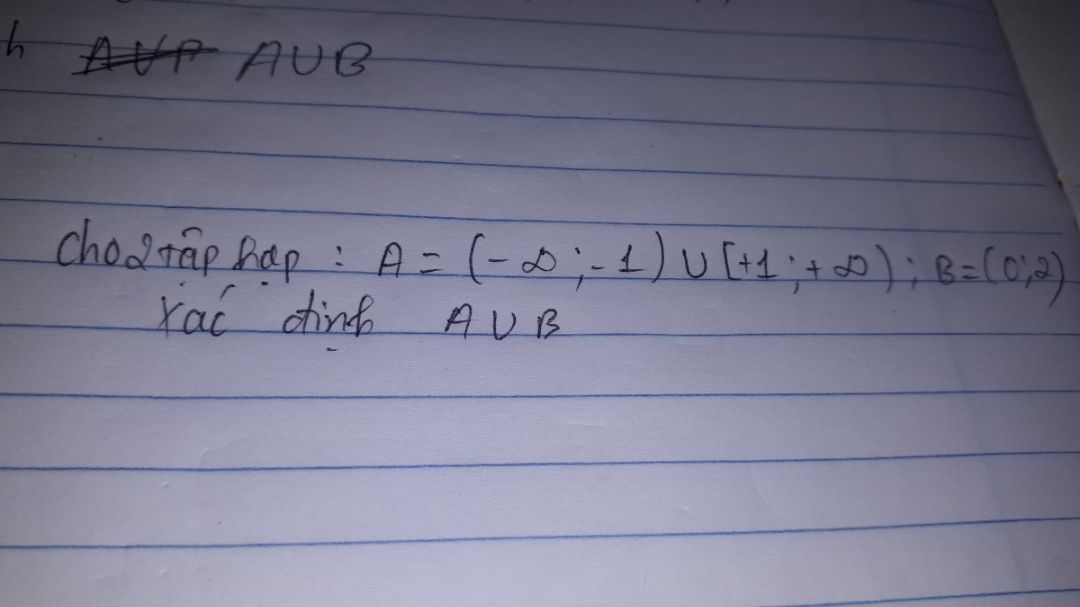 Theo dõi (2) 2 Trả lời
Theo dõi (2) 2 Trả lời -

 Giải cho với
Giải cho với Theo dõi (1) 5 Trả lời
Theo dõi (1) 5 Trả lời -


Tìm m để hàm số y=|f(x)| đồng biến trên khoảng (-1;1)
bởi Thuỳ Trang
 22/10/2019
22/10/2019
cho hs y= f(x) = x^2 -2(m+1)x+1 -m
có bnhiu giá trị nguyên của tham số m để hs y = | f(x) | đb trên khoảng (-1,1)Theo dõi (1) 0 Trả lời -


Cho tập hợp X ={1,2,3,4} câu nào sau đây đúng ?
bởi Trần Linh
 01/10/2019
Cho tập hợp X ={1,2,3,4} . Câu nào sau đây đúng ? A) số tập con của X là 16B) số tập con của X gồm có 2 phần tử là 8C) số tập con của X chứa số 1 là 6D) số tập con của X gồm vó 3 phần tử là 2Theo dõi (0) 2 Trả lời
01/10/2019
Cho tập hợp X ={1,2,3,4} . Câu nào sau đây đúng ? A) số tập con của X là 16B) số tập con của X gồm có 2 phần tử là 8C) số tập con của X chứa số 1 là 6D) số tập con của X gồm vó 3 phần tử là 2Theo dõi (0) 2 Trả lời -


Trong một nhóm học sinh có 100 học sinh, có 29 học sinh giỏi toán, 30 học sinh giỏi anh, 42 học sinh giỏi văn. Trong có có 8 người vừa giỏi văn vừa giỏi anh, 10 người vừa giỏi toán vừa giỏi văn, 5 người vừa giỏi anh vừa giỏi văn, 3 người giỏi cả 3 môn. Hỏi có bao nhiêu người chỉ giỏi toán
Theo dõi (0) 16 Trả lời -


Tính và biểu diễn trên trục số (-∞;3) ∪ (2; +∞))
bởi Trần Uyên
 16/10/2018
16/10/2018
Tính và biểu diễn trên trục số các tập hợp sau:
a) (-∞;3) ∪ (2; +∞))
b) R\((0;5) ∩ (3;4)
Theo dõi (0) 2 Trả lời -


Có tất cả bao nhiêu giá trị nguyên m để A giao B khác 0 biết A=[m;m+2] ?
bởi Phan Trung Hiếu
 10/10/2018
10/10/2018
Chiều hôm nay mình mới làm bài kiểm tra 1 tiết Toán xong, và cả lớp mình chỉ cãi nhau về bài toán này, nên mình muốn up lên đây để mong các bạn hoặc các thầy cô giải đáp bài toán này.
Câu hỏi: Cho hai tập
và
. Có tất cả bao nhiêu giá trị nguyên m để A giao B khác 0 ?
A: Vô số
B: 3
C: 5
D: 1
Theo dõi (1) 3 Trả lời -


Chứng minh nếu A ∆ B =A thì B rỗng
bởi Trịnh Lan Trinh
 13/10/2018
13/10/2018
Cho 2 tập hợp A và B . Hiệu đỗi ứng của A và B biết kí hiệu là A ∆ B, là tập hợp các phần tử thuộc A hoặc thuộc B nhưng ko thuộc cả A và B
a) c/m nếu A ∆ B =A thì B rỗng
b) c/m nếu A ∆ C=B ∆ C thì A=BTheo dõi (0) 1 Trả lời -


Tìm tập hợp A giao B biết A=[1;7] ;B= Z
bởi thu phương
 13/10/2018
13/10/2018
A=[1;7] ;B= Z tim A giao B ; A hop B
Theo dõi (0) 1 Trả lời -


Tìm tập hợp A giao B biết A=(-1;+ vô cực) và B=(1;2)
bởi Hương Lan
 13/10/2018
13/10/2018
tìm \(A\cap B\) ; \(A\cup B\) trong trường hợp sau:
\(A=(-1;+\infty)\) và B = (1;2)
Theo dõi (0) 1 Trả lời






