-
Câu hỏi:
Cho đồ thị \(\left( C \right):y=\frac{x}{x-1}\). Đường thẳng \(d\) đi qua điểm \(I\left( 1;1 \right)\) cắt \(\left( C \right)\) tại hai điểm phân biệt \(A\) và \(B\). Khi diện tích tam giác \(MAB\) đạt giá trị nhỏ nhất, với \(M\left( 0;3 \right)\) thì độ dài đoạn \(AB\) bằng
- A. \(\sqrt{10}\).
- B. \(\sqrt{6}\).
- C. \(2\sqrt{2}\).
- D. \(2\sqrt{3}\).
Lời giải tham khảo:
Đáp án đúng: A
Chọn A
Gọi \(A\left( 1-m;\frac{1-m}{-m} \right);B\left( 1+m;\frac{m+1}{m} \right)\) với \(m>0\).
\(I\left( 1;1 \right)\) là tâm đối xứng của đồ thị hàm số, suy ra \(I\) là trung điểm của \(A,B\).
\({{S}_{\Delta MAB}}=2{{S}_{\Delta MIB}}\) nên \({{S}_{\Delta MAB}}\min \) khi \({{S}_{\Delta MIB}}\) min.
Phương trình đường thẳng \(MI:2x+y-3=0\).
Ta có
\({{S}_{MIB}}=\frac{1}{2}ah=\frac{1}{2}d\left( B;IM \right).IM=\frac{1}{2}\left| \frac{2{{m}^{2}}-m+1}{m} \right|\)
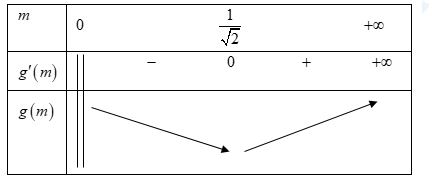
Xét hàm số \(g\left( m \right)=\frac{2{{m}^{2}}-m+1}{m}\)
\({g}'\left( m \right)=\frac{2{{m}^{2}}-1}{{{m}^{2}}}\)
Ta có bảng biến thiên
Suy ra \(\underset{m>0}{\mathop{\min \left| g\left( m \right) \right|}}\,=2\sqrt{2}-1\) khi \(m=\frac{1}{\sqrt{2}}\).
Khi đó \(IB=\sqrt{{{m}^{2}}+\frac{1}{{{m}^{2}}}}=\sqrt{\frac{5}{2}}\) suy ra \(AB=2IB=\sqrt{10}\).
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Cho hình lập phương \(ABCD.{A}'{B}'{C}'{D}'\). Góc giữa hai đường thẳng \(AB\) và \({B}'{D}'\) bằng
- Biết \(\int\limits_{0}^{1}{f\left( x \right)}dx=\frac{1}{3}\) và
- Tập xác định của hàm số \(y=\log x+\log \left( 3-x \right)\) là
- Cho hàm số \(y=f\left( x \right)\) có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào
- Cho góc ở đỉnh của một hình nón bằng \({{60}^{0}}\). Gọi \(r,h,l\) lần lượt là
- Trong không gian \(Oxyz\), đường thẳng \(\Delta \) đi qua \(A\left( -1;-1;1 \right)\)
- Cho các số phức \(z=2+i\) và \(w=3-i.\) Phần thực của số phức \(z+w\) bằng:
- Họ các nguyên hàm của hàm số \(f(x)=\sin 3x\) là
- Cho cấp số cộng \(\left( {{u}_{n}} \right)\) có \({{u}_{1}}=1\) và \({{u}_{3}}=\frac{1}{3}\). Công sai của \(\left( {{u}_{n}} \right)\) bằng
- Cho hàm số \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng xét dấu đạo hàm
- Chu vi đường tròn lớn của mặt cầu \(S\left( O;R \right)\) là
- Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như hình bên. Giá trị lớn nhất của hàm số đã cho trên đoạn \(\left[ -3;3 \right]\) bằng
- Trong không gian \(Oxyz\), một véctơ pháp tuyến của mặt phẳng \(\left( Oyz \right)\) là
- Nghiệm của phương trình \({{2}^{x-1}}=8\) là
- Cho hàm số \(y=f\left( x \right)\) có đồ thị như hình bên. Hỏi phương trình \(2f\left( x \right)=5\) có bao nhiêu nghiệm trên đoạn \(\left[ -1;2 \right]\)?
- Gọi \({{z}_{1}}\), \({{z}_{2}}\) là các nghiệm phức của phương trình \({{z}^{2}}-3z+5=0\). Môđun của số phức \(\left( 2{{{\bar{z}}}_{1}}-3 \right)\left( 2{{{\bar{z}}}_{2}}-3 \right)\) bằng
- Đồ thị hàm số \(y=\frac{x+3}{{{x}^{3}}-3x}\) có bao nhiêu đường tiêm cận?
- Cho hàm số bậc ba \(y=f\left( x \right)\)có đồ thị như hình vẽ. Phương trình \(f\left( {{x}^{2}} \right)+1=0\) có bao nhiêu nghiệm?
- Một khối trụ có đường cao bằng \(2\), chu vi của thiết diện qua trục gấp \(3\)lần đường kính đáy. Thể tích của khối trụ đó bằng
- Đạo hàm của hàm số \(f\left( x \right)=\frac{{{2}^{x}}-1}{{{2}^{x}}+1}\) là
- Giả sử \(f\left( x \right)\) là hàm liên tục \(\left( 0;\,+\infty \right)\) và diện tích hình phẳng được kẻ sọc hình bên bằng \(3\).
- Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(a\), \(O\) là tâm mặt đáy. Khoảng cách giữa hai đường thẳng \(SO\) và \(CD\) bằng
- Trong không gian \(Oxyz\), đường thẳng \(\Delta :\frac{x}{1}=\frac{y-1}{1}=\frac{z}{-1}\) song song với mặt phẳng nào sau đây?
- Họ các nguyên hàm của hàm số \(f\left( x \right)={{3}^{2x-1}}\) là
- Cho các số thực dương \(a\,,\,b\)thỏa mãn \({{\log }_{2}}\left( a+b \right)=3+{{\log }_{2}}ab\). Giá trị \(\frac{1}{a}+\frac{1}{b}\)bằng
- Cho khối lăng trụ tam giác \(ABC.{A}'{B}'{C}'\)có cạnh \(A{A}'=2a\) và tạo với mặt phẳng đáy một góc bằng \(60{}^\circ \),
- Trong không gian \(Oxyz,\) cho đường thẳng \(\Delta \) là giao tuyến của hai mặt phẳng \(\left( \alpha \right):x+y+z+1=0\)
- Hàm số \(f\left( x \right)={{x}^{4}}{{\left( x-1 \right)}^{2}}\) có bao nhiêu điểm cực trị?
- Một tổ học sinh có 12 bạn, gồm 7 nam và 5 nữ. Cần chọn một nhóm 3 học sinh của tổ đó để làm vệ sinh lớp học.
- Có bao nhiêu số nguyên \(m\)để hàm số \(f\left( x \right)=3x+m\sqrt{{{x}^{2}}+1}\) đồng biến trên \(\mathbb{R}\)?
- Giả sử hàm số \(f\left( x \right)\) có đạo hàm liên tục trên. Biết rằng \(G\left( x \right)={{x}^{3}}\) là một nguyên hàm của \(g\left( x \right)={{e}^{-2x}}f\left( x \right)\) trên \(\mathbb{R}\).
- Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Mặt bên \(SAB\) là tam giác đều cạnh \(\sqrt{3}a\), \(ABC\) là tam giác vuông tại \(A\) có cạnh \(AC=a\),
- Cho hàm số \(y=a{{x}^{3}}+b{{x}^{2}}+cx+d\) (với \(a,b,c,d\in \mathbb{R}\)) có đồ thị như hình vẽ
- Có bao nhiêu số phức \(z\)đôi một khác nhau thỏa mãn \(\left| z+i \right|=2\) và \({{\left( z-2 \right)}^{4}}\) là số thực?
- Có \(10\) học sinh gồm \(5\) bạn lớp \(12A\) và \(5\) bạn lớp \(12B\) tham gia một trò chơi. Để thực hiện trò chơi, người điều khiển ghép ngẫu nhiên \(10\) học sinh đó thành \(5\) cặp
- Một chiếc xe đua \({{F}_{1}}\) đạt tới vận tốc lớn nhất là \(360\,km/h\). Đồ thị bên biểu thị vận tốc \(v\) của xe trong \(5\) giây đầu tiên kể từ lúc xuất phát.
- Trong không gian \(Oxyz\), cho mặt phẳng \(\left( \alpha \right)\) vuông góc với \(\Delta :\frac{x}{1}=\frac{y}{-2}=\frac{z}{3}\) và
- Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân, \(AB=BC=2a\).
- Cho đồ thị \(\left( C \right):y=\frac{x}{x-1}\). Đường thẳng \(d\) đi qua điểm \(I\left( 1;1 \right)\) cắt \(\left( C \right)\) tại hai điểm phân biệt \(A\) và \(B\).
- Cho hình lăng trụ đứng \(ABC.{A}'{B}'{C}'\) có \(AB=A{A}'=2a\), \(AC=a\), \(\widehat{BAC}=120{}^\circ \). Bán kính mặt cầu ngoại tiếp hình chóp \(A.BC{C}'{B}'\) bằng
- Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right):ax+by+cz+7=0\)
- Cho hàm số \(f\left( x \right)\) nhận giá trị dương và có đạo hàm liên tục trên \(\left[ 1;\ e \right]\). Biết \(f\left( 1 \right)=1\)
- Biết khoảng (a;b) là tập hợp tất cả các giá trị dương của tham số m để phương trình
- Xét các số phức \(z=a+bi,\,\,\left( a,\,\,b\in \mathbb{R} \right)\) thỏa mãn \(\left| z-2+3i \right|=4\) và \(\left| z+1-4i \right|+\left| z-9 \right|\) đạt giá trị lớn nhất.
- Cho hàm số \(f\left( x \right)\) là hàm số đa thức bậc bốn. Biết \(f\left( 0 \right)=0\) và đồ thị hàm số \(y={f}'\left( x \right)\) có hình vẽ bên dưới.
- Cho khối chóp S.ABCD có đáy là ABCD
- Giả sử \(f\left( x \right)\) là hàm có đạo hàm liên tục trên khoảng \(\left( 0;\pi \right)\)
- Có bao nhiêu số nguyên \(a\) để phương trình \({{z}^{2}}-\left( a-3 \right)z+{{a}^{2}}+a=0\)
- Xét tất cả các số thực dương \(x;y\) thỏa mãn \(\frac{x+y}{10}+\log \left( \frac{1}{2x}+\frac{1}{2y} \right)=1+2xy\). Khi biểu thức \(\frac{4}{{{x}^{2}}}+\frac{1}{{{y}^{2}}}\) đạt giá trị nhỏ nhất
- Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right):{{x}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z+3 \right)}^{2}}=24\) cắt mặt phẳng \(\left( \alpha \right):x+y=0\) theo giao tuyến là đường tròn