Phương pháp tìm hình chiếu của các khối đa diện

Các khối là các vật thể trong không gian với kích thước bao gồm chiều dài, chiều rộng và chiều cao nhưng khi cần mô tả hình dạng của một khối, ta chỉ có thể biểu diễn trên giấy, hay nói cách khác là trên một mặt phẳng. Những hình ảnh biểu diễn đó thực chất chỉ là các hình chiếu song song của vật thể lên giấy.

Hình chiếu song song của một vật lên một mặt phẳng là gì? Trước hết ta nhắc lại định nghĩa của phép chiếu song song trong không gian.

Hình 3.4.1.a

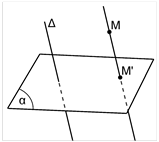
Cho một mặt phẳng \(\left( \alpha  \right)\) và một đường thẳng \(\left( \Delta  \right)\) cắt \(\left( \alpha  \right)\). Qua điểm M bất kỳ, ta vẽ đường thẳng d song song hoặc trùng với \(\left( \Delta  \right)\) và cắt \(\left( \alpha  \right)\) tại M’.

Khi đó M’ gọi là hình chiếu của M lên mặt phẳng \(\left( \alpha  \right)\) theo phương \(\left( \Delta  \right)\). Mặt phẳng \(\left( \alpha  \right)\) gọi là mặt phẳng chiếu, phương của \(\left( \Delta  \right)\) gọi là phương chiếu. (xem hình 3.4.1.a)

Tương tự, hình chiếu của hình (H) lên mặt phẳng \(\left( \alpha  \right)\) theo phương \(\left( \Delta  \right)\) là tập hợp các hình chiếu của các điểm thuộc hình (H) lên mặt phẳng \(\left( \alpha  \right)\) theo phương \(\left( \Delta  \right)\). (xem hình 3.4.1.b)

Hình 3.4.1.b

Khi đường thẳng \(\left( \Delta  \right)\) vuông góc với mặt phẳng \(\left( \alpha  \right)\), ta có phép chiếu vuông góc. Hình chiếu tạo ra từ phép chiếu vuông góc gọi là hình chiếu vuông góc (hay còn gọi tắt là hình chiếu).

Như đã nói, các hình biểu diễn của các vật thể trong không gian lên giấy thực chất là các hình chiếu song song của vật thể theo một phương chiếu nào đó. Trong thực tế, ta rất hay sử dụng phép chiếu vuông góc để vẽ các hình biểu diễn của vật như trong các bản vẽ kỹ thuật chẳng hạn. Trong hình 3.4.2.a, ta có một thiết bị máy (hình ở góc dưới bên trái) được quan sát trực diện và quan sát từ một bên. Hai hướng nhìn khác nhau tương ứng với 2 phương chiếu khác nhau, từ đó ta có 2 hình chiếu như trong bản vẽ (hình 3.4.2.b và 3.4.2.c)

                      

                  Hình 3.4.2.a                          Hình 3.4.2.b                Hình 3.4.2.c

Bài 1: Vẽ hình chiếu vuông góc của khối lập phương với phương chiếu là phương của một cạnh khối này.

· Khi phương chiếu là phương của một cạnh, đồng nghĩa với việc phương chiếu sẽ vuông góc với một mặt của khối lập phương. Hình chiếu được yêu cầu vẽ là hình chiếu vuông góc, do đó mặt phẳng chiếu cũng song song với mặt của khối lập phương vừa nêu.

· Hình chiếu ta thu được sẽ là hình vuông và là một mặt của khối lập phương.

Hướng dẫn giải

Hình 3.5.1.a         

Hình 3.5.1.b: Hình chiếu của khối lập phương

Dựa vào mô tả về phương chiếu của đề bài để xác định hình chiếu, thông thường phương chiếu sẽ là phương vuông góc với một mặt nào đó của vật.

Bài 2: Vẽ hình chiếu của khối chóp tứ giác đều với phương chiếu trùng với phương của một cạnh đáy.

· Mặt phẳng chiếu sẽ là mặt phẳng vuông góc với cạnh đáy được chọn.

· Dựng đường cao của khối chóp, qua đó dựng mặt phẳng vuông góc với phương chiếu. Thiết diện của khối chóp khi bị cắt bởi mặt phẳng này cũng chính là hình chiếu ta cần vẽ.

Hướng dẫn giải

Hình chiếu của khối chóp tứ giác đều là một tam giác cân tại đỉnh của khối chóp.

Hình 3.5.2.a                             

Hình 3.5.2.b: Hình chiếu của khối chóp

Bài tập tương tự

Bài 3: Vẽ hình chiếu của khối chóp tứ giác đều với phương chiếu trùng với phương của đường cao.

Bài 4: Vẽ hình chiếu của khối tứ diện đều với phương chiếu trùng với phương của đường cao.

Bài 5: Vẽ hình chiếu của một khối hộp đứng có đáy là hình thoi với phương chiếu trùng với phương của một đường chéo của đáy.

Bài 6: Cho một ngôi nhà có dạng hình lăng trụ ngũ giác đứng như hình vẽ. Vẽ hình chiếu của ngôi nhà với phương chiếu:

Hình 3.5.3.a

a. Vuông góc với mặt có cửa ra vào.

b. Vuông góc với mặt có cửa sổ.

c. Vuông góc với sàn nhà.

·Nắm rõ được cấu trúc của ngôi nhà, ta có thể xác định được hình chiếu trong từng trường hợp.

Hình 3.5.3.b

Hướng dẫn giải

Hình 3.5.3.c: câu a   

Hình 3.5.3.d: câu b     

Hình 3.5.3.e: câu c

Bài tập tương tự

Bài 7: Vẽ hình chiếu của một chiếc lọ có dạng hình trụ với phương chiếu vuông góc với đường cao.

Bài 8: Vẽ hình chiếu của một chiếc nón có dạng hình nón khi phương chiếu trùng với phương của đường cao.

Bài 9: Vẽ hình chiếu của một chiếc cốc có dạng hình nón cụt (đáy nhỏ nằm trên đáy dưới) khi phương chiếu trùng với phương của đường cao.

                          ​

Hình 3.5.4                                 Hình 3.5.5                                 Hình 3.5.6

Bài 10: Một mẩu ghép hình có dạng hình lập phương và các nút dạng trụ nằm trên một mặt của khối (xem hình 3.5.7). Hãy vẽ hình chiếu của mẩu ghép hình này khi phương chiếu vuông góc với một mặt của nó.

 

...

--(Nội dung đầy đủ, chi tiết vui lòng xem tại online hoặc đăng nhập để tải về máy)---

Trên đây là một phần trích đoạn nội dung Phương pháp tìm hình chiếu của các khối đa diện. Để xem thêm nhiều tài liệu tham khảo hữu ích khác các em chọn chức năng xem online hoặc đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.

Hy vọng tài liệu này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong học tập.

Các em quan tâm có thể tham khảo thêm các tài liệu cùng chuyên mục:

• Một số bài toán về mô hình các khối đa diện

• Phương pháp phân chia và lắp ráp khối đa diện

Chúc các em học tập tốt!