Đề cương ôn tập HK1 môn Toán 12 năm học 2022-2023

- Xét tính đồng biến, nghịch biến của hàm số trên một khoảng.

- Quy tắc xét tính đơn điệu của hàm số

• Tìm tập xác định
• Tính đạo hàm f'(x). Tìm các điểm x_i (i= 1 , 2 ,..., n) mà tại đó đạo hàm bằng 0  hoặc không xác định.
• Sắp xếp các điểm x_i theo thứ tự tăng dần và lập bảng biến thiên.
• Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.

- Quy tắc tìm cực trị của hàm số

+ Bước 1: Tìm tập xác định của hàm số.

+ Bước 2: Tính (f'(x), tìm các điểm tại đó (f'(x) = 0 hoặc không xác định.

+  Bước 3: Lập bảng biến thiên và kết luận.

• Tại các điểm mà đạo hàm đổi dấu từ âm sang dương thì đó là điểm cực tiểu của hàm số.
• Tại các điểm mà đạo hàm đổi dấu từ dương sang âm thì đó là điểm cực đại của hàm số.

- Quy tắc tìm GTLN, GTNN của hàm số y = f(x) liên tục trên đoạn [a ; b]

+ Tìm các điểm x_i ∈ (a ; b)(i = 1, 2, . . . , n) mà tại đó f'(x_i) = 0 hoặc f'(x_i) không xác định.

+ Tính f(a), f(b), f(x_i) (i = 1, 2, . . . , n) .

+ Khi đó: \(\underset{[a;b]}{\mathop{\max }}\,f(x)=\max \left\{ f(a);f(b);f({{x}_{i}}) \right\}\); \(\underset{[a;b]}{\mathop{\min }}\,f(x)=\min \left\{ f(a);f(b);f({{x}_{i}}) \right\}\)

- Tiệm cận đứng: Đường thẳng x=a là đường tiệm cận đứng của (C) nếu ít nhất một trong bốn điều kiện sau được thoả mãn:

\(\begin{array}{l}
\mathop {\lim }\limits_{x \to {a^ + }} {\mkern 1mu} f(x) =  + \infty \\
\mathop {\lim }\limits_{x \to {a^ + }} {\mkern 1mu} f(x) =  - \infty \\
\mathop {\lim }\limits_{x \to {a^ - }} {\mkern 1mu} f(x) =  + \infty \\
\mathop {\lim }\limits_{x \to {a^ - }} {\mkern 1mu} f(x) =  - \infty 
\end{array}\)

- Tìm điều kiện của tham số để đồ thị hàm số phân thức có tiệm cận đứng.

• Bước 1: Tìm điều kiện để mẫu thức có nghiệm (nếu cần) và tính các nghiệm {x₁},{x₂},...,{x_n} của mẫu thức.
• Bước 2: Nêu điều kiện để hàm phân thức có tiệm cận đứng:
• Hàm số có một (hai, ba,…) tiệm cận đứng nếu mẫu thức có một (hai, ba,…) nghiệm không là nghiệm của tử thức.
• Bước 3: Thay các nghiệm {x₁},{x₂},...,{x_n} lên tử thức và biện luận dựa trên yêu cầu đề bài về số tiệm cận đứng.

- Tiệm cận ngang: Đường thẳng y = b là tiệm cận ngang của (C) nếu ít nhất một trong các điều kiện sau được thỏa mãn:

\(\begin{array}{l}
\mathop {\lim }\limits_{x \to  + \infty } {\mkern 1mu} f(x) = b\\
\mathop {\lim }\limits_{x \to  - \infty } {\mkern 1mu} f(x) = b
\end{array}\) 

- Các bước khảo sát và vẽ đồ thị hàm số y = f(x)

i) Tìm tập xác định của hàm số.

ii) Sự biến thiên 

+ Xét sự biến thiên của hàm số

• Tìm đạo hàm bậc nhất y';
• Tìm các điểm tại đó y' bằng 0 hoặc không xác định ;
• Xét dấu y' và suy ra chiều biến thiên của hàm số.

+ Tìm cực trị.

+ Tìm các giới hạn tại vô cực, các giới hạn vô cực và tìm các tiệm cận (nếu có).

+ Lập bảng biến thiên tổng kết các bước trên để hình dung ra dáng điệu của đồ thị

iii) Vẽ đồ thị (thể hiện các cực trị, tiệm cận, giao của đồ thị với các trục, . . .)

- Tương giao của các đồ thị

Cho hai đồ thị (C₁): y = f(x); và (C₂): y = g(x).

Phương trình xác định hoành độ giao điểm của \((C_{1})\) và (C₂) là: f(x)=g(x). (1)

+ Nếu (1) vô nghiệm thì (C₁) và (C₂) không có điểm chung (không cắt nhau và không tiếp xúc với nhau).

+ Nếu (1) có n nghiệm phân biệt thì (C₁) và (C₂) giao nhau tại n điểm phân biệt. Nghiệm của (1) chính là hoành độ các giao điểm.

- Viết phương trình tiếp tuyến của đồ thị

+ Viết phương trình tiếp tuyến của đồ thị hàm số tại một điểm.

• Bước 1: Tính \({y}'={f}'\left( x \right)\Rightarrow {f}'\left( {{x}_{0}} \right)\)
• Bước 2: Viết phương trình tiếp tuyến \(y={f}'\left( {{x}_{0}} \right)\left( x-{{x}_{0}} \right)+f\left( {{x}_{0}} \right)\)
• Bước 3: Kết luận.

+ Viết phương trình tiếp tuyến của đồ thị hàm số đi qua một điểm.

• Bước 1: Tính \({y}'={f}'\left( x \right)\)
• Bước 2: Viết phương trình tiếp tuyến tại điểm có hoành độ x₀ của \(\left( C \right):\text{ }y={f}'\left( {{x}_{0}} \right)\left( x-{{x}_{0}} \right)+f\left( {{x}_{0}} \right)\)
• Bước 3: Thay tọa độ \(\left( {{x_M};{y_M}} \right)\) vào phương trình trên, giải phương trình tìm \({x_0}\).
• Bước 4: Thay mỗi giá trị \({x_0}\) tìm được vào phương trình tiếp tuyến ta được phương trình cần tìm.

- Lũy thừa và logarit

Cho n là một số nguyên dương. Với a là một số thực tùy ý, lũy thừa bậc n của a là tích của n thừa số a.

\({{a}^{n}}=a.a.a.....a\) (n thừa số a). Với \(a\ne 0\) thì \({{a}^{0}}=1,{{a}^{-n}}=\frac{1}{{{a}^{n}}}\)

- Hàm số mũ và hàm số lôgarit

+ Hàm số \(y={{x}^{\alpha }}\) có đạo hàm tai mọi x ∈ (0; +∞) và \({y}'={{\left( {{x}^{\alpha }} \right)}^{\prime }}=\alpha {{x}^{\alpha -1}}\) 

+ Nếu hàm số u=u(x) nhận giá trị dương và có đạo hàm trong khoảng J thì hàm số \(y={{u}^{\alpha }}\left( x \right)\) cũng có đạo hàm trên J và \({y}'={{\left[ {{u}^{\alpha }}\left( x \right) \right]}^{\prime }}=\alpha {{u}^{\alpha -1}}\left( x \right){u}'\left( x \right)\) 

- Phương trình mũ cơ bản có dạng \({a^x} = b\left( {0 < a \ne 1} \right)\) 

+) Với b > 0 ta có \({{a}^{x}}=b\Leftrightarrow x={{\log }_{a}}b\)

+) Với \(b\le 0\) phương trình vô nghiệm.

- Phương trình lôgarit dạng  \({\log _a}x = b{\rm{ }}\left( {0 < a \ne 1} \right)\) 

Ta có: \({{\log }_{a}}x=b\Leftrightarrow x={{a}^{b}}\)

Phương trình luôn có nghiệm \(x={{a}^{b}}\)

- Tính thể tích khối lăng trụ và khối chóp.

+ Nếu khối chóp đã cho có chiều cao h và diện tích đáy B thì thể tích tính theo công thức \(V=\frac{1}{3}Bh\) 

+ Thể tích khối lăng trụ

V = B.h với B là diện tích đáy, h là chiều cao

+ Thể tích khối hộp chữ nhật

V = abc với a, b, c là ba kích thước

+Thể tích khối lập phương

\(V={{a}^{3}}\) với a là độ dài cạnh

- Tính tỉ số thể tích.

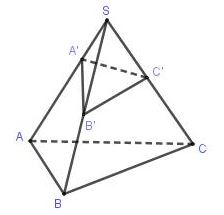
+) Cho khối chóp \(S.ABC,{A}'\in SA,{B}'\in SB,{C}'\in SC\). Khi đó \(\frac{{{V}_{S.{A}'{B}'{C}'}}}{{{V}_{S.ABC}}}=\frac{S{A}'}{SA}.\frac{S{B}'}{SB}.\frac{S{C}'}{SC}\) 

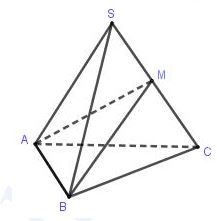
+) Với điểm \(M\in SC\) ta có: \(\frac{{{V}_{S.ABM}}}{{{V}_{S.ABC}}}=\frac{SM}{SC}\) 

Câu 1. Hình đa diện đều có tất cả các mặt là ngũ giác có bao nhiêu cạnh?

A. 60 .                                

B. 20 .                                

C. 12 .                                

D. 30 .

Câu 2. Khối trụ tròn xoay có diện tích đáy là B, đường cao h, thể tích khối trụ là:

A. \(V=\pi {{B}^{2}}h\).    

B. \(V=2Bh\).                     

C. \(V=Bh\).                      

D. \(V=\frac{1}{3}Bh\).

Câu 3. Tập xác định của hàm số \(y={{(x-2)}^{-4}}+\text{lo}{{\text{g}}_{4}}\left( x-1 \right)\) là:

A. \(D=\left( 2;+\infty  \right)\).           

B. \(D=\left( 1;2 \right)\).  

C. \(D=\left( 1;2 \right)\cup \left( 2;+\infty  \right)\).          

D. \(D=\left( 1;+\infty  \right)\).

Câu 4. Đồ thị sau là đồ thị của hàm số nào dưới đây?

A. \(y=\frac{x+1}{2x+1}\).

B. \(y=\frac{x-1}{2x+1}\). 

C. \(y=\frac{x}{2x+1}\).    

D. \(y=\frac{x+3}{2x+1}\).

Câu 5. Cho mặt cầu có diện tích bằng \(\frac{8\pi {{a}^{2}}}{3}\). Bán kính mặt cầu bằng:

A. \(\frac{a\sqrt{6}}{3}\). 

B. \(\frac{a\sqrt{3}}{3}\).  

C. \(\frac{a\sqrt{6}}{2}\).  

D. \(\frac{a\sqrt{2}}{3}\).

Câu 6. Hàm số nào dưới đây có đồ thị như trong hình bên ?

A. \(y={{x}^{3}}-3x+1\).    

B. \(y=-{{x}^{2}}+x-1\).     

C. \(y=-{{x}^{3}}+3x+1\). 

D. \(y={{x}^{4}}-{{x}^{2}}+1\).

Câu 7. Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau:

Hàm số \(y=f\left( x \right)\) đồng biến trên khoảng nào dưới đây ?

A. \(\left( -\infty ;0 \right)\).          

B. \(\left( 0;1 \right)\).       

C. \(\left( -1;1 \right)\).    

D. \(\left( 0;+\infty  \right)\).

Câu 8. Cho hàm số có bảng biến thiên như hình bên dưới. Hàm số đã cho đồng biến trên khoảng?

A. \(\left( 0;1 \right)\).       

B. \(\left( -3;+\infty  \right)\).             

C. \(\left( -3;-1 \right)\).    

D. \(\left( 1;+\infty  \right)\).

Câu 9. Tìm tập các giá trị của m để hàm số \(y=\frac{\text{ln}x-m}{m\text{ln}x-4}\) đồng biến trên khoảng \(\left( \text{e};+\infty  \right)\).

A. \(\left( -\infty ;-2 \right)\cup \left( 2;+\infty  \right)\).          

B. \(\left( -\infty ;-2 \right)\cup \left[ 4;+\infty  \right)\).         

C. \(\left( -\infty ;-2 \right)\).    

D. \(\left[ 2;+\infty  \right)\).

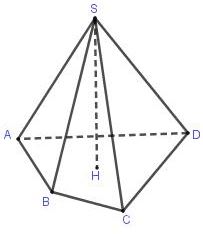
Câu 10. Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt phẳng đáy \(\left( ABC \right)\). Biết SA=a, tam giác ABC là tam giác vuông cân tại A,AB=2a. Tính theo a thể tích V của khối chóp S.ABC.

A. \(V=\frac{{{a}^{3}}}{2}\).                           

B. \(V=2{{a}^{3}}\).          

C. \(V=\frac{{{a}^{3}}}{6}\).      

D. \(V=\frac{2{{a}^{3}}}{3}\).

Câu 11. Cho hình lăng trụ đứng \(ABCD\cdot {A}'{B}'{C}'{D}'\) có đáy là hình thoi, biết \(A{A}'=4a,AC=2a,BD=a\). Thể tích của khối lăng trụ là:

A. \(2{{a}^{3}}\).                

B. \(8{{a}^{3}}\).                

C. \(\frac{8{{a}^{3}}}{3}\).        

D. \(4{{a}^{3}}\).

Câu 12. Gọi l,h,R lần lượt là độ dài đường \(\text{sinh}\), chiều cao và bán kính đáy của một hình nón \(\left( N \right)\). Diện tích toàn phần của hình nón \(\left( N \right)\) là:

A. \({{S}_{TP}}=\pi Rl+\pi {{R}^{2}}\).             

B. \({{S}_{TP}}=2\pi Rl+2\pi {{R}^{2}}\).         

C. \({{S}_{TP}}=\pi Rl+2\pi {{R}^{2}}\).               

D. \({{S}_{TP}}=\pi Rh+\pi {{R}^{2}}\).

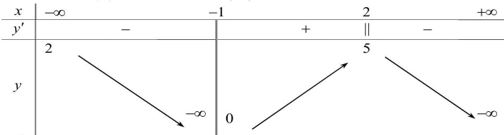
Câu 13. Cho hàm số \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\setminus \left\{ -1 \right\}\) và có bảng biến thiên như sau

Mệnh đề nào dưới đây sai?

A. Đồ thị hàm số \(y=f\left( x \right)\) có 2 đường tiệm cận ngang.

B. Đồ thị hàm số \(y=f\left( x \right)\) có 1 đường tiệm cận đứng.

C. Hàm số đạt đạt cực đại tại x=2.

D. Hàm số có giá trị lớn nhất bằng 5 .

Câu 14. Chọn mệnh đề đúng trong các mệnh đề sau?

A. Hình có đáy là hình bình hành thì có mặt cầu ngoại tiếp.

B. Hình có đáy là hình tứ giác thì có mặt cầu ngoại tiếp.

C. Hình có đáy là hình thang thì có mặt cầu ngoại tiếp.

D. Hình có đáy là hình thang cân thì có mặt cầu ngoại tiếp.

Câu 15. Với a và b là hai số thực dương tùy ý, \(\text{log}\left( a{{b}^{3}} \right)\) bằng:

A. \(\frac{1}{3}\text{log}a+\text{log}b\).         

B. \(\text{log}a+\frac{1}{3}\text{log}b\).          

C. \(\text{log}a+3\text{log}b\).    

D. \(\text{log}a-3\text{log}b\).

............

---(Để xem tiếp nội dung của đề cương các em vui lòng xem tại online hoặc đăng nhập để tải về máy)--- 

Trên đây là một phần nội dung tài liệu Đề cương ôn tập HK1 môn Toán 12 năm học 2022-2023. Để xem thêm nhiều tài liệu tham khảo hữu ích khác các em chọn chức năng xem online hoặc đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.

Mời các em tham khảo tài liệu có liên quan:

• Đề cương ôn tập HK1 môn Lịch Sử 12 năm học 2022-2023
• Đề cương ôn tập HK1 môn Vật lý 12 năm học 2022-2023

Hi vọng tài liệu này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong kì thi sắp tới.

Chúc các em học tốt!