Với mong muốn có thêm tài liệu cung cấp giúp các em học sinh lớp 9 có tài liệu ôn tập rèn luyện chuẩn bị cho kì thi sắp tới. HOC247 giới thiệu đến các em tài liệu Bộ 5 đề thi thử vào lớp 10 môn Toán năm 2022-2023 có đáp án Trường THCS Vĩnh Hưng. Hi vọng tài liệu sẽ giúp ích cho các em có kết quả học tập tốt!
|
TRƯỜNG THCS VĨNH HƯNG |
ĐỀ THI THỬ VÀO LỚP 10 MÔN TOÁN NĂM HỌC 2022 – 2023 Thời gian: 120 phút |
ĐỀ SỐ 1
Câu 1.(1,5 điểm). Cho parabol \(\left( P \right):y=\frac{{{x}^{2}}}{4}\) và đường thẳng \(\left( d \right):y=-\frac{1}{2}x+2\).
a) Vẽ \(\left( P \right)\) và \(\left( d \right)\) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) bằng phép tính.
Câu 2. (1 điểm). Gọi \({{x}_{1}},{{x}_{2}}\) là hai nghiệm của phương trình \(5{{x}^{2}}-3x+2=0\). Không giải phương trình, hãy tính giá trị của biểu thức sau: \(A=\frac{1}{{{x}_{1}}}+\frac{1}{{{x}_{2}}}\)
Câu 3.(1 điểm). Một người đứng tại hai điểm cách 10m nhìn thấy đỉnh tháp với góc nâng lần lượt là \({{40}^{o}}\) và \({{50}^{o}}\). Tính chiều cao của tháp (làm tròn đến mét), biết khoảng cách từ mắt người đó đến mặt đất là 1,6m.
Câu 4.(1 điểm). Để đổi từ nhiệt độ F(Fahrentheit) sang độ C(Celsius), ta dùng công thức sau: \(C=\frac{5}{9}(F-32)\)
a) Hãy tính nhiệt độ C khi biết nhiệt độ F là \({{30}^{o}}F\).
b) Hãy viết biểu thức biểu diễn hàm số bậc nhất F theo biến số C. Tính nhiệt độ F khi biết nhiệt độ C là \({{25}^{o}}C\).
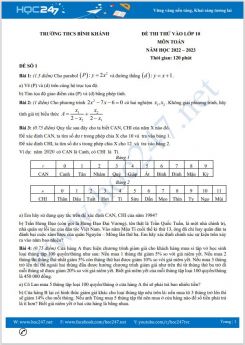
Câu 5.(1 điểm). Cho bảng thống kê điểm trung bình như sau:
Biết số học sinh lớp 9A là 25 em. Tìm số học sinh của hai lớp 9B và 9C.
Câu 6.(1 điểm). Tính diện tích tôn cần thiết để làm một cái thùng hình trụ có chiều cao là 80cm và đáy có diện tích là \(5024c{{m}^{2}}\) (không tính diện tích các chỗ mối ghép và nắp thùng). Lấy \(\pi =3,14.\)
Câu 7.(1 điểm). Một cửa hàng điện máy thực hiện chương trình khuyến mãi giảm giá tất cả
các mặt hàng 10% theo giá niêm yết, và nếu hóa đơn khách hàng trên 10 triệu sẽ được giảm thêm 2% số tiền trên hóa đơn, hóa đơn trên 15 triệu sẽ được giảm thêm 3% số tiền trên hóa đơn, hóa đơn trên 40 triệu sẽ được giảm thêm 6% số tiền trên hóa đơn. Ông An muốn mua một tỉ vi với giá niêm yết là \(9\,\,200\,\,000\) đồng và một tủ lạnh với giá niêm yết là \(8\,\,000\,\,000\) đồng. Hỏi với chương trình khuyến mãi của cửa hàng, ông An phải trã bao nhiêu tiền?
Câu 8.(2,5 điểm) Từ một điểm A nằm ngoài đường tròn \((O;R)\) với \(OA<2R\). Vẽ hai tiếp tuyến AD, AE với (O) (D, E là các tiếp điểm). Gọi H là giao điểm của DE và AO. Lấy điểm M thuộc cung nhỏ DE (M khác D, khác \(E,\,\,MD < ME\)). Tia AM cắt đường tròn (O;R) tại N. Đoạn thẳng AO cắt cung nhỏ DE tại K.
a) Chứng minh \(AO\bot DE\) và \(A{{D}^{2}}=AM.AN\).
b) Chứng minh rằng NK là tia phân giác của góc DNE và tứ giác MHON nội tiếp.
c) Kẻ đường kính KQ của đường tròn (O;R). Tia QN cắt tia ED tại C. Chứng minh \(MD.CE=ME.CD\).
ĐÁP ÁN
Câu 1
a) Vẽ đồ thị \(\left( P \right)\) và \(\left( d \right)\) trên cùng hệ trục tọa độ.
Đồ thị
b) Tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) bằng phép tính.
Phương trình hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\):
\(\begin{array}{l}
\frac{{{x^2}}}{4} = - \frac{1}{2}x + 2\\
\Leftrightarrow \frac{{{x^2}}}{4} + \frac{1}{2}x - 2 = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x = 2\\
x = - 4
\end{array} \right.
\end{array}\)
Thay x=-4 vào \(y=\frac{{{x}^{2}}}{4}\), ta được: \(y=\frac{{{4}^{2}}}{4}=4\).
Thay x=2 vào \(y=\frac{{{x}^{2}}}{4}\), ta được: \(y={{\frac{2}{4}}^{2}}=1\).
Vậy \(\left( -4;\,\,4 \right)\), \(\left( 2;\,\,1 \right)\) là hai giao điểm cần tìm.
---(Để xem tiếp nội dung của đề thi số 1 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---
ĐỀ SỐ 2
ĐỀ THI THỬ VÀO LỚP 10 MÔN TOÁN TRƯỜNG THCS VĨNH HƯNG- ĐỀ 02
Câu 1.(1,5 điểm). Cho parabol \(\left( P \right):y=\frac{{{x}^{2}}}{2}\) và đường thẳng \(\left( d \right):y=-x+4\) .
a) Vẽ đồ thị \(\left( P \right)\) và \(\left( d \right)\) trên cùng hệ trục tọa độ Oxy.
b) Tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) bằng phép tính.
Câu 2. (1 điểm). Cho phương trình \(5{{x}^{2}}-3x-15=0\). Không giải phương trình. Hãy tính giá trị biểu thức \(A={{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}-2{{x}_{1}}-2{{x}_{2}}\) với \({{x}_{1}}\) và \({{x}_{2}}\) là hai nghiệm nếu có của phương trình đã cho.
Câu 3.(0,75 điểm). Một nhà máy sản xuất xi mặng có sản lượng hàng năm được xác định theo hàm số T=12,5n+360. Với T là sản lượng (đơn vị tấn) và n là số năm tính từ năm 2010.
a) Hãy tính sản lượng xi măng của nhà máy vào năm 2020.
b) Theo hàm số trên thì nhà máy đạt sản lượng 510 tấn vào năm nào?
Câu 4.(0,75 điểm). Trong tháng Giêng hai tổ công nhân đã may được 800 chiếc áo. Tháng Hai, tổ 1 may vượt mức 15%, tổ hai may vượt mức 20% so với tháng Giêng do đó cả hai tổ đã may được 945 cái áo. Hỏi trong tháng Giêng mỗi tổ đã may được bao nhiêu chiếc áo?
Câu 5.(1,0 điểm). Trong tháng 4 năm 2021, một công nhân được nhận tiền lương là \(7\,800\,000\) đồng gồm tiền lương trong 24 ngày làm việc bình thường và 4 ngày làm việc đặc biệt (gồm chủ nhật và ngày lễ). Biết tiền lương của một ngày làm việc đặc biệt nhiều hơn tiền lương của một ngày bình thường là \(200\,000\) đồng. Tính tiền lương của một ngày làm việc bình thường.
Câu 6.(1 điểm). Quãng đường giữa hai thành phố A và B dài \(120\,\,km\). Lúc 6 giờ sáng, một ô tô xuất phát từ A đi về B. Người ta thấy mối liên hệ giữa khoảng cách của ô tô so với A và thời điểm đi của ô tô là một hàm số bậc nhất y=ax+b có đồ thị như hình sau:
a) Xác định các hệ số a, b.
b) Lúc 8 giờ sáng ô tô cách B bao xa?
Câu 7.(0,75 điểm). Một cái ly thủy tinh hình nón, bán kính đáy bằng 2cm và chiều cao bằng 6cm
a) Tính thể tích cái ly (biết bề dày của ly không đáng kể) (làm tròn đến chữ số thập phân thứ nhất).
b) Người ta rót rượu vào ly, biết chiều cao của rượu trong ly bằng 3cm. Tính thể tích rượu chứa trong ly. (làm tròn đến chữ số thập phân thứ nhất).
Câu 8.(3 điểm) Cho tam giác ABC nhọn \(\left( AB < AC \right)\). Đường tròn tâm \(\left( O \right)\) đường kính BC cắt AB, AC lần lượt tại E và F. Goi H là giao điểm của BF và CE. Gọi D là giao điểm của AH và BC. Gọi M là trung điểm của HC. Gọi I là giao điểm của DF và CE.
a) Chứng minh \(AH\bot BC\) và \(\widehat{FHC}=\widehat{BAC}\).
b) Chứng minh \(\widehat{FDE}=2\widehat{FCE}\) và IE.IM=ID.IF.
c) Qua I vẽ đường thẳng song song với MF cắt HF, AC lần lượt tại K và S. Lấy T đối xứng với K qua I. Chứng minh tứ giác SHTC nội tiếp.
---(Để xem tiếp nội dung của đề thi số 2 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---
ĐỀ SỐ 3
ĐỀ THI THỬ VÀO LỚP 10 MÔN TOÁN TRƯỜNG THCS VĨNH HƯNG- ĐỀ 03
Bài 1:
a) Giải phương trình \(x(3-4x)=1-2{{x}^{2}}\)
b) Tính hai cạnh góc vuông của một tam giác vuông có cạnh huyền đo được 185m.Biết rằng nếu giảm mỗi cạnh góc vuông 4m thì diện tích tam giác giảm 506 m2.
Bài 2: Cho hai hàm số \(y=\frac{{{x}^{2}}}{4}\) có đồ thị (P) và \(y=\frac{x}{2}+2\) có đồ thị là (d)
a) Vẽ (P) và (d) trên cùng một mặt phẳng tọa độ Oxy.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép toán.
Bài 3: Hình lập phương có thể tích là 125 m3.
a) Tính độ dài d là độ dài đường chéo một mặt của hình lập phương.
b) Tính độ dài D là độ dài đường chéo của hình lập phương.
Bài 4:
Cho phương trình \({{x}^{2}}-2mx+2{{m}^{2}}-1=0\) (1)
(m là tham số; x là ẩn số)
a) Tìm m để phương trình (1) có hai nghiệm dương phân biệt.
b) Tìm để phương trình (1) có hai nghiệm phân biệt \({{x}_{1}}\);\({{x}_{2}}\) thỏa mãn hệ thức \(x_{1}^{3}-x_{1}^{2}+x_{2}^{3}-x_{2}^{2}=2\)
Bài 5: Một đợt bán xe đạp ở cửa hàng sau khi giảm giá lần đầu là 10% và lần thứ hai là 5% thì bây giờ đã tăng 8% trở lại. Biết giá giảm hay tăng giá được tính dựa theo giá đang bán. Hiện tại giá mỗi chiếc xe đạp là 7 387 200 đồng. Tính giá gốc ban đầu khi chưa tăng giảm của đợt bán xe đạp này.
Bài 6: Một chiếc camera có thể tự xoay quanh trục của nó và tầm chiếu tối đa của nó là 5 m.Hãy tính diện tích mà camera có thể quan sát được nếu nó tự quay quanh trục của bản thân với góc quay là 1200.
Bài 7: Một khúc sông rộng khoảng 250m.Một chiếc đò chèo qua sông bị dòng nước đẩy lệch đi một góc 400.Hỏi con đò phải đi thêm bao nhiêu mét nữa so với dự định ban đầu để qua khúc sông ấy?
Bài 8: Cho đường tròn (O;R) và điểm A nằm ngoài đường tròn (O).Vẽ hai tiếp tuyến AB,AC của (O) (B,C :Tiếp điểm).Vẽ cát tuyến ADE của (O) (D.E thuộc (O);D nằm giữa A và E;Tia AD nằm giữa hai tia AB và AO.
a) Chứng minh AB2=AD.AE
b) Gọi H là giao điểm của OA và BC.Chứng minh tứ giác DEOH nội tiếp
c) Đường thẳng AO cắt đường tròn (O) tại M và N (M nằm giữa A và O).
Chứng minh EH.AD = MH.AN
---(Để xem tiếp nội dung của đề thi số 3 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---
ĐỀ SỐ 4
ĐỀ THI THỬ VÀO LỚP 10 MÔN TOÁN TRƯỜNG THCS VĨNH HƯNG- ĐỀ 04
Bài 1. Cho hàm số y = \(\frac{1}{2}{{x}^{2}}\) có đồ thị (P) và hàm số y = \(x+4\) có đồ thị là (D)
a/ Vẽ đồ thị (P) và (D) trên cùng mặt phẳng toạ độ Oxy.
b/ Tìm toạ độ giao điểm của (P) và (D) bằng phép toán.
Bài 2. Biết rằng phương trình bậc hai x2 – 2x + m – 3 = 0 (m là tham số) có hai nghiệm là \({{x}_{1}}\) và \({{x}_{2}}\) . Tính giá trị biểu thức \(H=x_{1}^{2}+x_{2}^{2}-{{x}_{1}}{{x}_{2}}+2019\) theo m.
Bài 3: Một bức tượng cao 1,6 mét được đặt trên một cái bệ. Tại một điểm A trên mặt đất bạn Hào nhìn thấy nóc tượng và nóc bệ với các góc nâng lần lượt là 600 và 450. Tính chiều cao của cái bệ
Bài 4. Một cửa sổ dạng vòm trong hình vẽ gồm phần hình chữ nhật phía dưới và nửa hình tròn phía trên. Phần hình chữ nhật có chiều dài của cạnh đứng là 1m, chiều dài cạnh ngang là 1,2m. Biết giá làm mỗi m2 cửa là 700 000 đồng. Hãy tính giá tiền làm cửa sổ vòm nói trên. (làm tròn đến nghìn đồng)
Bài 5. Thực hiện chương trình khuyến mãi “Ngày Chủ Nhật Vàng”, một cửa hàng điện máy X tổ chức bán hàng giảm giá cho tất cả các sản phẩm điện máy. Một chiếc ti vi được niêm yết giá bán là 12 150 000 đồng, biết rằng giá bán này đã được siêu thị giảm giá 2 lần mỗi lần 10%. Hỏi giá bán chiếc tivi đó của siêu thị khi chưa giảm giá là bao nhiêu?
Bài 6. Ở hai quầy hàng A và B trong hội hoa xuân, người ta bán hai loại bắp rang bơ lần lượt được đựng trong hai loại hộp hình nón và hình trụ với thông tin về giá cả và định lượng như trong hình dưới đây. Vỏ hộp được làm bằng giấy, phần này nhận được tài trợ của công ty giấy, nên cả hai quầy không tốn chi phí làm vỏ hộp. Hỏi bạn H nên mua bắp rang bơ ở quầy A hay quầy B để bạn có lợi hơn? Tại sao?
Bài 7. Từ điểm A nằm ngoài (O), vẽ hai tiếp tuyến AB, AC (B, C là hai tiếp điểm), gọi H là giao điểm của OA và BC. Kẻ đường kính BK của (O), AK cắt (O) tại E
a) Chứng minh: tứ giác OBAC nội tiếp và AB2=AE.AK
b) Chứng minh: tứ giác OHEK nội tiếp và CE \(\bot\) HE.
c) Tia BK và tia AC cắt nhau tại F, kẻ CI \(\bot\) BK (I \(\in\) BK), AK và CI cắt nhau tại M. Gọi N là trung điểm của AB. Chứng minh: ba điểm F, M, N thẳng hàng.
---(Để xem tiếp nội dung của đề thi số 4 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---
ĐỀ SỐ 5
ĐỀ THI THỬ VÀO LỚP 10 MÔN TOÁN TRƯỜNG THCS VĨNH HƯNG- ĐỀ 05
Câu 1. Cho (P): \(y=-\frac{{{x}^{2}}}{4}\) và (D): \(y=-2x+4\)
a) Vẽ đồ thị (P), (d) trên cùng mặt phẳng tọa độ Oxy.
b) Tìm tọa độ giao điểm của (P) và (D).
Câu 2. Cho phương trình: \({{x}^{2}}+2(m+1)x+{{m}^{2}}-2m-5=0\) (1) (x là ẩn số)
a) Tìm m để phương trình (1) có 2 nghiệm \({{x}_{1}}\,,\,{{x}_{2}}\).
b) Tìm m để phương trình (1) có 2 nghiệm \({{x}_{1}}\,,\,{{x}_{2}}\) thỏa \(3{{x}_{1}}+3{{x}_{2}}=-\,\frac{1}{2}{{x}_{1}}.{{x}_{2}}\)
Câu 3. Một địa phương cấy 10ha giống lúa loại I và 8ha giống lúa loại II. Sau một mùa vụ, địa phương đó thu hoạch và tính toán sản lượng thấy:
+ Tổng sản lượng của hai giống lúa thu về là 139 tấn;
+ Sản lượng thu về từ 4ha giống lúa loại I nhiều hơn sản lượng thu về từ 3ha giống lúa loại II là 6 tấn.
Hãy tính năng suất lúa trung bình (đơn vị: tấn/ ha) của mỗi loại giống lúa.
Câu 4. Để khuyến khích tiết kiệm điện, giá điện sinh hoạt được tính theo kiểu lũy tiến, nghĩa là nếu người sử dụng càng dùng nhiều điện thì giá mỗi số điện (1kWh) càng tăng lên theo các mức như sau:
Mức thứ nhất: Tính cho 100 số điện đầu tiền;
Mức thứ hai: Tính cho số điện thứ 101 đến 150, mỗi số đắt hơn 150 đồng so với mức thứ nhất;
Mức thứ ba: Tính cho số điện thứ 151 đến 200, mỗi số đắt hơn 200 đồng so với mức thứ hai; v.v…
Ngoài ra, người sử dụng còn phải trả thêm 10% thuế giá trị gia tăng (thuế VAT).
Tháng vừa qua, nhà Tuấn dùng hết 165 số điện và phải trả 95 700 đồng. Hỏi mỗi số điện ở mức thứ nhất giá là bao nhiêu ?
Câu 5. Trên một khúc sông với 2 bờ song song với nhau, có một chiếc đò dự định chèo qua sông từ vị trí A ở bờ bên này sang vị trí B ở bờ bên kia, đường thẳng AB vuông góc với các bờ sông. Do bị dòng nước đẩy xiên nên chiếc đò đã cập bờ bên kia tại vị tri C cách B mội khoảng bằng 30 m. Biết khúc sông rộng 150 m, hỏi dòng nước đã đẩy chiếc đò lệch đi một góc có số đo bằng bao nhiêu? (kết quả làm tròn đến giây).
Câu 6. Bác Bình gửi tiết kiệm 100 triệu đồng vào ngân hàng A, kì hạn một năm. Cùng ngày, bác gửi tiết kiệm 150 triệu đồng vào ngân hàng B, kì hạn một năm, với lãi suất cao hơn lãi suất của ngân hàng A là 1% / năm. Biết sau đúng 1 năm kể từ ngày gửi tiền. Bác Bình nhận được tổng sổ tiền lãi là 16,5 triệu đồng từ hai khoản tiền gửi tiết kiệm nêu trên. Hỏi lãi suất tiền gửi tiết kiệm kì hạn một năm của ngân hàng A là bao nhiêu phần trăm?
Câu 7. Khi thả chìm hoàn toàn tượng một con ngựa nhỏ bằng đá vào một ly nước có dạng hình trụ thì người ta thấy nước trong ly dâng lên \(1,5\,\text{cm}\) và không tràn ra ngoài. Biết diện tích đáy của ly nước bằng \(80\text{ c}{{\text{m}}^{2}}.\) Hỏi thể tích của tượng ngựa đá bằng bao nhiêu.
Câu 8. Cho hình vuông ABCD có cạnh bằng 6cm. Điểm N nằm trên cạnh CD sao cho DN=2cm, P là điểm nằm trên tia đối của tia BC sao cho BP=DN.
a) Chứng minh \(\Delta ABP=\text{ }\Delta ADN\) và tứ giác ANCP nội tiếp đường tròn.
b) Tính độ dài đường tròn ngoại tiếp tứ giác ANCP.
c) Trên cạnh BC, lấy điểm M sao cho \(\widehat{MAN}=45{}^\circ \). Chứng minh MP=MN và tính diện tích tam giác AMN.
---(Để xem tiếp nội dung của đề thi số 5 các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---
Trên đây là một phần trích đoạn nội dung Bộ 5 đề thi thử vào lớp 10 môn Toán năm 2022-2023 có đáp án Trường THCS Vĩnh Hưng. Để xem toàn bộ nội dung các em chọn chức năng xem online hoặc đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.
Mời các em tham khảo tài liệu có liên quan:
- Bộ 5 đề thi thử vào lớp 10 môn Toán năm 2022-2023 có đáp án Trường THCS Tô Hoàng
- Bộ 5 đề thi thử vào lớp 10 môn Toán năm 2022-2023 có đáp án Trường THCS Tân Lập
Hy vọng bộ đề thi này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong kì thi sắp tới.





.JPG?enablejsapi=1)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)