Giải bài 9 tr 70 sách GK Toán 9 Tập 1
Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và Tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng
a) Tam giác DIL là một tam giác cân;
b) Tổng \(\frac{1}{{D{I^2}}} + \frac{1}{{D{K^2}}}\) không đổi khi I thay đổi trên cạnh AB.
Hướng dẫn giải chi tiết
Bài 9 này ta sẽ áp dụng hệ thức lượng trong tam giác vuông và các định lí hình học để chứng minh bài toán.
.png)
Chứng minh câu a.
Ta có: \(\widehat{ADI}=\widehat{IKB}\) (so le trong)
\(\widehat{CDL}=\widehat{IKB}\) (vì cùng phụ với góc L)
Vậy \(\widehat{CDL}=\widehat{ADI}\)
Xét hai tam giác vuông IAD và LCD có:
\(\widehat{IAD}=\widehat{LCD}=90^o\)
\(AD=CD\)
\(\widehat{CDL}=\widehat{ADI}\)
Vậy \(\Delta IAD=\Delta LCD (g.c.g)\)
\(\Rightarrow ID=DL\)
Vậy tam giác DIL vuông tại D.
Chứng minh câu b.
Ta có:
\(DI=DL\Rightarrow \frac{1}{DI^2}=\frac{1}{DL^2}\)
Xét tam giác DKL vuông tại D có đường cao DC, ta có:
\(\frac{1}{CD^2}=\frac{1}{DL^2}+\frac{1}{DK^2}\)
Theo cmt, ta viết lại là:
\(\frac{1}{CD^2}=\frac{1}{DI^2}+\frac{1}{DK^2}\)
Mà hình vuông ABCD cố định nên CD không đổi, vậy:
\(\frac{1}{DI^2}+\frac{1}{DK^2}\) luôn không đổi khi I thay đổi trên AB!
-- Mod Toán 9 HỌC247
-


Cho tam giác ABC(Â =90 độ) vẽ HE vuông AB(E€AB), vẽ HF vuông góc với AC(F€AC).CMT:A:AB^2=AB,AC^2=HCAB^3=BE.BC,AH^3=BC.CE.CF?
bởi Kim Thuy
 12/09/2020
12/09/2020
 Theo dõi (1) 3 Trả lời
Theo dõi (1) 3 Trả lời -


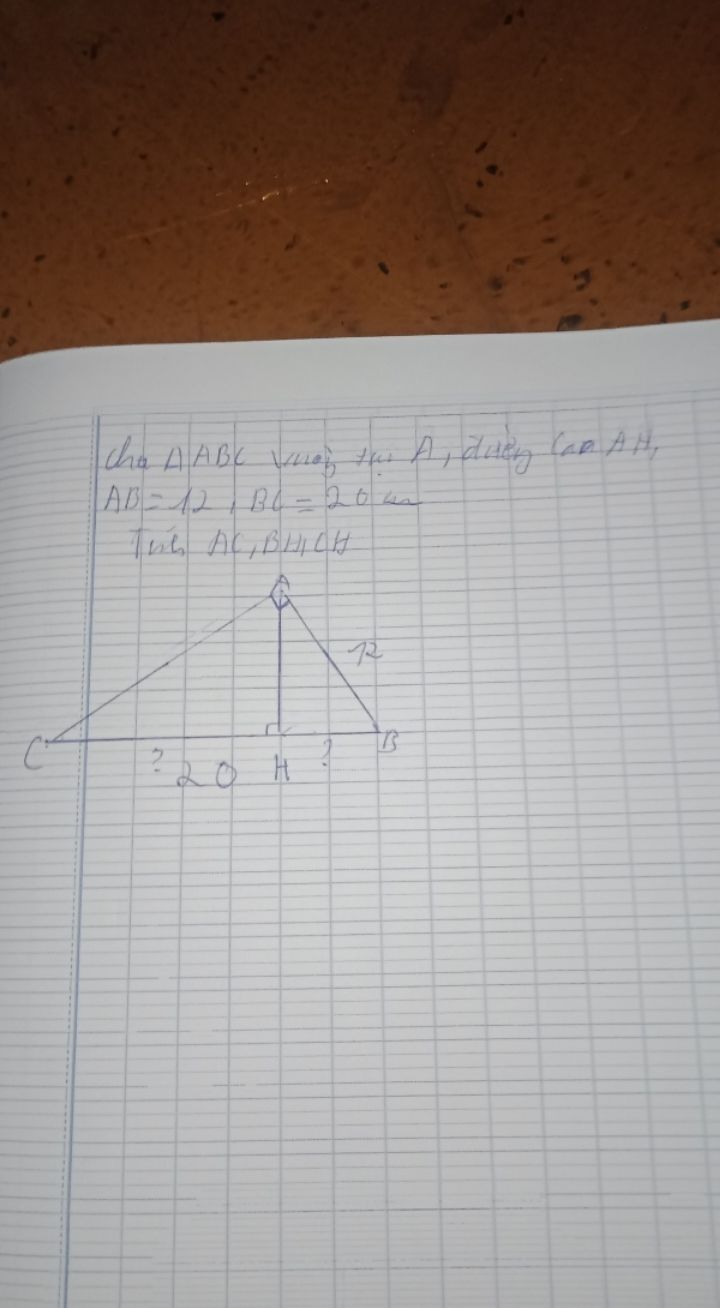 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm x, y ở hình 5
bởi Nguyen Huong
 09/09/2020
09/09/2020
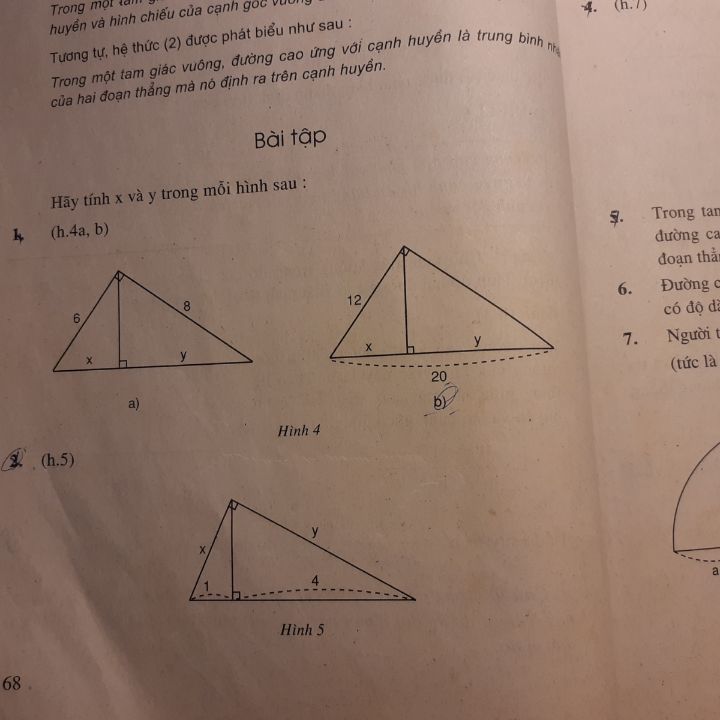 Theo dõi (3) 5 Trả lời
Theo dõi (3) 5 Trả lời
Bài tập SGK khác
Bài tập 7 trang 69 SGK Toán 9 Tập 1
Bài tập 8 trang 70 SGK Toán 9 Tập 1
Bài tập 1 trang 102 SBT Toán 9 Tập 1
Bài tập 2 trang 102 SBT Toán 9 Tập 1
Bài tập 3 trang 103 SBT Toán 9 Tập 1
Bài tập 4 trang 103 SBT Toán 9 Tập 1
Bài tập 5 trang 103 SBT Toán 9 Tập 1
Bài tập 6 trang 103 SBT Toán 9 Tập 1
Bài tập 7 trang 103 SBT Toán 9 Tập 1
Bài tập 8 trang 103 SBT Toán 9 Tập 1
Bài tập 9 trang 104 SBT Toán 9 Tập 1
Bài tập 10 trang 104 SBT Toán 9 Tập 1
Bài tập 11 trang 104 SBT Toán 9 Tập 1
Bài tập 12 trang 104 SBT Toán 9 Tập 1
Bài tập 13 trang 104 SBT Toán 9 Tập 1
Bài tập 14 trang 104 SBT Toán 9 Tập 1
Bài tập 15 trang 104 SBT Toán 9 Tập 1
Bài tập 16 trang 104 SBT Toán 9 Tập 1
Bài tập 17 trang 104 SBT Toán 9 Tập 1
Bài tập 18 trang 105 SBT Toán 9 Tập 1
Bài tập 19 trang 105 SBT Toán 9 Tập 1
Bài tập 20 trang 105 SBT Toán 9 Tập 1
Bài tập 1.1 trang 105 SBT Toán 9 Tập 1
Bài tập 1.2 trang 105 SBT Toán 9 Tập 1
Bài tập 1.3 trang 105 SBT Toán 9 Tập 1
Bài tập 1.4 trang 105 SBT Toán 9 Tập 1
Bài tập 1.5 trang 105 SBT Toán 9 Tập 1
Bài tập 1.6 trang 106 SBT Toán 9 Tập 1
Bài tập 1.7 trang 106 SBT Toán 9 Tập 1
Bài tập 1.8 trang 106 SBT Toán 9 Tập 1





