Giải bài 37 tr 94 sách SGK Toán lớp 9 Tập 1
Cho tam giác ABC có AB = 6cm, AC = 4,5cm, BC = 7,5cm.
a) Chứng minh tam giác ABC vuông tại A. Tính các góc B, C và đường cao AH của tam giác đó.
b) Hỏi rằng điểm M mà diện tích tam giác MBC bằng diện tích tam giác ABC nằm trên đường nào?
Hướng dẫn giải chi tiết
Hướng dẫn giải
+) Chứng minh tam giác có tổng bình phương hai cạnh bằng bình phương cạnh còn lại thì tam giác đó là tam giác vuông.
+) Áp dụng tỉ số lượng giác của góc nhọn để tính các góc của tam giác ABC.
+) Áp dụng hệ thức lượng đối với tam giác vuông có đường cao để tính đường cao của tam giác đó.
+) Diện tích tam giác \(ABC\) vuông tại \(A\): \(S=\dfrac{1}{2}AH.BC=\dfrac{1}{2}AB.AC.\)
Lời giải chi tiết
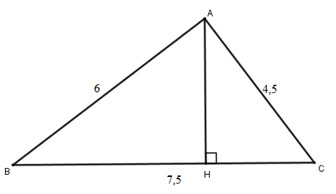
a) Ta có: 62 + 4,52 = 36 + 20,25 = 56,25 = 7,52 = 56,25
∆ABC có AB2 + AC2 = BC2 (=56,25) nên vuông tại A.
\(\eqalign{& tgB = {{AC} \over {AB}} = {{4,5} \over 6} = 0,75 \Rightarrow \widehat B \approx {37^0} \cr & \widehat C = {90^0} - \widehat B \approx {53^0} \cr} \)
∆ABC vuông tại A, AH là đường cao nên:
AH.BC = AB.AC
\(\Rightarrow AH = {{AB.AC} \over {BC}} = {{4,5.6} \over {7,5}} = 3,6(cm)\)
b) SMBC = SABC ⇒ M cách BC một khoảng bằng AH.
Do đó M nằm trên hai đường thẳng song song cách BC một khoảng bằng 3,6 cm
-- Mod Toán 9 HỌC247
-
Bài 95 trang 122 sách bài tập toán 9 tập 1
bởi Thùy Nguyễn
08/10/2018
Bài 95 (Sách bài tập trang 122)Cho tam giác ABC có góc B bằng \(120^0\), BC = 12 cm, AB = 6cm. Đường phân giác của góc B cắt cạnh AC tại D
a) Tính độ dài đường phân giác BD
b) Gọi M là trung điểm của BC. Chứng minh \(AM\perp BD\)
Theo dõi (0) 1 Trả lời -
Bài 2: Tính đến năm 1994, dân số ở thủ đô Hà Nội là 2052116 người. Biết rằng trên đầu mỗi người có không quá 100000 sợi tóc. Chứng minh rằng ở Hà Nội ít ra cũng có 20 người có cùng một số sợi tóc
Theo dõi (0) 1 Trả lời -
Bài 93 trang 121 sách bài tập toán 9 tập 1
bởi Tuấn Huy
08/10/2018
Bài 93 (Sách bài tập trang 121)Cho tam giác ABC, biết AB = 21cm, AC = 28cm, BC = 35cm
a) Chứng minh tam giác ABC vuông
b) Tính sin B, sin C
Theo dõi (0) 1 Trả lời -
Bài 92 trang 121 sách bài tập toán 9 tập 1
bởi Lan Ha
08/10/2018
Bài 92 (Sách bài tập trang 121)Cho tam giác cân ABC, AB = AC = 10 cm, BC = 16. Trên đường cao AH lấy điểm I sao cho \(AI=\dfrac{1}{3}AH\). Vẽ tia Cx song song với AH, Cx cắt tai BI tại D
a) Tính các góc của tam giác ABC
b) Tính diện tích tứ giác ABCD
Theo dõi (0) 1 Trả lời -
Bài 91 trang 121 sách bài tập toán 9 tập 1
bởi Thanh Truc
08/10/2018
Bài 91 (Sách bài tập trang 121)Cho hình thang ABCD có hai cạnh bên là AD và BC bằng nhau, đường chéo AC vuông góc với cạnh bên BC. Biết AD = 5a, AC = 12 a
a) Tính :
\(\dfrac{\sin B+\cos B}{\sin B-\cos B}\)
b) Tính chiều cao của hình thang ABCD
Theo dõi (0) 1 Trả lời -
Bài 90 trang 121 sách bài tập toán 9 tập 1
bởi An Nhiên
08/10/2018
Bài 90 (Sách bài tập trang 121)
Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm
a) Tính \(BC,\widehat{B},\widehat{C}\)
b) Phân giác của góc A cắt BC tại D. Tính BD, CD
c) Từ D kẻ DE và DF lần lượt vuông góc với AB và AC. Tứ giác AEDF là hình gì ? Tính chu vi và diện tích của tứ giác AEDF
Theo dõi (0) 1 Trả lời -
Chứng minh MHIB và MIKC nội tiếp
bởi Lan Ha
31/01/2019
Cho tam giác ABC nội tiếp bên trong đường tròn tâm O . Điểm M di động trên cung nhỏ BC . Từ M kẻ MH MK MI lần lượt vuông góc với AB AC BC
a, chứng minh MHIB và MIKC nội tiếp
b, Chứng minh MB/MH = BC/HK
c, Tìm vị trí của M để độ dài HK lớn nhât
Theo dõi (0) 1 Trả lời -
Bài 89 trang 121 sách bài tập toán 9 tập 1
bởi hi hi
08/10/2018
Bài 89 (Sách bài tập trang 121)Cho hình thanh với đáy nhỏ là 15cm, hai cạnh bên bằng nhau và bằng 25cm, góc tù bằng 120 độ. Tính chu vi và diện tích của hình thang đó ?
Theo dõi (0) 1 Trả lời -
Chứng minh tứ giác DCEF nội tiếp
bởi thùy trang
31/01/2019
Cho tứ giác ABCD nội tiếp đường tròn đường kính AO hai đường chéo AC và BD cắt nhau tại E. Kẻ EF vuông góc vs AD tại F . CMR
a) Tứ giác DCEF nội tiếp
b) góc CDE = góc CEF
c) AF.AD=AE.AC
Theo dõi (0) 1 Trả lời -
Bài 87 trang 120 sách bài tập toán 9 tập 1
bởi Anh Trần
08/10/2018
Bài 87 (Sách bài tập trang 120)Tam giác ABC có \(\widehat{A}=20^0,\widehat{B}=30^0;AB=60cm\). Đường vuông góc kẻ từ C đến AB cắt AB tại P (h.33)
Hãy tìm :
a) AP, BP
b) CP
Theo dõi (0) 1 Trả lời -
Bài 85 trang 120 sách bài tập toán 9 tập 1
bởi Dương Quá
08/10/2018
Bài 85 (Sách bài tập trang 120)Hình 31
Tính góc \(\alpha\) tạo bởi hai mái nhà, biết rằng mỗi mái nhà dài 2,34m và cao 0,8m ?
Theo dõi (0) 1 Trả lời
