Giải bài 41 tr 96 sách SGK Toán lớp 9 Tập 1
Tam giác ABC vuông tại C có AC = 2cm, BC = 5cm, \(\widehat {BAC} = x,\widehat {ABC} = y\). Dùng các thông tin sau (nếu cần) để tìm x – y:
sin 23°36’ ≈ 0,4;
cos66°24’ ≈ 0,4;
tg21°48’ ≈ 0,4
Hướng dẫn giải chi tiết
Hướng dẫn giải
+) Dựa vào các tỉ số lượng giác của góc nhọn.
+) Tổng hai góc nhọn của tam giác bằng \(90^0.\)
Lời giải chi tiết
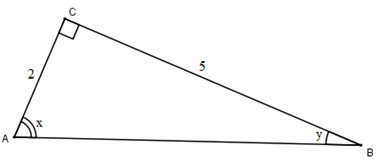
Xét tam giác ABC vuông tại C, theo định nghĩa tỉ số lượng giác của góc nhọn, ta có: \(\displaystyle \tan y =\dfrac{AC}{BC}= {2 \over 5} = 0,4\) nên \(y ≈ 21°48’.\)
Vì tam giác ABC vuông tại C nên \(x+y=90^0\) (tổng hai góc nhọn trong tam giác vuông).
Do đó: \(x = 90° - y ≈ 68°12’.\)
Vậy: \(x – y ≈ 68°12’ - 21°48’ ≈ 46°24’.\)
-- Mod Toán 9 HỌC247
-
Chứng minh 4 điểm A,B,H,K cùng thuộc 1 đường tròn
bởi hà trang
22/02/2019
cho tam giác ABC cân tại A và nội tiếp đường tròn 0 . kẻ các đường cao AH, BK . gọi D là giao điểm thứ 2 của AH và đường tròn O.
1, CM : 4 điểm A,B,H,K cùng thuộc 1 đường tròn
2,CM : CD^2 = DH.AD
3, cho BC=24cm, AC= 20cm. Tính đường cao AH và bán kính đường tròn O
bn nào giải giúp mk với tại mai thi r
Theo dõi (0) 1 Trả lời -
Chứng minh khi cát tuyến MN di động, trung điểm I của MN luôn nằm trên một đường cố định
bởi Hy Vũ
22/02/2019
Cho đường tròn (O) đk AB. Một cát tuyến MN quay quanh trung điểm H của OB.
a. Cm khi cát tuyến MN di động, trung điểm I của MN luôn nằm trên một đường cố định.
b.Từ A kẻ \(Ax\perp MN\). Tia BI cắt Ax tại C. Cm tứ giác BMCN là h.b.h
c. Cm C là trực tâm của \(\Delta AMN\)
d.Khi MN quay xung quanh H thì C di động trên đường nào?
e. Cho AB=2R, \(AM.AN=3R^2\), \(AN=R\sqrt{3}\). Tính diện tích phần hình tròn nằm ngoài tam giác AMN
Theo dõi (0) 1 Trả lời -
Tính BC, BH, AH, AC, biết AB= 6cm, HC= 6,4 cm
bởi Phan Thiện Hải
17/01/2019
Cho tam giác ABC vuông tại A, AH Là đường cao,AB= 6cm, HC= 6,4 cm. Tính BC,BH,AH,AC
Theo dõi (0) 1 Trả lời -
Cho hình thang cân ABCD , đáy lớn AB=13cm, đáy nhỏ CD=5cm, AC vuông góc BC . Diện tích ABCD là...cm
Theo dõi (0) 1 Trả lời -
Chứng minh tứ giác SBOC nội tiếp, OM.OS=R^2
bởi Lê Minh Trí
17/01/2019
Cho tam giác ABC nhọn nội tiếp (O,R), đường ca BE và CF, tiếp tuyến tại B và C cắt nhau tại S. M là giao điểm của BC và OS. Chứng minh
a) Tứ giác SBOC nội tiếp, OM.OS=R^2
b) AF.BC=EF.AC
c) góc AME= ASB
d) AM cắt EF tại N, AS cắt BC tại P. Chứng minh NP vuông góc vói BCTheo dõi (0) 1 Trả lời -
Tính các cạnh tam giác ABC vuông tại A có 2 trung tuyến AM = 6cm, BN=9cm
bởi Ngọc'ss Sunny
03/11/2017
câu 1: tam giác ABC vuông tại A có 2 trung tuyến
AM = 6cm, BN=9cm
tính các cạnh của tam giác ABC
Theo dõi (1) 2 Trả lời
