Giải bài 38 tr 95 sách SGK Toán lớp 9 Tập 1
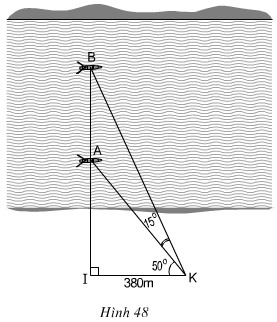
Hai chiếc thuyền A và B ở vị trí được minh họa như trong hình 48. Tính khoảng cách giữa chúng (làm tròn đến mét)
Hướng dẫn giải chi tiết
Hướng dẫn giải
+) Áp dụng: Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tang góc đối.
Lời giải chi tiết
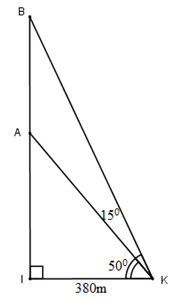
\(\widehat {IKB} = {50^0} + {15^0} = {65^0}\)
∆IBK vuông tại I nên IB = IK. tgIKB = 380 . tg65° ≈ 814,9 (cm)
∆IAK vuông tại I nên IA = IK. tgIKA = 380 . tg50° ≈ 452,9 (cm)
Khoảng cách giữa hai thuyền là: AB = IB – IA ≈ 362 (m)
-- Mod Toán 9 HỌC247
-


Bài 81 trang 119 sách bài tập toán 9 tập 1
bởi Lê Nguyễn Hạ Anh
 08/10/2018
Bài 81 (Sách bài tập trang 119)
08/10/2018
Bài 81 (Sách bài tập trang 119)Hãy đơn giản biểu thức :
a) \(1-\sin^2\alpha\)
b) \(\sin^4\alpha+\cos^4\alpha+2\sin^2\alpha\cos^2\alpha\)
c) \(\left(1-\cos\alpha\right)\left(1+\cos\alpha\right)\)
d) \(tg^2\alpha-\sin^2\alpha.tg^2\alpha\)
e) \(1+\sin^2\alpha+\cos^2\alpha\)
g) \(\cos^2\alpha+tg^2\alpha.\cos^2\alpha\)
h) \(\sin\alpha-\sin\alpha.\cos^2\alpha\)
i) \(tg^2\alpha\left(2\cos^2\alpha+\sin^2\alpha-1\right)\)
Theo dõi (0) 1 Trả lời -


Chứng minh OI vuông góc với AB và OI song song với BC
bởi thủy tiên
 31/01/2019
31/01/2019
Cho (O;R) có đường kính AC. TRên tiếp tuyến tại A của (O), lấy I sao cho AI>R. Từ I vẽ tiếp tuyến IB của (O) với B là tiếp điểm (A khác B).
a) Cm: OI vuông góc với AB và OI song song với BC.
b) Kẻ BK vuông góc với AC tại k. Cm: BC.BI=OI.KB
c) Qua O vẽ đường thẳng d vuông góc với AC. Gọi H là hình chiếu của I trên D. Cm: 3 điểm H,B,C thẳng hàng
d) Đoạn thẳng IO cắt (O) và AB lần lượt tại M và N. Cm: cos AIO=\(\frac{MN}{AN}\) +\(\frac{MN}{AI}\)
Theo dõi (0) 1 Trả lời -


Chứng minh B, C, E, F cùng thuộc 1 nửa đường tròn
bởi A La
 31/01/2019
31/01/2019
Cho tam giác ABC nội tiếp đường tròn (O, R). Kẻ đường cao BE, CF lần lượt cắt (O) tại P và Q.
a, Chứng minh: B, C, E, F cùng thuộc 1 nửa đường tròn
b, EFPQ là hình gì?
c, OA vuông góc với EF
d, Kẻ AH cắt BC và (O) lần lượt tại D và N. Chứng minh bán kính đường tròn ngoại tiếp tam giác BHC = R.
Theo dõi (0) 1 Trả lời -


Chứng minh rằng tứ giác ABEF nội tiếp đường tròn
bởi minh thuận
 31/01/2019
31/01/2019
cho tứ giác ABCD nội tiếp nửa đường tròn đường kính AD. hai đường chéo AC và BD cắt nhau tại E . kẻ EF vuông góc AD . gọi M là trtung điễm của AE . chứng minh rằng
a, tứ giác ABEF nội tiếp đường tròn
b, Tia BD là tia phân giác của góc CBF
c, tứ giác BMFC nội tiếp đường tròn
Theo dõi (0) 1 Trả lời -


Chứng minh OM vuông góc với BC
bởi bach hao
 31/01/2019
31/01/2019
cho tam giác ABC nội tiếp (O; R), tia phân giác của \(\widehat{BAC}\) cắt BC tại I, cắt đường tròn tại M
1) chứng minh OM vuông góc với BC
2) chứng minh \(MC^2=MC.MA\)
3) Kẻ đường kính MN, các tia phân giác của góc B và C cắt đường thẳng AN tại P và Q. Chứng minh bốn điểm P, C, B, Q cùng thuộc một đường tròn.
Còn câu 3 mình không làm được :(((
Theo dõi (0) 1 Trả lời -


Chứng minh BC/MD=CA/MH+AB/MK
bởi minh dương
 31/01/2019
31/01/2019
cho (O) ngoại tiếp tam giác ABC, từ M trên cung BC không chứa A, hạ các đường vuông góc đến BC,CA,AB lần lượt tại D,H,K. cm \(\frac{BC}{MD}=\frac{CA}{MH}+\frac{AB}{MK}\)
Theo dõi (0) 1 Trả lời -


Tam giác vuông có cạnh góc vuông bằng 20 và bán kính đường tròn nội tiếp bằng 6
bởi thùy trang
 31/01/2019
31/01/2019
Tam giác vuông có cạnh góc vuông bằng 20 và bán kính đường tròn nội tiếp bằng 6.Tính diện tích tam giác đó ?
Theo dõi (0) 1 Trả lời -


Tính đường cao AH, có B=55 độ , BC=40cm
bởi Naru to
 22/02/2019
22/02/2019
Cho tam giác ABC vuông tại A có B=55 độ , BC=40cm . TÍnh đường cao AH
Theo dõi (0) 1 Trả lời -


Chứng minh A là trực tâm của tam giác BEF
bởi Nguyễn Sơn Ca
 22/02/2019
22/02/2019
Cho đường tròn (O) đường kính AB=2R.Trên tia đối của tia AB lấy M sao cho AM=R.Từ M kẻ đường thẳng d vuông góc với BM . gọi N là trung điểm của OA . qua N vẽ dây cung CD của đường tròn .tia BC cắt d tại E, tia BD cát d tại F
chứng minh A là trực tâm của tam giác BEF
Theo dõi (0) 1 Trả lời -


Chứng minh rằng tứ giác AFHE là hình chữ nhật
bởi hồng trang
 22/02/2019
22/02/2019
Cho tam giác ABC vuông góc với A ( AB > AC), đường cao AH . Trên nửa mặt phẳng bờ BC chưa điểm A vẽ nửa đường tròn đường kính BH cắt AB tại E, nửa đường tròn đường kính HC, cắt AC tại F. Chứng minh rằng :
a) Tứ giác AFHE là hình chữ nhật
b) Tứ giác BEFC là tứ iasc nội tiếp đường tròn
c) EF là tiếp truyến chung của hai nửa đường tròn đường kính BH và HC
Theo dõi (0) 1 Trả lời -


Chứng minh rằng NE vuông góc với AB
bởi Tieu Dong
 22/02/2019
22/02/2019
Cho đường tròn (O) , đường kính AB, điểm M thuộc đường tròn. Vẽ điểm N đối xứng với A qua M. BN cắt đường tròn ở C. Gọi E là giao điểm của AC và BM.
A)cmr:NE vuông góc với AB
B)Gọi F là điểm đối xứng với E qua M.CM: FA là tiếp tuyến của (O)
C)CM: NF là tiếp tuyến của đường tròn(B;BA)
D)CM:BM.BF=BF2-NF2
Theo dõi (0) 1 Trả lời





