Giải bài 37 tr 57 sách BT Toán lớp 9 Tập 2
Tính nhẩm nghiệm của phương trình:
a) \(7{x^2} - 9x + 2 = 0\)
b) \(23{x^2} - 9x - 32 = 0\)
c) \(1975{x^2} + 4x - 1979 = 0\)
d) \(\left( {5 + \sqrt 2 } \right){x^2} + \left( {5 - \sqrt 2 } \right)x - 10 = 0\)
e) \({1 \over 3}{x^2} - {3 \over 2}x - {{11} \over 6} = 0\)
f) \(31,1{x^2} - 50,9x + 19,8 = 0\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Áp dụng:
- Nếu phương trình \(a{x^2} + bx + c = 0\,(a \ne 0)\) có \(a + b + c = 0\) thì phương trình có một nghiệm \({x_1}= 1\), còn nghiệm kia là \({x_2}=\dfrac{c}{a}.\)
- Nếu phương trình \(a{x^2} + bx + c = 0\,(a \ne 0)\) có \(a - b + c = 0\) thì phương trình có nghiệm là \({x_1}= -1\), còn nghiệm kia là \({x_2}=\dfrac{-c}{a}\).
Lời giải chi tiết
a) \(7{x^2} - 9x + 2 = 0\)
Ta có hệ số: a = 7, b = -9, c = 2
Phương trình có dạng: a + b + c = 0
\(\Rightarrow 7 + \left( { - 9} \right) + 2 = 0 \Rightarrow {x_1} = 1;{x_2} = {2 \over 7}\)
b) \(23{x^2} - 9x - 32 = 0\)
Ta có hệ số: a = 23, b = -9, c = -32
Phương trình có dạng: a – b + c = 0
\(\eqalign{
& \Rightarrow 23 - \left( { - 9} \right) + \left( { - 32} \right) = 23 + 9 - 32 = 0 \cr
& {x_1} = - 1;{x_2} = - {{ - 32} \over {23}} = {{32} \over {23}} \cr} \)
c) \(1975{x^2} + 4x - 1979 = 0\)
Ta có hệ số: a = 1975, b = 4, c = -1979
Phương trình có dạng: \(a + b + c = 0\)
\(\eqalign{
& \Rightarrow 1975 + 4 + \left( { - 1979} \right) = 0 \cr
& {x_1} = 1;{x_2} = {{ - 1979} \over {1975}} \cr} \)
d) \(\left( {5 + \sqrt 2 } \right){x^2} + \left( {5 - \sqrt 2 } \right)x - 10 = 0\)
Ta có hệ số \(a = 5 + \sqrt 2 ,b = 5 - \sqrt 2 ,c = - 10\)
Phương trình có dạng: \(a + b + c = 0\)
\(\eqalign{
& \Rightarrow 5 + \sqrt 2 + 5 - \sqrt 2 + \left( { - 10} \right) = 0 \cr
& {x_1} = 2;{x_2} = {{ - 10} \over {5 + \sqrt 2 }} = - {{10\left( {5 - \sqrt 2 } \right)} \over {23}} \cr} \)
e) \({1 \over 3}{x^2} - {3 \over 2}x - {{11} \over 6} = 0\)
Ta có hệ số: \(a = {1 \over 3},b = - {3 \over 2},c = - {{11} \over 6}\)
Phương trình có dạng: \(a - b + c = 0\)
\(\eqalign{
& \Rightarrow {1 \over 3} - \left( { - {3 \over 2}} \right) + \left( { - {{11} \over 6}} \right) = {1 \over 3} + {3 \over 2} - {{11} \over 6} = {2 \over 6} + {9 \over 6} - {{11} \over 6} = 0 \cr
& {x_1} = 1;{x_2} = - {{ - 11} \over 6}:{1 \over 3} = {{11} \over 6}.{3 \over 1} = {{11} \over 2} \cr} \)
f) \(31,1{x^2} - 50,9x + 19,8 = 0\)
Ta có hệ số: a = 31,1; b = -50,9; c = 19,8
Phương trình có dạng: \(a + b + c = 0\)
\(\eqalign{
& \Rightarrow 31,1 + \left( { - 50,9} \right) + 19,8 = 0 \cr
& {x_1} = 1;{x_2} = {{19,8} \over {31,1}} = {{198} \over {311}} \cr} \)
-- Mod Toán 9 HỌC247
-


Tìm để phương trình 5x^2+mx-28=0 có 2 nghiệm thoả mãn 5x1+2x2=1
Theo dõi (0) 0 Trả lời -


Mọi người giúp em câu b bài 3 với ạ
Mọi người cố gắng giúp em nhé. Em cảm ơn mọi người.
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


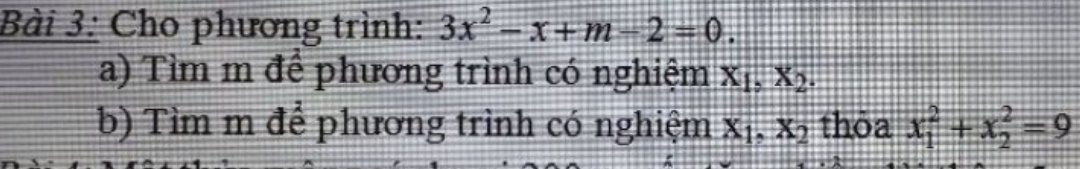 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Cho pt -x² +2x +5 =0. Không giải phương trình chứng tỏ pt luôn có 2 nghiệm phân biệt?
bởi Phan Minh Hải
 01/05/2020
Hệ thức vi ét và ung dụng của phần bài tập hãy giúp mình nhé các bạnTheo dõi (0) 2 Trả lời
01/05/2020
Hệ thức vi ét và ung dụng của phần bài tập hãy giúp mình nhé các bạnTheo dõi (0) 2 Trả lời -


Tìm giá trị m thỏa mãn bài toán?
bởi Nguyen Bao Tran
 30/04/2020
30/04/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải phương trình x^2-(2m+1)x+m^2-1=0 với m=2
bởi Khánh Linh
 26/04/2020
26/04/2020
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm m để phương trình x^2-2x 3-m=0 có nghiệm
bởi Trangg Thùy
 25/04/2020
25/04/2020
cho phương trình x^2-2x 3-m=0 (ẩn x,tham số m) a, định m để phương trình có nghiệm b,định m để phương trình có 1 nghiệm là 2? tìm nghiệm còn lại? c, định m để phương trình có 2 nghiệm trái dấu
Theo dõi (1) 0 Trả lời -


Lập phương trình bậc 2 có 2 nghiệm 1/x1 và 1/x2
bởi Phanh Đinh
 21/04/2020
Giúp em bài này với ạ
21/04/2020
Giúp em bài này với ạ Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Mong mọi người giúp đỡ ạ!
Mong mọi người giúp đỡ ạ! Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Chứng minh phương trình x^2-2mx+m^2+m-2=0 có hai nghiệm phân biệt với mọi m
bởi Hồng Ngọcc
 21/04/2020
Giúp em với
21/04/2020
Giúp em với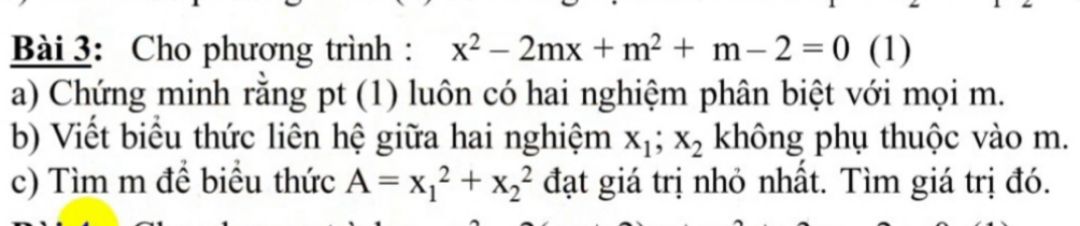 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm m để phương trình x^2 - (m-2)x m 5=0 có 2 nghiệm x1, x2 thỏa mãn x1^2+ x2^2=10
bởi Cô Bé Mùa Đông
 19/04/2020
m để phương trình x^2 - (m-2)x m 5=0 có 2 nghiệm x1,x2 thoa mãn x12 x22=10Theo dõi (0) 0 Trả lời
19/04/2020
m để phương trình x^2 - (m-2)x m 5=0 có 2 nghiệm x1,x2 thoa mãn x12 x22=10Theo dõi (0) 0 Trả lời -


Tìm m để phương trình x^2-2mx+2m-1=0 có nghiệm kép và tính nghiệm đó
bởi Huỳnh Nguyễn Thảo Vy
 16/04/2020
cho phương trình bậc nhất 2 ẩn (ẩn x): x²-2mx 2m-1=0 .Xác định m để phương trình có nghiệm kép và tính nghiệm đó.Theo dõi (1) 0 Trả lời
16/04/2020
cho phương trình bậc nhất 2 ẩn (ẩn x): x²-2mx 2m-1=0 .Xác định m để phương trình có nghiệm kép và tính nghiệm đó.Theo dõi (1) 0 Trả lời -


 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Giải hệ phương trình x+3y=4 và 3x-4y=-1
bởi Linh Thuỳ
 12/04/2020
12/04/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Cho pt: x^2 - 2mx -1=0Tìm m thỏa mãn: x1^2 x2^2 = x1^2*x2^2 2Mong các bạn giúp mik nhaTheo dõi (0) 2 Trả lời
Cho pt: x^2 - 2mx -1=0Tìm m thỏa mãn: x1^2 x2^2 = x1^2*x2^2 2Mong các bạn giúp mik nhaTheo dõi (0) 2 Trả lời -


Tìm 2 số a và b biết a b=9 và a^2 b^2=41
bởi Bảo Long
 07/04/2020
Tìm 2 số a và b biết a b=9 và a^2 b^2=41Theo dõi (0) 3 Trả lời
07/04/2020
Tìm 2 số a và b biết a b=9 và a^2 b^2=41Theo dõi (0) 3 Trả lời -


Tìm m để phương trình x^2-2(m-1)x m^2=0 có 2 nghiệm phân biệt x1,x2 thảo mãn (x1-x2)^2 -6m = x1-2x2
bởi Hi Hoa
 05/04/2020
PT x^2-2(m-1)x m^2=0 có 2 nghiệm phân biệt x1,x2 thảo mãn (x1-x2)^2 -6m = x1-2x2Theo dõi (0) 3 Trả lời
05/04/2020
PT x^2-2(m-1)x m^2=0 có 2 nghiệm phân biệt x1,x2 thảo mãn (x1-x2)^2 -6m = x1-2x2Theo dõi (0) 3 Trả lời
Bài tập SGK khác
Bài tập 35 trang 57 SBT Toán 9 Tập 2
Bài tập 36 trang 57 SBT Toán 9 Tập 2
Bài tập 38 trang 57 SBT Toán 9 Tập 2
Bài tập 39 trang 57 SBT Toán 9 Tập 2
Bài tập 40 trang 57 SBT Toán 9 Tập 2
Bài tập 41 trang 58 SBT Toán 9 Tập 2
Bài tập 42 trang 58 SBT Toán 9 Tập 2
Bài tập 43 trang 58 SBT Toán 9 Tập 2
Bài tập 44 trang 58 SBT Toán 9 Tập 2
Bài tập 6.1 trang 58 SBT Toán 9 Tập 2
Bài tập 6.1 trang 58 SBT Toán 9 Tập 2





