Giải bài 18 tr 16 sách GK Toán 9 Tập 2
a) Xác định các hệ số a và b, biết rằng hệ phương trình
\(\left\{\begin{matrix} 2x + by=-4 & & \\ bx - ay=-5& & \end{matrix}\right.\)
Có nghiệm là \((1; -2)\)
b) Cũng hỏi như vậy, nếu hệ phương trình có nghiệm là \((\sqrt{2}-1; \sqrt{2})\)
Hướng dẫn giải chi tiết bài 18
a) Hệ phương trình có nghiệm là \((1; -2)\) khi và chỉ khi \((1; -2)\) thỏa mãn hệ phương trình. Thay \(x=1,\ y=-2\) vào hệ, ta có:
\(\left\{\begin{matrix} 2 - 2b=-4 & & \\ b+2a=-5 & & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} 2b=6 & & \\ b+2a=-5 & & \end{matrix}\right. \)
\( \Leftrightarrow \left\{\begin{matrix} b=3 & & \\ b+2a=-5 & & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} b=3 & & \\ 3+2a=-5 & & \end{matrix}\right. \)
\(\Leftrightarrow \left\{\begin{matrix} b=3 & & \\ 2a = -5 - 3& & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} b=3 & & \\ 2a = -8& & \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} b=3 & & \\ a = -4 & & \end{matrix}\right.\)
Vậy \(a=-4,\ b=3\) thì hệ có nghiệm là \((1; -2)\).
b) Thay \(x=\sqrt 2 - 1;\ y= \sqrt 2\) vào hệ phương trình đã cho, ta có:
\(\left\{\begin{matrix} 2(\sqrt{2}-1)+b\sqrt{2}= -4 & & \\ (\sqrt{2}-1)b - a\sqrt{2}= -5& & \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} 2\sqrt{2}-2+b\sqrt{2}= -4 & & \\ (\sqrt{2}-1)b - a\sqrt{2}= -5& & \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} 2\sqrt{2}-2+b\sqrt{2}= -4 & & \\ (\sqrt{2}-1)b - a\sqrt{2}= -5& & \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} b\sqrt{2}= -2 - 2\sqrt{2} & & \\ (\sqrt{2}-1)b - a\sqrt{2}= -5& & \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} b= -(2 + \sqrt{2}) & & \\ a\sqrt{2}= -(2 + \sqrt{2})(\sqrt{2}-1)+5& & \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} b= -(2 + \sqrt{2}) & & \\ a\sqrt{2}= -\sqrt{2}+5& & \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} a = \dfrac{-2+5\sqrt{2}}{2} & & \\ b = -(2+ \sqrt{2})& & \end{matrix}\right.\)
Vậy \(a = \dfrac{-2+5\sqrt{2}}{2},\ b=-(2+ \sqrt{2})\) thì hệ trên có nghiệm là \((\sqrt 2 -1; \sqrt 2)\).
-- Mod Toán 9 HỌC247
-


Giải hệ phương trình 2x+4=0 và 4x+2y=-3
bởi Naa' Nguyễnn'
 28/04/2020
28/04/2020
 Theo dõi (1) 3 Trả lời
Theo dõi (1) 3 Trả lời -


Giải hệ phương trình bằng phương pháp đặt ẩn phụ
bởi Quỳnh Trần
 27/04/2020
27/04/2020
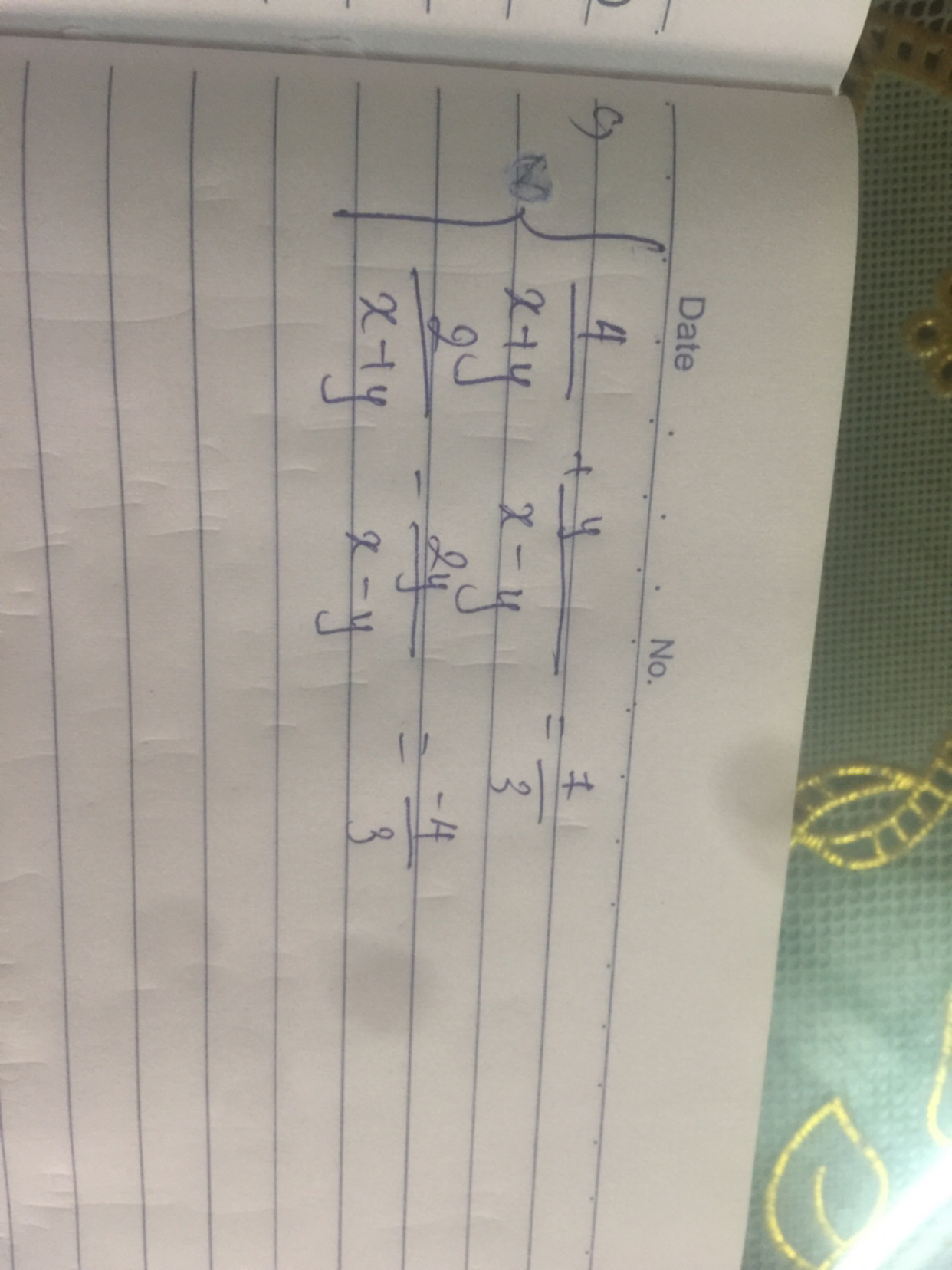 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Giải hệ phương trình x+y=46 và x-y=6
bởi Thào Thị Nú
 21/04/2020
Giải hệ phương trình
21/04/2020
Giải hệ phương trình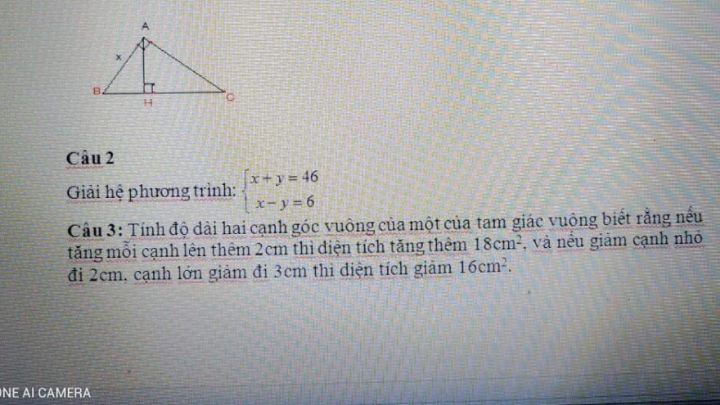 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Giải hệ phương trình 7x+4y=18 và 3x-4y=2
bởi Thùy Thanh
 16/04/2020
16/04/2020
Giải hệ phương trình 7x+4y=18 và 3x-4y=2
Theo dõi (1) 0 Trả lời -


Giải hệ phương trình x+y=3 và x-y=1
bởi Thư Thư
 15/04/2020
Giúp tui giải câu 1 với
15/04/2020
Giúp tui giải câu 1 với Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải hệ phương trình 4x-2y=3 và 6x-3y=5
bởi Ngân Chi
 11/04/2020
11/04/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Giải hệ phương trình -5x+2y=4 và 6x-3y=7
bởi lê nguyễn hồng phúc
 07/04/2020
07/04/2020
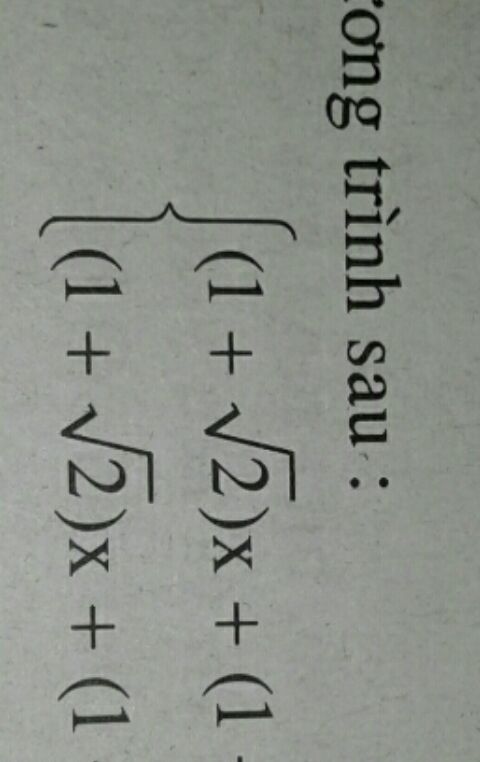 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Giải hệ phương trình 10x-9y=1 và 15x+21y=36
bởi Thu Hiền
 31/03/2020
Giải giúp mình vs
31/03/2020
Giải giúp mình vs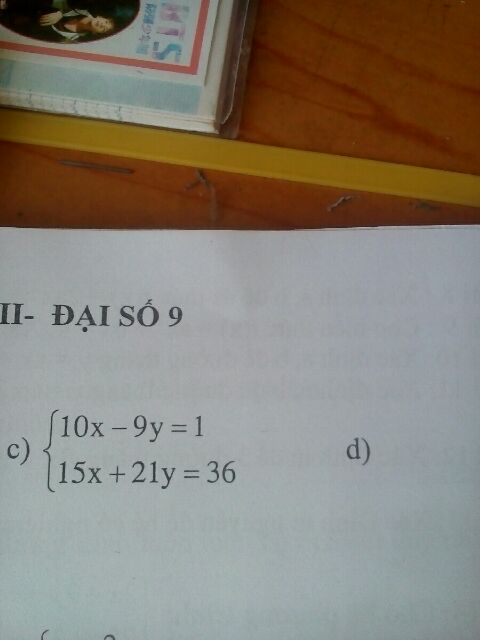 Theo dõi (1) 12 Trả lời
Theo dõi (1) 12 Trả lời -


Giải hệ phương trình x/y=1/3 và x+y=12
bởi Tám Dương
 20/03/2020
20/03/2020
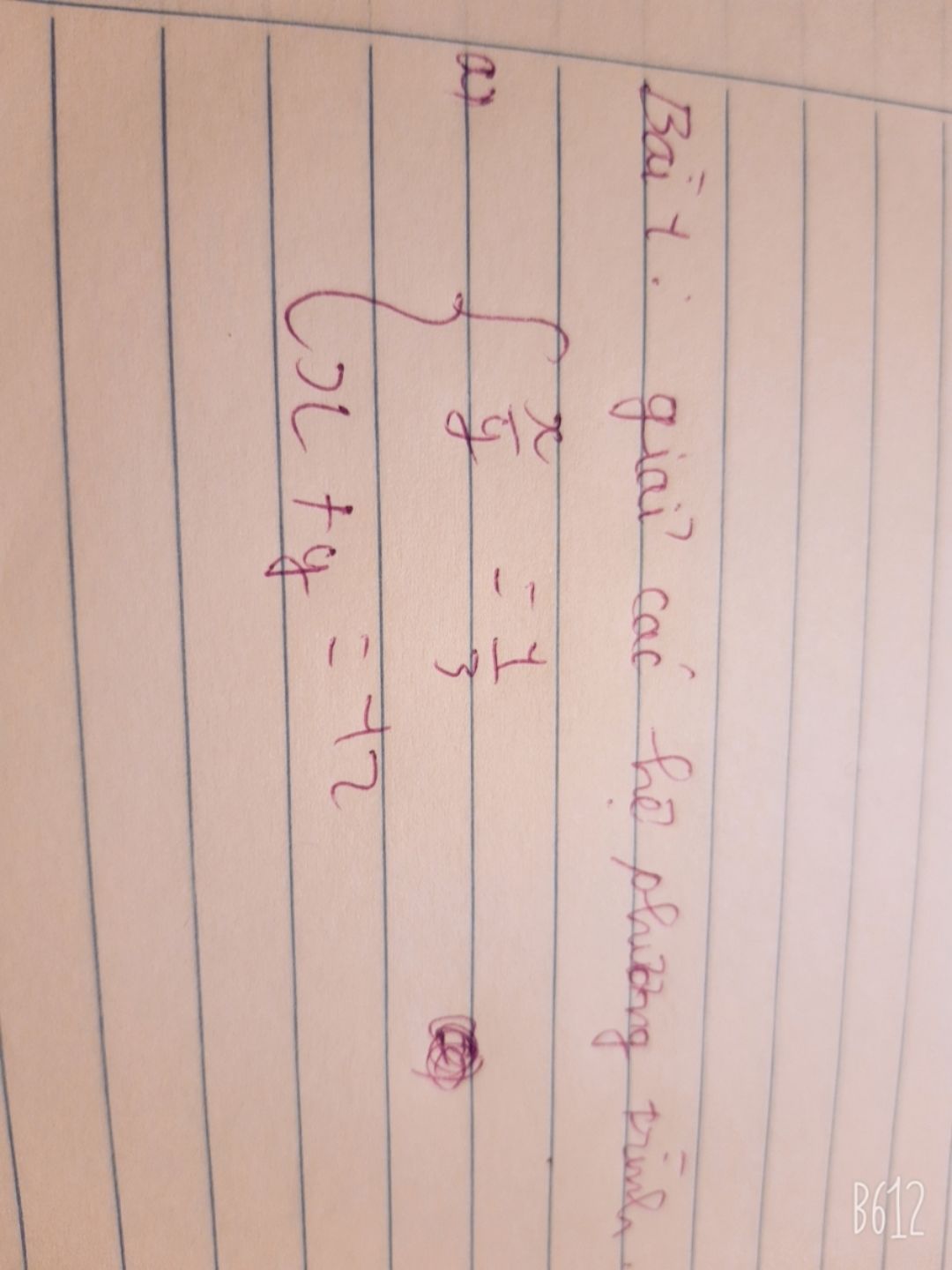 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Một người mua tám cái bánh và bốn chai nước, tổng số tiền phải trả là 128 nghìn đồng. Biết rằng giá mỗi cái bánh gấp 1,5 lần giá một chai nưc. Tính giá mội cái bánh.
bởi Hắc Lục Tử Huy
 19/03/2020
16/Một người mua tám cái bánh và bốn chai nước , tổng số tiền phải trả là 128 nghìn đồng . Biết rằng giá mỗi cái bánh gấp 1,5 lần giá một chai nước . Tính giá mội cái bánhTheo dõi (0) 3 Trả lời
19/03/2020
16/Một người mua tám cái bánh và bốn chai nước , tổng số tiền phải trả là 128 nghìn đồng . Biết rằng giá mỗi cái bánh gấp 1,5 lần giá một chai nước . Tính giá mội cái bánhTheo dõi (0) 3 Trả lời -


Số học sinh giỏi và khá học kì I của trường THCS A là 433 em, mỗi học sinh giỏi được thưởng 8 quyển vở, mỗi học sinh khá được thưởng 5 quyển vở. Tổng số vở phát thưởng là 3119 quyển. Tính số học sinh giỏi và học sinh tiên tiến của trường?
bởi Nguyễn Văn Sỹ
 11/03/2020
11/03/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Cho hệ phương trình mx + y =2 và x+ my =2. Giải hệ phương trình khi m=-1/2 . Tìm m để hệ phương trình vô nghiệm? Có nghiệm duy nhất?vô số nghiệm?
bởi Nga Nguyễn
 27/02/2020
Giúp e vsTheo dõi (0) 0 Trả lời
27/02/2020
Giúp e vsTheo dõi (0) 0 Trả lời -


 Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -


 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 16 trang 16 SGK Toán 9 Tập 2
Bài tập 17 trang 16 SGK Toán 9 Tập 2
Bài tập 19 trang 16 SGK Toán 9 Tập 2
Bài tập 16 trang 9 SBT Toán 9 Tập 2
Bài tập 17 trang 9 SBT Toán 9 Tập 2
Bài tập 18 trang 9 SBT Toán 9 Tập 2
Bài tập 19 trang 9 SBT Toán 9 Tập 2
Bài tập 20 trang 9 SBT Toán 9 Tập 2
Bài tập 21 trang 9 SBT Toán 9 Tập 2
Bài tập 22 trang 10 SBT Toán 9 Tập 2
Bài tập 23 trang 10 SBT Toán 9 Tập 2
Bài tập 24 trang 10 SBT Toán 9 Tập 2





