Giải bài 17 tr 16 sách GK Toán 9 Tập 2
Giải hệ phương trình sau bằng phương pháp thế.
a) \(\left\{\begin{matrix} x\sqrt{2}- y \sqrt{3}=1 & & \\ x + y\sqrt{3} = \sqrt{2}& & \end{matrix}\right.\)
b) \(\left\{\begin{matrix} x - 2\sqrt{2} y = \sqrt{5}& & \\ x\sqrt{2} + y = 1 - \sqrt{10}& & \end{matrix}\right.\)
c) \(\left\{\begin{matrix} (\sqrt{2}- 1)x - y = \sqrt{2}& & \\ x + (\sqrt{2}+ 1)y = 1& & \end{matrix}\right.\)
Hướng dẫn giải chi tiết bài 17
Câu a:
Ta có:
\(\left\{ \matrix{
x\sqrt 2 - y\sqrt 3 = 1 \hfill \cr
x + y\sqrt 3 = \sqrt 2 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x\sqrt 2 - y\sqrt 3 = 1 \hfill \cr
x = \sqrt 2 - y\sqrt 3 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
\left( {\sqrt 2-y\sqrt 3 } \right)\sqrt 2 - y\sqrt 3 = 1 \ (1) \hfill \cr
x = \sqrt 2 - y\sqrt 3 \ (2) \hfill \cr} \right.\)
Giải phương trình \((1)\), ta được:
\(( \sqrt 2 - y\sqrt 3)\sqrt 2 - y\sqrt 3 = 1\)
\( \Leftrightarrow (\sqrt 2)^2 - y\sqrt 3 . \sqrt 2 - y\sqrt 3 = 1 \)
\( \Leftrightarrow 2 - y\sqrt 3 . \sqrt 2 - y\sqrt 3 = 1 \)
\( \Leftrightarrow -y\sqrt 3. \sqrt 2 - y\sqrt 3 = 1 - 2\)
\(\begin{array}{l}
\Leftrightarrow - y\sqrt 6 - y\sqrt 3 = - 1\\
\Leftrightarrow y\left( {\sqrt 6 + \sqrt 3 } \right) = 1\\
\Leftrightarrow y = \dfrac{1}{{\sqrt 6 + \sqrt 3 }}\\
\Leftrightarrow y = \dfrac{{\sqrt 6 - \sqrt 3 }}{3}\\
\Leftrightarrow y = \dfrac{{\sqrt 3 \left( {\sqrt 2 - 1} \right)}}{3}
\end{array}\)
Thay \(y\) tìm được vào phương trình \((2)\), ta được:
\(x = \sqrt 2 - \dfrac{\sqrt 3 (\sqrt 2 -1)}{3}.\sqrt 3\)
\( \Leftrightarrow x=\sqrt 2 - \dfrac{\sqrt 3 .\sqrt 3(\sqrt 2 -1)}{3} \)
\(\Leftrightarrow x=\sqrt 2 - \dfrac{ 3(\sqrt 2 -1)}{3} =\sqrt 2 - (\sqrt 2 -1) \)
\(\Leftrightarrow x=\sqrt 2 -\sqrt 2 +1=1.\)
Vậy hệ phương trình đã cho có nghiệm duy nhất là: \( {\left( 1;\dfrac{\sqrt 3 (\sqrt 2 -1)}{3} \right)}\)
Câu b:
Ta có:
\(\left\{ \matrix{
x - 2\sqrt 2 y = \sqrt 5 \hfill \cr
x\sqrt 2 + y = 1 - \sqrt {10} \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
x = 2\sqrt 2 y + \sqrt 5 \ (1) \hfill \cr
\left( {2\sqrt 2 y + \sqrt 5 } \right).\sqrt 2 + y = 1 - \sqrt {10}\ (2) \hfill \cr} \right.\)
Giải phương trình \((2)\), ta được:
\(\left( {2\sqrt 2 y + \sqrt 5 } \right).\sqrt 2 + y = 1 - \sqrt {10}\)
\(\Leftrightarrow 2(\sqrt 2 .\sqrt 2)y + \sqrt 5 .\sqrt 2 + y = 1 - \sqrt {10}\)
\(\Leftrightarrow 4y + \sqrt{10}+y=1- \sqrt{10}\)
\(\Leftrightarrow 4y +y=1- \sqrt{10}- \sqrt{10} \)
\(\Leftrightarrow 5y=1-2 \sqrt{10}\)
\(\Leftrightarrow y=\dfrac{1-2 \sqrt{10}}{5}\)
Thay \(y=\dfrac{1-2 \sqrt{10}}{5}\) vào \((1)\), ta được:
\(x = 2\sqrt 2 .\dfrac{1-2 \sqrt{10}}{5} + \sqrt 5= \dfrac{2\sqrt 2 -4 \sqrt{20}}{5} + \sqrt 5\)
\(\Leftrightarrow x=\dfrac{2\sqrt 2 -4 .2\sqrt{5}}{5} + \sqrt 5=\dfrac{2\sqrt 2 -8\sqrt{5}+ 5\sqrt 5}{5}\)
\(\Leftrightarrow x=\dfrac{2 \sqrt 2 -3 \sqrt 5}{5}\)
Vậy hệ có nghiệm duy nhất là: \((x; y)\) = \({\left(\dfrac{2\sqrt{2} - 3\sqrt{5}}{5};\dfrac{1 - 2\sqrt{10}}{5}\right)}\)
Câu c:
Ta có:
\(\left\{ \matrix{
\left( {\sqrt 2 - 1} \right)x - y = \sqrt 2 \hfill \cr
x + \left( {\sqrt 2 + 1} \right)y = 1 \hfill \cr} \right. \)
\(\left\{ \begin{array}{l}y = \left( {\sqrt 2 - 1} \right)x - \sqrt 2 \,\,\,\,\,\left( 1 \right)\\x + \left( {\sqrt 2 + 1} \right)\left[ {\left( {\sqrt 2 - 1} \right)x - \sqrt 2 } \right] = 1\,\,\,\left( 2 \right)\end{array} \right.\)
Giải phương trình \((2)\), ta được:
\(x + \left( {\sqrt 2 + 1} \right)\left[ { \left( {\sqrt 2 - 1} \right)x} -\sqrt 2 \right] = 1\)
\(\Leftrightarrow x + (\sqrt 2 + 1) (\sqrt 2 - 1)x -( \sqrt 2 + 1). \sqrt 2 = 1\)
\(\Leftrightarrow x + {\left((\sqrt 2)^2 - 1^2 \right)}x-( 2 + \sqrt 2) = 1\)
\(\Leftrightarrow x + x = 1+( 2 + \sqrt 2)\)
\(\Leftrightarrow 2x =3 +\sqrt 2\)
\(\Leftrightarrow x=\dfrac{3+ \sqrt 2}{2}\)
Thay \(x=\dfrac{3+ \sqrt 2}{2}\) vào \((1)\), ta được:
\(y = \left( {\sqrt 2 - 1} \right).\dfrac{3+ \sqrt 2}{2} - \sqrt 2\)
\( \Leftrightarrow y= \dfrac{(\sqrt 2 - 1 )(3+ \sqrt 2)}{2} - \sqrt 2 \)
\( \Leftrightarrow y= \dfrac{3\sqrt 2 -3 +2 -\sqrt 2}{2} - \sqrt 2 \)
\( \Leftrightarrow y= \dfrac{2\sqrt 2 -1}{2} - \sqrt 2 \)
\( \Leftrightarrow y= \dfrac{2\sqrt 2 -1-2\sqrt 2}{2} \)
\( \Leftrightarrow y= \dfrac{-1}{2} \)
Vậy hệ có nghiệm \((x; y) = {\left(\dfrac{3 + \sqrt{2}}{2};\dfrac{-1}{2} \right)}\)
-- Mod Toán 9 HỌC247
-


Giải hệ phương trình sau bằng phương pháp thế: \(\left\{\begin{matrix} x - y =3 & & \\ 3x-4y=2 & & \end{matrix}\right.\)
bởi Goc pho
 18/02/2021
Theo dõi (0) 1 Trả lời
18/02/2021
Theo dõi (0) 1 Trả lời -


Cho hệ phương trình: \(\left( {IV} \right):\left\{ \begin{array}{l} 4x + y = 2\\ 8x + 2y = 1 \end{array} \right.\) Bằng minh họa hình học và phương pháp thế, chứng tỏ rằng hệ (IV) vô nghiệm.
bởi Mai Anh
 17/02/2021
Theo dõi (0) 1 Trả lời
17/02/2021
Theo dõi (0) 1 Trả lời -


Bằng minh họa hình học, hãy giải thích tại sao hệ (III) có vô số nghiệm. \(\left( {III} \right)\left\{ \matrix{4x - 2y = - 6 \hfill \cr - 2x + y = 3 \hfill \cr} \right.\)
bởi Phan Thiện Hải
 18/02/2021
Theo dõi (0) 1 Trả lời
18/02/2021
Theo dõi (0) 1 Trả lời -


Giải hệ phương trình sau bằng phương pháp thế (biểu diễn y theo x từ phương trình thứ hai của hệ) \(\left\{ \matrix{4x - 5y = 3 \hfill \cr 3x - y = 16 \hfill \cr} \right.\)
bởi Nguyễn Anh Hưng
 17/02/2021
Theo dõi (0) 1 Trả lời
17/02/2021
Theo dõi (0) 1 Trả lời -


cho hệ phương trình sau: \(\left\{ \begin{array}{l} 2{\rm{x}} - y = 1\\ x - y = 0 \end{array} \right.\) Kết quả của 2xy – 1 =?
bởi Bảo Lộc
 21/01/2021
21/01/2021
A. 0
B. 1
C. 2
D. 3
Theo dõi (0) 1 Trả lời -


Hệ phương trình sau có bao nhiêu nghiệm: \(\left\{ \begin{array}{l} {\rm{x + }}y = 5\\ {\rm{x + }}y = 3 \end{array} \right.\)
bởi Vũ Hải Yến
 21/01/2021
21/01/2021
A. Không có nghiệm
B. Có một nghiệm duy nhất.
C. Có vô số nghiệm.
D. Có hai nghiệm
Theo dõi (0) 2 Trả lời -


Hệ phương trình sau: \(\left\{ \begin{array}{l} {\rm{x + }}y = 5\\ {\rm{2x - }}y = 1 \end{array} \right.\). Tìm 2x – y =?
bởi Nguyễn Thủy Tiên
 20/01/2021
20/01/2021
A. 0
B. 1
C. 2
D. 3
Theo dõi (0) 1 Trả lời -


Cho hệ phương trình sau: \(\left\{ \begin{array}{l} {\rm{2x + }}y = 7\\ {\rm{ - x + 4}}y = 10 \end{array} \right.\). Tìm x + y = ?
bởi Lê Viết Khánh
 20/01/2021
Theo dõi (0) 1 Trả lời
20/01/2021
Theo dõi (0) 1 Trả lời -


Giải hệ phương trình sau: \(\left\{ \begin{array}{l} {\rm{2x + }}y = - 3(1)\\ {\rm{2x - }}3y = 17(2) \end{array} \right.\)
bởi Sam sung
 21/01/2021
Theo dõi (0) 1 Trả lời
21/01/2021
Theo dõi (0) 1 Trả lời -


Giải hệ phương trình sau: \(\left\{ \begin{array}{l} {\rm{4x + 5}}y = 3(1)\\ {\rm{x - }}3y = 5(2) \end{array} \right.\)
bởi Quynh Nhu
 21/01/2021
Theo dõi (0) 1 Trả lời
21/01/2021
Theo dõi (0) 1 Trả lời -


Giải hệ phương trình sau: \(\left\{ \begin{array}{l} 3{\rm{x}} - 2y = 5(1)\\ 2{\rm{x}} + y = 8(2) \end{array} \right.\)
bởi Thuy Kim
 20/01/2021
Theo dõi (0) 1 Trả lời
20/01/2021
Theo dõi (0) 1 Trả lời -


Giải hệ phương trình \(\left\{ \begin{array}{l} y - x = 5\\ \frac{{400}}{y} - \frac{{1100}}{x} = 2 \end{array} \right.\)?
bởi Trà My
 10/07/2020
10/07/2020
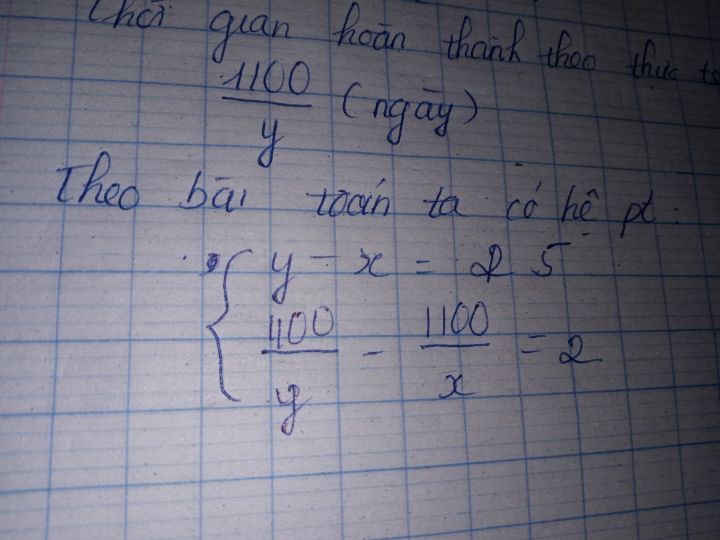 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Giải phương trình \({x^2} + 2\sqrt 2 x + 4 = 3\left( {x + \sqrt 2 } \right)\)?
bởi Quách Thị Ngọc Bích
 11/06/2020
11/06/2020
Câu b giải hộ
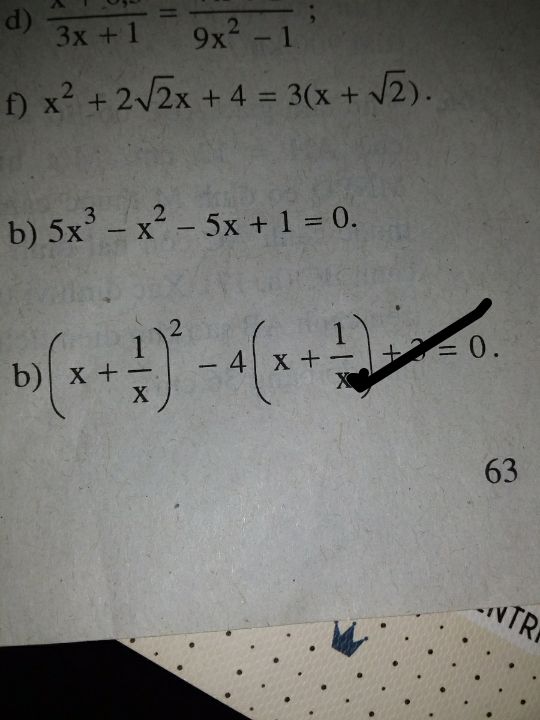 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Giải hệ phương trình \(\left\{ \begin{array}{l} x - 2y + z = 3\\ 2{x^2} - 2xy + x - 2z = - 1 \end{array} \right.\)?
bởi Lam Lam
 31/05/2020
31/05/2020
Giải bài 3 dùm mình
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 15 trang 15 SGK Toán 9 Tập 2
Bài tập 16 trang 16 SGK Toán 9 Tập 2
Bài tập 18 trang 16 SGK Toán 9 Tập 2
Bài tập 19 trang 16 SGK Toán 9 Tập 2
Bài tập 16 trang 9 SBT Toán 9 Tập 2
Bài tập 17 trang 9 SBT Toán 9 Tập 2
Bài tập 18 trang 9 SBT Toán 9 Tập 2
Bài tập 19 trang 9 SBT Toán 9 Tập 2
Bài tập 20 trang 9 SBT Toán 9 Tập 2
Bài tập 21 trang 9 SBT Toán 9 Tập 2
Bài tập 22 trang 10 SBT Toán 9 Tập 2
Bài tập 23 trang 10 SBT Toán 9 Tập 2
Bài tập 24 trang 10 SBT Toán 9 Tập 2





