Giải bài 36 tr 79 sách GK Toán 8 Tập 2
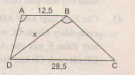
Tính độ dài x của đường thẳng BD trong hình 43 (Làm tròn đến chữ thập phân thứ nhất), biết rằng ABCD là hinh thang(AD // CD); AB= 12,5cm; CD= 28,5cm
\(\widehat {DAB} = \widehat {DBC}\)
Hướng dẫn giải chi tiết
Xét \(∆ABD\) và \(∆BDC\) có:
+) \(\widehat{DAB}\) = \(\widehat{DBC}\) (giả thiết)
+) \(\widehat{ABD}\) = \(\widehat{BDC}\) (AB//CD, hai góc so le trong)
\( \Rightarrow ∆ABD ∽ ∆BDC\) (g-g)
\( \Rightarrow \dfrac{AB}{BD} = \dfrac{BD}{DC}\) (tính chất hai tam giác đồng dạng)
\( \Rightarrow B{D^2} = AB.DC\)
\( \Rightarrow BD = \sqrt {AB.DC} = \sqrt {12,5.28,5} \) \( \approx 18,9 cm\)
-- Mod Toán 8 HỌC247
-
Nếu 2 tam giác ABC và DEF có A = 700, C = 600, E = 500, F = 700 thì chứng minh được:
bởi Hương Lan
16/01/2021
A. ΔABC ~ ΔFED
B. ΔACB ~ ΔFED
C. ΔABC ~ ΔDEF
D. ΔABC ~ ΔDFE
Theo dõi (0) 1 Trả lời -
A. 4cm
B. 8cm
C. 6cm
D. 5cm
Theo dõi (0) 1 Trả lời -
ho hình bên biết AB = 6cm, AC = 9cm, góc ABD = góc BCA. Độ dài đoạn AD là:
bởi Trần Hoàng Mai
16/01/2021
.png)
A. 2cm
B. 3cm
C. 4cm
D. 5cm
Theo dõi (0) 1 Trả lời -
Cho hai tam giác ABC và FED có A = F, cần thêm điều kiện gì dưới đây để hai tam giác (thứ tự đỉnh như vậy) đồng dạng theo trường hợp góc - góc?
bởi Aser Aser
16/01/2021
A. B = E
B. C = E
C. B = F
D. C = F
Theo dõi (0) 1 Trả lời -
Nếu 2 tam giác ABC và DEF có A = D, C = F thì:
bởi Ánh tuyết
16/01/2021
A. ΔABC ~ ΔDEF
B. ΔCAB ~ ΔDEF
C. ΔABC ~ ΔDFE
D. ΔCBA ~ ΔDFE
Theo dõi (0) 1 Trả lời -
Chọn kết luận đúng.
bởi Phạm Khánh Linh
15/01/2021
Cho tam giác ABC cân tại A, M là trung điểm của BC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho DM là tia phân giác của BDE. Chọn kết luận đúng.
A. ΔBDM ~ ΔCME
B. ΔBDM ~ ΔEMC
C. ΔBDM ~ ΔCEM
D. ΔBDM ~ ΔECM
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 35 trang 79 SGK Toán 8 Tập 2
Bài tập 37 trang 79 SGK Toán 8 Tập 2
Bài tập 38 trang 79 SGK Toán 8 Tập 2
Bài tập 39 trang 79 SGK Toán 8 Tập 2
Bài tập 40 trang 80 SGK Toán 8 Tập 2
Bài tập 41 trang 80 SGK Toán 8 Tập 2
Bài tập 42 trang 80 SGK Toán 8 Tập 2
Bài tập 43 trang 80 SGK Toán 8 Tập 2
Bài tập 44 trang 80 SGK Toán 8 Tập 2
Bài tập 45 trang 80 SGK Toán 8 Tập 2
Bài tập 39 trang 93 SBT Toán 8 Tập 2
Bài tập 40 trang 93 SBT Toán 8 Tập 2
Bài tập 41 trang 93 SBT Toán 8 Tập 2
Bài tập 42 trang 94 SBT Toán 8 Tập 2
Bài tập 43 trang 94 SBT Toán 8 Tập 2
