Giải bài 41 tr 93 sách BT Toán lớp 8 Tập 2
Hình thang ABCD (AB // CD) có AB = 2,5cm, AD = 3,5cm, BD = 5cm và \(\widehat {DAB} = \widehat {DBC}\) (h.28).
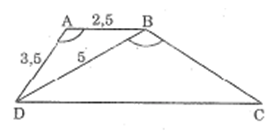
a. Chứng minh ∆ ADB đồng dạng ∆ BCD
b. Tính độ dài các cạnh BC, CD
c. Sau khi tính, hãy vẽ lại hình chính xác bằng thước và compa.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng:
Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
Từ đó suy ra các cặp cạnh tương ứng tỉ lệ và tính độ dài các đoạn thẳng.
Lời giải chi tiết
a) Vì \(AB//CD\) (gt) nên \(\widehat {ABD} = \widehat {BDC}\) (cặp góc so le trong)
Xét \(∆ ABD\) và \(∆ BDC\) có:
\(\widehat {DAB} = \widehat {DBC}\) (gt)
\(\widehat {ABD} = \widehat {BDC}\) (cmt)
\(\Rightarrow ∆ ADB\backsim ∆ BCD\) (g.g)
b) Vì \(∆ ADB\backsim ∆ BCD\) nên \(\displaystyle {{AB} \over {BD}} = {{AD} \over {BC}} = {{BD} \over {DC}}\)
Với \(AB = 2,5; AD = 3,5; BD = 5,\) ta có:
\(\eqalign{ & {{2,5} \over 5} = {{3,5} \over {BC}} = {5 \over {DC}} \cr & \Rightarrow BC = {{5.3,5} \over {2,5}} = 7\;(cm) \cr& \Rightarrow DC = {{5.5} \over {2,5}} = 10\;(cm)\cr} \)
c)
- Dựng \(\Delta ABD\) có độ dài ba cạnh \(AB=2,5cm;AD=3,5cm;\) \(BD=5cm\).
- Dựng cung tròn tâm \(B\) bán kính \(7cm\), cung tròn tâm \(D\) bán kính \(10cm\). Hai cung tròn này cắt nhau tại \(C\) (\(C\) khác phía với \(A\) so với \(BD\)).
Ta được hình thang \(ABCD\) cần dựng
-- Mod Toán 8 HỌC247
-


Tính số học sinh trong tốp quét sân của lớp 8A
bởi Tra xanh
 31/05/2019
31/05/2019
trong 1 buổi lao động lớp 8A gồm 44 hs chia thành 2 tốp. tốp 1 trồng cây và tốp 2 quét sân . tốp trồng cây đônng hơn tốp quét sân là 10 người .hỏi tốp quét sân bao nhiêu hs
Theo dõi (0) 1 Trả lời -


Giải phương trình (x+3)(x^2 + 3x - 5) - (x-3)=0
bởi Nguyễn Anh Hưng
 28/03/2019
28/03/2019
giải phương trình
a) (x+3)(x^2 + 3x - 5) - (x-3)=0
b) x-2/x+2 - 3 / x-2 = 2(x-1)/x^2 - 4Theo dõi (0) 1 Trả lời -


Chứng minh M,N,D thẳng hàng biết MM'=MA, MN=1/3 CM
bởi thủy tiên
 26/02/2019
26/02/2019
Cho tam giác ABC . M là trung điểm BC. Trên tia đối của tia MA lấy M sao cho MM'=MA. Trên CM lấy N sao MN=1/3 CM. Gọi D là trung điểm AC. Chứng minh M,N,D thẳng hàng
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác PBM đồng dạng vs tam giác MCQ
bởi Lê Minh Trí
 31/05/2019
31/05/2019
Bt1. Cho tam giác ABC đều, M là trung điểm BC. Lấy P thuộc AB và Q thuộc AC sao cho góc PMQ=\(60^0\). Chứng minh :
a)Tam giác PBM đồng dạng vs tam giác MCQ.
b)Tam giác MBP đồng dạng vs tam giác QMP.
Theo dõi (0) 1 Trả lời -


\(\Delta ABC\) có BC = 2AB, M là trung điểmn BC, D là trung điểm BM.
Chứng minh: AC = 2AD
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ABE đồng dạng tam giác ADC
bởi Anh Trần
 31/05/2019
31/05/2019
Cho tam giác ABC, kẻ tia phân giác AD. Qua B kẻ Bx sao cho ^xBC=^CAD. Tia Bx cắt AD ở E. Chứng minh:
a) ΔABE=ΔADC
b) BE2 = ED x AE
Theo dõi (0) 1 Trả lời





