Giải bài 39 tr 79 sách GK Toán 8 Tập 2
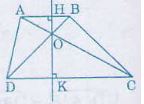
Cho hình thang ABCD(AB//CD). Gọi O là giao điểm của hai đường chéo AC và BD.
a) Chứng minh rằng OA.OD = OB.OC.
b) Đường thẳng qua O vuông góc với AB và CD theo thứ tự tại H và K.
Chứng minh rằng =
Hướng dẫn giải chi tiết
Câu a:
Vì AB // CD => ∆AOB ∽ ∆COD
⇒ =
=> OA.OD = OC.OB
Câu b:
∆AOH và ∆COK có:
=
= 900
=
⇒ ∆AOH ∽ ∆COK
⇒ =
(1)
mà =
(2)
Từ 1 và 2 => =
-- Mod Toán 8 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Bài tập 37 trang 79 SGK Toán 8 Tập 2
Bài tập 38 trang 79 SGK Toán 8 Tập 2
Bài tập 40 trang 80 SGK Toán 8 Tập 2
Bài tập 41 trang 80 SGK Toán 8 Tập 2
Bài tập 42 trang 80 SGK Toán 8 Tập 2
Bài tập 43 trang 80 SGK Toán 8 Tập 2
Bài tập 44 trang 80 SGK Toán 8 Tập 2
Bài tập 45 trang 80 SGK Toán 8 Tập 2
Bài tập 39 trang 93 SBT Toán 8 Tập 2
Bài tập 40 trang 93 SBT Toán 8 Tập 2
Bài tập 41 trang 93 SBT Toán 8 Tập 2
Bài tập 42 trang 94 SBT Toán 8 Tập 2
Bài tập 43 trang 94 SBT Toán 8 Tập 2
