Giải bài 42 tr 94 sách BT Toán lớp 8 Tập 2
Cho tam giác vuông ABC (\(\widehat A = 90^\circ \)). Dựng AD vuông góc với BC (D thuộc BC). Đường phân giác BE cắt AD tại F (h.29).
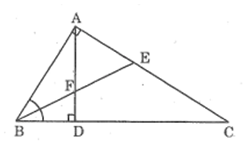
Chứng minh: \({{FD} \over {FA}} = {{EA} \over {EC}}\).
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng:
- Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
- Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy.
Lời giải chi tiết
\(\Delta ABC\) có \(BE\) là tia phân giác của góc \(ABC\) nên ta có:
\(\displaystyle {{EA} \over {EC}} = {{AB} \over {BC}}\) (tính chất đường phân giác của tam giác) (1)
\(\Delta ADB\) có \(BF\) là tia phân giác của góc \(ABD\) nên ta có:
\(\displaystyle {{FD} \over {FA}} = {{BD} \over {BA}}\) (tính chất đường phân giác của tam giác) (2)
Xét \(∆ ABC\) và \(∆ DBA\) có:
\(\widehat {BAC} = \widehat {BDA} = 90^\circ \)
\(\widehat B\) chung
\( \Rightarrow ∆ ABC \backsim ∆ DBA\) (g.g)
\( \Rightarrow\displaystyle {{BD} \over {BA}} = {{AB} \over {CB}}\) (3)
Từ (1), (2) và (3) suy ra: \(\displaystyle {{FD} \over {FA}} = {{EA} \over {EC}}\).
-- Mod Toán 8 HỌC247
-


Chứng minh BN vuông góc CM biết D, E, F là trung điểm của MB, BC, CN
bởi Trần Phương Khanh
 01/03/2019
01/03/2019
Cho tam giác ABC .Vẽ ra ngoài tam giác đó các tam giác ABM và ACN vuông cân ở A .Gọi D,E,F lần lượt là trung điểm của MB,BC,CN.Cm:
a, BN=CM
b, BN vuông góc CM
c, TAm giác DEF là tam giác cân
Theo dõi (0) 3 Trả lời -


Cho ΔABC , phân giác AD .Gọi E,F lần lượt là hình chiếu của Bvà C lên AD .
a, CM ΔABE đồng dạng với ΔACF
b, ΔBDE đồng dạng với ΔCDF
c, AE.DF= AF . DE
Theo dõi (0) 1 Trả lời -


Chứng minh 1/OE=1/OG=1/AB+1/CD biết O là giao điểm của hai đường chéo AC và BD
bởi Phạm Khánh Linh
 26/03/2019
26/03/2019
Cho hình thang ABCD (AB//CD). Gọi O là giao điểm của hai đường chéo AC và BD. Qua O kẻ đường thẳng song song với AB, cắt AD và BC theo thứ tự ở E và G.
a) Chứng minh : OA .OD = OB.OC.
b) Cho AB = 5cm, CD = 10 cm và OC = 6cm. Hãy tính OA, OE.
c) Chứng minh rằng: 1/OE=1/OG=1?AB+1/CD
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác EBD là tam giác đều
bởi Nguyễn Minh Hải
 31/05/2019
31/05/2019
Cho tam giác ABC có góc A=120 độ, phân giác AD. Trên nửa mặt phẳng bờ BC ko chứa điểm A, kẻ tia Bx tạo với BC một góc CBx=60 độ. Tia Bx cắt AD ở E. C/m:
a, AE\(\times\)BD = AB\(\times\)BE
b, Tam giác EBD là tam giác đều
c, BC\(\times\)AE = AB\(\times\)EC + AC\(\times\)BE
d, \(\dfrac{1}{AD}\) = \(\dfrac{1}{AB}\) + \(\dfrac{1}{AC}\)
Các bn giúp mk nha, chiều mai mk hok rồi. Các bn chỉ cần lm ý b thôi, mấy ý khác mk lm được rồi. Cảm ơn các bn nhiều nha.
Theo dõi (0) 1 Trả lời -


cho hình chữ nhật ABCD có AB=8cm, BC=6cm.vẽ đường cao Ah của tam giác ADB
a. chứng minh tam giác AHB đồng dạng tam giác BCD
b. chứng minh AD2=DH.DB
c.tính độ dài đoạn thẳng DH, AH
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC,D là điểm nằm trên cạnh BC sao cho DB=\(\dfrac{1}{2}\)DC.Kẻ BH và CK vuông góc với AD.Chứng minh BH= \(\dfrac{1}{2}\)CK
Theo dõi (0) 1 Trả lời







