Phần hướng dẫn giải bài tập Toán 6 Chương 1 Bài 11 Dấu hiệu chia hết cho 2, cho 5 sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các giải bài tập từ SGK Toán 6 tập 1.
-
Bài tập 123 trang 21 SBT Toán 6 Tập 1
Trong các số: 213; 435; 680; 156.
a) Số nào chia hết cho 2 mà không chia hết cho 5?
b) Số nào chia hết cho 5 mà không chia hết cho 2?
c) Số nào chia hết cho cả 2 và 5
d) Số nào không chia hết cho cả 2 và 5?
-
Bài tập 124 trang 21 SBT Toán 6 Tập 1
Tổng (hiệu) sau có chia hết cho 2 không, có chia hết cho 5 không?
a) 1.2.3.4.5 + 52
b) 1.2.3.4.5 - 75
-
Bài tập 125 trang 21 SBT Toán 6 Tập 1
Điền chữ số vào dấu * để được số 35*:
a) Chia hết cho 2
b) Chia hết cho 5
c) Chia hết cho cả 2 và 5
-
Bài tập 126 trang 22 SBT Toán 6 Tập 1
Điền chữ số thích hợp và dấu * để *45:
a) Chia hết cho 2
b) Chia hết cho 5
-
Bài tập 127 trang 22 SBT Toán 6 Tập 1
Dùng ba chữ số 6,0,5 hãy ghép thành các số tự nhiên có ba chữ số thoả mãn một trong các điều kiện:
a) Số đó chia hết cho 2
b) Số đó chia hết cho 5
-
Bài tập 128 trang 22 SBT Toán 6 Tập 1
Tìm số tự nhiên có hai chữ số, các chữ số giông nhau, biết rằng số đó chia hết cho 2, còn chia hết cho 5 dư 4.
-
Bài tập 129 trang 22 SBT Toán 6 Tập 1
Dùng cả ba chữ số 3,4,5 hãy ghép thành các số tự nhiên có 3 chữ số:
a) Lớn nhất và chia hết cho 2
b) Nhỏ nhất và chia hết cho 5
-
Bài tập 130 trang 22 SBT Toán 6 Tập 1
Tìm tập hợp các số tự nhiên n vừa chia hết cho 2 vừa chia hết cho 5 và 136 < n < 182
-
Bài tập 131 trang 22 SBT Toán 6 Tập 1
Từ 1 đến 100 có bao nhiêu số chia hết cho 2, có bao nhiêu số chia hết cho 5?
-
Bài tập 132 trang 22 SBT Toán 6 Tập 1
Chứng tỏ rằng với mọi số tự nhiên n thì tích (n + 3)(n +6) chia hết cho 2.
-
Bài tập 11.1 trang 22 SBT Toán 6 Tập 1
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
a) Số có chữ số tận cùng là 8 thì chia hết cho 2;
b) Số chia hết cho 2 thì có chữ số tận cùng là 8;
c) Số chia hết cho 5 thì có chữ số tận cùng bằng 0;
b) Số có chữ số tận cùng bằng 0 thì chia hết cho 5 và chia hết cho 2.
-
Bài tập 11.2 trang 22 SBT Toán 6 Tập 1
Có bao nhiêu số tự nhiên nhỏ hơn 100 chia cho 5 dư 3?
-
Bài tập 11.3 trang 22 SBT Toán 6 Tập 1
Chứng tỏ rằng với mọi số tự nhiên n thì tích n.(n + 5) chia hết cho 2.
-
Bài tập 11.4 trang 22 SBT Toán 6 Tập 1
Gọi A = n2 + n + 1 (n ∈ N). Chứng tỏ rằng:
a) A không chia hết cho 2.
b) A không chia hết cho 5.
-
Bài tập 91 trang 38 SGK Toán 6 Tập 1
Trong các số sau, số nào chia hết cho 2, số nào chia hết cho 5 ?
652; 850; 1546; 785; 6321.
-
Bài tập 92 trang 38 SGK Toán 6 Tập 1
Cho các số 2141; 1345; 4620; 234. Trong các số đó:
a) Số nào chia hết cho 2 mà không chia hết cho 5?
b) Số nào chia hết cho 5 mà không chia hết cho 2?
c) Số nào chia hết cho cả 2 và 5?
-
Bài tập 93 trang 38 SGK Toán 6 Tập 1
Tổng (hiệu) sau có chia hết cho 2 không, có chia hết cho 5 không ?
a) 136 + 420; b) 625 - 450;
c) 1 . 2 . 3 . 4 . 5 . 6 + 42; d) 1 . 2 . 3 . 4 . 5 . 6 - 35.
-
Bài tập 94 trang 38 SGK Toán 6 Tập 1
Không thực hiện phép chia, hãy tìm số dư khi chia mỗi số sau đây cho 2, cho 5:
813; 264; 736; 6547.
-
Bài tập 95 trang 38 SGK Toán 6 Tập 1
Điền chữ số vào dấu * để được số
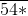 thỏa mãn điều kiện:
thỏa mãn điều kiện:a) Chia hết cho 2; b) Chia hết cho 5.
-
Bài tập 96 trang 39 SGK Toán 6 Tập 1
Điền chữ số vào dấu * để được \(\overline{*85}\) thỏa mãn điều kiện:
a) Chia hết cho 2; b) Chia hết cho 5.
-
Bài tập 97 trang 39 SGK Toán 6 Tập 1
Dùng ba chữ số 4, 0, 5, hãy ghép thành các số tự nhiên có ba chữ số khác nhau thỏa mãn điều kiện:
a) Số đó chia hết cho 2; b) Số đó chia hết cho 5.
-
Bài tập 98 trang 39 SGK Toán 6 Tập 1
Đánh dấu "X" vào ô thích hợp trong các câu sau:
Câu
Đúng
Sai
a) Số có chữ số tận cùng bằng 4 thì chia hết cho 2.
b) Số chia hết cho 2 thì có chữ số tận cùng bằng 4.
c) Số chia hết cho 2 và chia hết cho 5 thì có chữ số tận cùng bằng 0.
d) Số chia hết cho 5 thì có chữ số tận cùng bằng 5.
-
Bài tập 99 trang 39 SGK Toán 6 Tập 1
Tìm số tự nhiên có hai chữ số, các chữ số giống nhau, biết rằng số đó chia hết cho 2 và chia cho 5 thì dư 3.
-
Bài tập 100 trang 39 SGK Toán 6 Tập 1
Ô tô đầu tiên ra đời năm nào ?
Ô tô đầu tiên ra đời năm \( n=\overline{abcd}\), trong đó n \(\vdots\) 5 và a, b, c \(\in\) {1; 5; 8} (a, b, c khác nhau).






