Bài tập 16 trang 28 SGK Toán 11 NC
Tìm nghiệm của các phương trình sau trong khoảng đã cho
a. \(\sin 2x = - \frac{1}{2}\) với 0 < x < π
b. \(\cos \left( {x - 5} \right) = \frac{{\sqrt 3 }}{2}\) với −π < x < π
Hướng dẫn giải chi tiết
a)
\(\begin{array}{l}
\sin 2x = - \frac{1}{2} \Leftrightarrow \sin 2x = \sin \left( { - \frac{\pi }{6}} \right)\\
\Leftrightarrow \left[ \begin{array}{l}
2x = - \frac{\pi }{6} + k2\pi \\
2x = \frac{{7\pi }}{6} + k2\pi
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x = - \frac{\pi }{{12}} + k\pi \\
x = \frac{{7\pi }}{{12}} + k\pi
\end{array} \right.\left( {k \in Z} \right)
\end{array}\)
Với điều kiện 0 < x < π ta có:
\(\begin{array}{l}
0 < - \frac{\pi }{{12}} + k\pi < \pi \\
\Leftrightarrow \frac{1}{{12}} < k < \frac{{13}}{{12}},k \in Z
\end{array}\)
Nên k = 1, khi đó ta có nghiệm \(x = \frac{{11\pi }}{{12}}\)
\(\begin{array}{l}
0 < \frac{{7\pi }}{{12}} + k\pi < \pi \\
\Leftrightarrow - \frac{7}{{12}} < k < \frac{5}{{12}},k \in Z
\end{array}\)
Nên k = 0, khi đó ta có nghiệm \(x = \frac{{7\pi }}{{12}}\)
Vậy phương trình đã cho có hai nghiệm trong khoảng (0;π) là:
\(x = \frac{{7\pi }}{{12}}\) và \(x = \frac{{11\pi }}{{12}}\)
b)
\(\begin{array}{l}
\cos \left( {x - 5} \right) = \frac{{\sqrt 3 }}{2} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x - 5 = \frac{\pi }{6} + k2\pi }\\
{x - 5 = - \frac{\pi }{6} + k2\pi }
\end{array}} \right.\\
\Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \frac{\pi }{6} + 5 + k2\pi }\\
{x = - \frac{\pi }{6} + 5 + k2\pi }
\end{array}} \right.
\end{array}\)
Ta tìm k để điều kiện – π< x < π được thỏa mãn.
Xét họ nghiệm thứ nhất:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
- \pi < \frac{\pi }{6} + 5 + k2\pi \\
\Leftrightarrow - 7\pi - 30 < 12k\pi < 5\pi - 30
\end{array}\\
{ \Leftrightarrow - \frac{7}{{12}} - \frac{{30}}{{12\pi }} < k < \frac{5}{{12}} - \frac{{30}}{{12\pi }}}
\end{array}\)
Vì \( - 1,38 < - \frac{7}{{12}} - \frac{{30}}{{12\pi }} < k < \frac{5}{{12}} - \frac{{30}}{{12\pi}},k \in Z \) nên \( - 1,38 < k < - 0,37\)
Chỉ có một giá trị k nguyên thỏa mãn các điều kiện đó là k = - 1.
Ta có nghiệm thứ nhất của phương trình là \(x = \frac{\pi }{6} + 5 - 2\pi = 5 - \frac{{11\pi }}{6}\)
Tương tự, xét họ nghiệm thứ hai:
\(\begin{array}{l}
- \pi < - \frac{\pi }{6} + 5 + k2\pi < \pi \\
\Leftrightarrow - 5\pi - 30 < 12k\pi < 7\pi - 30
\end{array}\)
Vậy k = −1
Ta có nghiệm thứ hai của phương trình là \(x = - \frac{\pi }{6} + 5 - 2\pi = 5 - \frac{{13\pi }}{6}\)
Vậy \(x = 5 - \frac{{11\pi }}{6},x = 5 - \frac{{13\pi }}{6}\)
-- Mod Toán 11 HỌC247
-


Giải phương trình \(\sin (3x+ {p \over 3})={1 \over 4}\)?
bởi Huy
 31/08/2020
Theo dõi (0) 0 Trả lời
31/08/2020
Theo dõi (0) 0 Trả lời -


Giải phương trình \(\sin ^2- 2\cos x+ 2 =0\)?
bởi Thỏ Cony
 27/08/2020
27/08/2020
Phần tự luận
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


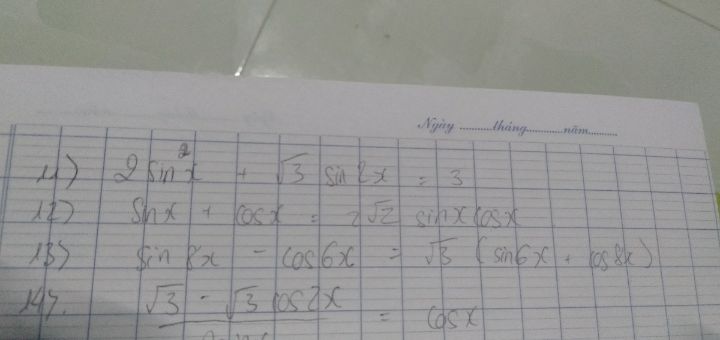
Giải phương trình \(2\sin ^2x + √3.\sin 2x = 3\)?
bởi Hồng Hạnh
 26/08/2020
26/08/2020
Giải hộ mình với ạ
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Giải phương trình \(\sin ^2 x =\dfrac{1}{2}\)?
bởi Thuyền Việt
 18/08/2020
18/08/2020
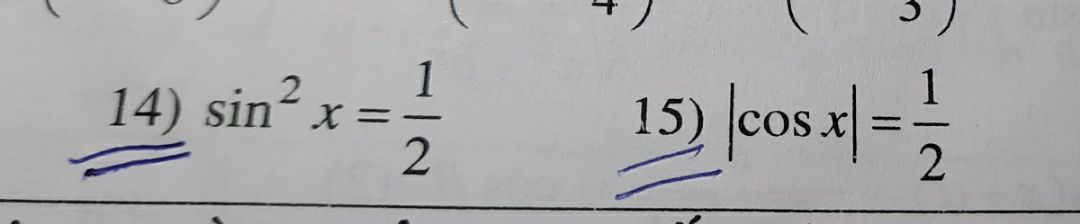 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải phương trình \(4{\sin ^4}\frac{x}{2} + 4{\cos ^2}\frac{x}{2} = \sqrt 3 \sin x\cos x + 1\)?
bởi Nguyễn Minh
 15/08/2020
Theo dõi (0) 0 Trả lời
15/08/2020
Theo dõi (0) 0 Trả lời -


Giải phương trình \({\rm{cos}}\left( {2x - \frac{\pi }{3}} \right) = \frac{{\sqrt 3 }}{2}\)?
bởi Phạm Thơm
 15/08/2020
15/08/2020
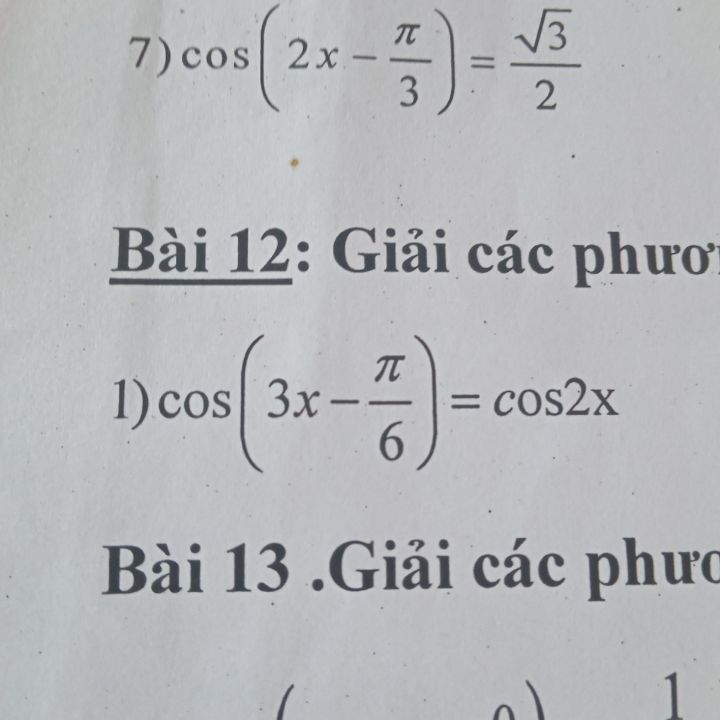 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Giải phương trình \(5\sin 5x=-\sin \sqrt 3\)?
bởi Trần Hùng Sơn
 14/08/2020
14/08/2020
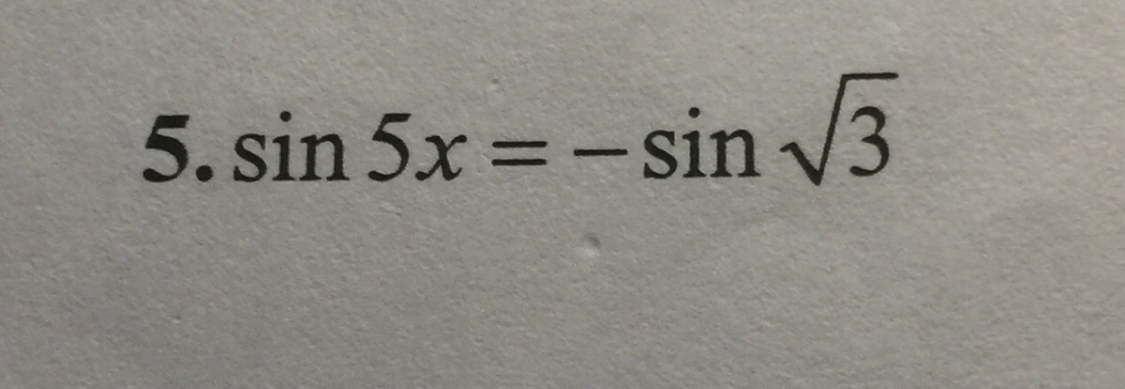 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 14 trang 28 SGK Toán 11 NC
Bài tập 15 trang 28 SGK Toán 11 NC
Bài tập 17 trang 29 SGK Toán 11 NC
Bài tập 18 trang 29 SGK Toán 11 NC
Bài tập 19 trang 29 SGK Toán 11 NC
Bài tập 20 trang 29 SGK Toán 11 NC
Bài tập 21 trang 29 SGK Toán 11 NC
Bài tập 22 trang 30 SGK Toán 11 NC
Bài tập 23 trang 31 SGK Toán 11 NC
Bài tập 24 trang 32 SGK Toán 11 NC





