Bài tập 21 trang 29 SGK Toán 11 NC
Khi giải phương trình \(\tan x = \sqrt 3 \); bạn Phương nhận thấy \( - \sqrt 3 = \tan \left( { - \frac{\pi }{3}} \right)\) và viết \(\tan x = - \sqrt 3 \Leftrightarrow \tan x = \tan \left( { - \frac{\pi }{3}} \right) \Leftrightarrow x = - \frac{\pi }{3} + k\pi \).
Cũng phương trình đó, bạn Quyên lấy \( - \sqrt 3 = \tan \frac{{2\pi }}{3}\) nên giải như sau:
\(\begin{array}{l}
\tan x = - \sqrt 3 \Leftrightarrow \tan x = \tan \frac{{2\pi }}{3}\\
\Leftrightarrow x = \frac{{2\pi }}{3} + k\pi
\end{array}\)
Theo em, ai giải đúng, ai giải sai ?
Hướng dẫn giải chi tiết
Cả hai bạn đều giải đúng. Hai họ nghiệm chỉ khác nhau về hình thức, thực chất chỉ là một.
Thực vậy, họ nghiệm \(x = \frac{{2\pi }}{3} + k\pi \) có thể viết lại là \(x = \frac{{2\pi }}{3} - \pi + \left( {k + 1} \right)\pi \) hay \( - \frac{\pi }{3} + \left( {k + 1} \right)\pi \); đây chính là kết quả mà phương tìm được.
-- Mod Toán 11 HỌC247
-


Giải phương trình 2cos3x+căn 3 sinx=2cos^2(x/2)-1
bởi Tra Vu Huong
 20/07/2019
20/07/2019
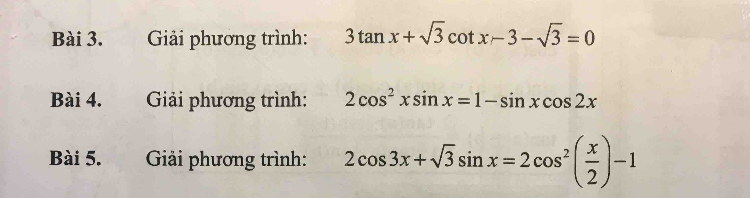 Theo dõi (3) 7 Trả lời
Theo dõi (3) 7 Trả lời -


Giải pt (sin^4x+cos^4x)/sinx=1/4
bởi Lê Thị Hường
 08/07/2019
08/07/2019
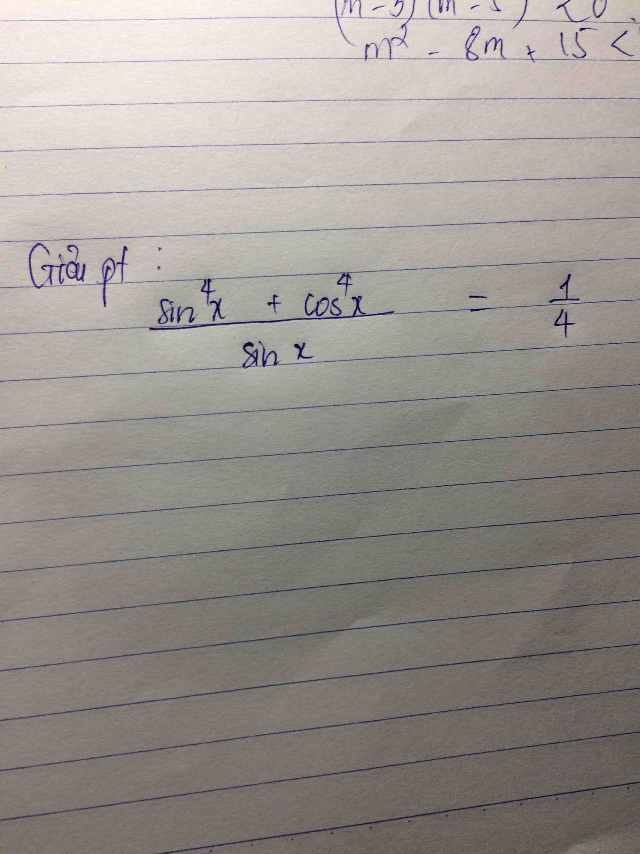 Theo dõi (1) 7 Trả lời
Theo dõi (1) 7 Trả lời -


Giải pt sinx= cos 2x
bởi Lê Thị Hường
 05/07/2019
Giải pt: sinx= cos 2xTheo dõi (0) 3 Trả lời
05/07/2019
Giải pt: sinx= cos 2xTheo dõi (0) 3 Trả lời -


Giải phương trình sin3x-4sinxcos2x=0Cos2x/sinx=0
bởi Ngọc Điền
 25/06/2019
Sin3x-4sinxcos2x=0Cos2x/sinx=0Theo dõi (1) 5 Trả lời
25/06/2019
Sin3x-4sinxcos2x=0Cos2x/sinx=0Theo dõi (1) 5 Trả lời -


Chứng minh sinx.cot2a=cos3x
bởi Quang Phan
 25/10/2018
25/10/2018
sinx nhân cot2x bằng cos3x
Theo dõi (0) 0 Trả lời -


Tìm tập xác định của hàm số y=2tanx-cotx-3
bởi tran quoc truong
 21/09/2018
21/09/2018
TXĐ hàm số y=2tanx-cotx-3
Theo dõi (0) 2 Trả lời -


Giải phương trinh tan3x.tanx=1
bởi Nguyễn Hường
 20/09/2018
20/09/2018
tan3x.tanx=1
Theo dõi (0) 2 Trả lời -


Giải phuong trình sin3x - cos2x=0
bởi Nguyễn Hường
 18/09/2018
18/09/2018
sin3x - cos2x=0
Theo dõi (0) 2 Trả lời -


Cho 0 < x < π/2 , Sinx + √2.Sin( π/2 -x) = √ 2
Tính tan(x + pi/4)
giúp tớ gấp
Theo dõi (0) 1 Trả lời






