Bài tập 24 trang 32 SGK Toán 11 NC
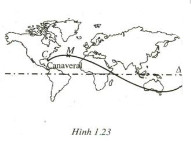
Giả sử một con tàu vũ trụ được phóng lên từ mũi Ca-na-vơ-ran (Canaveral) ở Mĩ. Nó chuyển động theo một quỹ đạo được mô tả trên một bản đồ phẳng (quanh đường xích đạo) của mặt đất
như hình 1.23: điểm M mô tả cho con tàu, đường thẳng Δ mô tả cho đường xích đạo.
Khoảng cách h (kilomet) từ M đến Δ được tính theo công thức h = |d|, trong đó:
\(d = 400\cos \left[ {\frac{\pi }{{45}}\left( {t - 10} \right)} \right]\)
Với t (phút) là thời gian trôi qua kể từ khi con tàu đi vào quỹ đạo, d > 0 nếu M ở phía trên Δ, d < 0 nếu M ở phía dưới Δ.
a. Giả thiết rằng con tàu đi vào quỹ đạo ngay từ khi phóng lên tại mũi Ca-na-vơ-ran (tức là ứng với t = 0). Hãy tính khoảng cách từ điểm C đến đường thẳng Δ, trong đó C là điểm trên bản đồ biểu diễn cho mũi Ca-na-vơ-ran.
b. Tìm thời điểm sớm nhất sau khi con tàu đi vào quỹ đạo để có d = 2000.
c. Tìm thời điểm sớm nhất sau khi con tàu đi vào quỹ đạo để có d = −1236.
(Tính chính xác các kết quả đến hàng phần nghìn).
Hướng dẫn giải chi tiết
a) Vì t = 0 nên \(d = 4000\cos \left( { - \frac{{10\pi }}{{45}}} \right) = 400\cos \frac{{2\pi }}{9}\). Do đó:
\(h = \left| d \right| \approx 3064,178\left( {km} \right)\)
b)
\(\begin{array}{*{20}{l}}
\begin{array}{l}
d = 2000 \Leftrightarrow 400\cos \left[ {\frac{\pi }{{45}}\left( {t - 10} \right)} \right] = 2000\\
\Leftrightarrow \cos \left[ {\frac{\pi }{{45}}\left( {t - 10} \right)} \right] = \frac{1}{2}
\end{array}\\
{ \Leftrightarrow \frac{\pi }{{45}}\left( {t - 10} \right) = \pm \frac{\pi }{3} + k2\pi }\\
{ \Leftrightarrow t = 10 \pm 15 + 90k}\\
{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{t = 25 + 90k}\\
{t = - 5 + 90k}
\end{array}} \right.}
\end{array}\)
Chú ý rằng t > 0 ta thấy ngay giá trị nhỏ nhất của t là t = 25. Vậy d = 2000 (km) xảy ra lần đầu tiên sau khi phóng con tàu vào quỹ đạo được 25 phút.
c)
\(\begin{array}{*{20}{l}}
\begin{array}{l}
d = - 1236 \Leftrightarrow 400\cos \left[ {\frac{\pi }{{45}}\left( {t - 10} \right)} \right] = - 1236\\
\Leftrightarrow \cos \left[ {\frac{\pi }{{45}}\left( {t - 10} \right)} \right] = - 0,309
\end{array}\\
{ \Leftrightarrow \frac{\pi }{{45}}\left( {t - 10} \right) = \pm \alpha + k2\pi \left( {k \in Z,cos\alpha = - 0,309} \right)}\\
{ \Leftrightarrow t = \pm \frac{{45}}{\pi }\alpha + 10 + 90k}
\end{array}\)
Sử dụng bảng số hoặc máy tính bỏ túi, ta có thể chọn \(\alpha \approx 1,885\). Khi đó ta có:
\(t \approx \pm 27,000 + 10 + 90k\), tức là \(t \approx - 17,000 + 90k\) hoặc \(t \approx 37,000 + 90k\)
Dễ thấy giá trị dương nhỏ nhất của tt là 37,000. Vậy d = −1236 (km) xảy ra lần đầu tiên là 37,000 phút sau khi con tàu được phóng vào quỹ đạo.
-- Mod Toán 11 HỌC247
-


Rút gọn biểu thức A=(tan2a - sin2a)/(cot2a - cos2a)
bởi Thuy Kim
 25/09/2018
25/09/2018
rút gọn biểu thức A = (tan2a - sin2a) / (cot2a - cos2a) là bao nhiêu ?
Theo dõi (0) 1 Trả lời -


Bài 2.3 trang 23 sách bài tập Toán 11
bởi Anh Trần
 25/09/2018
Bài 2.3 (SBT trang 23)
25/09/2018
Bài 2.3 (SBT trang 23)Giải các phương trình :
a) \(\tan\left(2x+45^0\right)=-1\)
b) \(\cot\left(x+\dfrac{\pi}{3}\right)=\sqrt{3}\)
c) \(\tan\left(\dfrac{x}{2}-\dfrac{\pi}{4}\right)=\tan\dfrac{\pi}{8}\)
d) \(\cot\left(\dfrac{x}{3}+20^0\right)=-\dfrac{\sqrt{3}}{3}\)
Theo dõi (0) 1 Trả lời -


Giải phương trình 3cot(x-pi/3)=căn 3
bởi A La
 25/09/2018
25/09/2018
3cot(x-\(\pi\)/3) = \(\sqrt{3}\)
Theo dõi (0) 1 Trả lời -


Tìm GTLN của y=cos2x−sinx
bởi Sam sung
 25/09/2018
25/09/2018
giá trị lớn nhất của biểu thức y=cos2x−sinx là bao nhiêu ?
Theo dõi (0) 1 Trả lời -


Chứng minh phương trình sinx-2cosx=3 vô nghiệm
bởi Lê Tấn Thanh
 25/09/2018
25/09/2018
chứng minh rằng các phương trình sau đây vô nghiệm : a) \(\sin x-2\cos x=3\) ; b) \(5\sin2x+\sin x+\cos x+6=0\)
Theo dõi (0) 1 Trả lời -


Giải phương trình sin4x=sin pi/5
bởi minh dương
 25/09/2018
25/09/2018
giải các phương trình sau : a) \(\sin4x=\sin\frac{\pi}{5}\) ; b) \(\sin\left(\frac{x+\pi}{5}\right)=-\frac{1}{2}\) ; c) \(\cos\frac{x}{2}=\cos\sqrt{2}\) ; d) \(\cos\left(x+\frac{\pi}{18}\right)=\frac{2}{5}\)
Theo dõi (0) 1 Trả lời -


Giải phương trình cot3x=tan(2pi/5)
bởi Phạm Khánh Linh
 25/09/2018
25/09/2018
giải các phương trình sau : a) \(\tan3x=\tan\frac{3\pi}{5}\) ; b) \(\tan\left(x-15^o\right)=5\) ; c) \(\tan\left(2x-1\right)=\sqrt{3}\) ; d) \(\cot2x=\cot\left(-\frac{1}{3}\right)\) ; e) \(\cot\left(\frac{x}{4}+20^o\right)=-\sqrt{3}\) ; f) \(\cot3x=\tan\frac{2\pi}{5}\)
Theo dõi (0) 1 Trả lời -


Giải phương trình cos^2 x.cos2x=0
bởi Anh Nguyễn
 25/09/2018
25/09/2018
giải phương trình sau : \(\cos^2x\cos2x=0\)
Theo dõi (0) 2 Trả lời -


tìm nghiệm của các phương trình sau trên khoảng đã cho : a) \(\tan\left(2x-15^o\right)=1\) với \(-180^o\le x\le90^o\) ; b) \(\cot3x=-\frac{1}{\sqrt{3}}\) với \(-\frac{\pi}{2}\le x\le0\)
Theo dõi (1) 1 Trả lời





