-
Câu hỏi:
Cho đường tròn \(\left( O;R \right)\) ngoại tiếp lục giác đều ABCDEF. Khi đó số đo cung của đường tròn có độ dài bằng chu vi lục giác theo độ và rad lần lượt là:
- A. \(360{}^\circ \) và \(2\pi \)
- B. \(360{}^\circ \) và \(\pi \)
- C. \(\frac{1080{}^\circ }{\pi }\) và 6
- D. \(1080{}^\circ \) và \(6\pi \)
Lời giải tham khảo:
Đáp án đúng: C
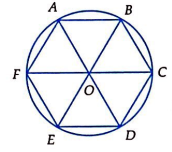
ABCDEF là lục giác đều \(\Rightarrow \widehat{AOB}=\frac{360{}^\circ }{6}=60{}^\circ \)
\(OA=OB\Rightarrow \Delta AOB\) đều \(\Rightarrow AB=OA=R\Rightarrow \) Chu vi ABCDEF là \(6R\)
\(\Rightarrow \) Cung có độ dài \(6R\) có số đo 6 rad
6 rad \(=6.\frac{180{}^\circ }{\pi }=\frac{1080{}^\circ }{\pi }\)
Đáp án C.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Một đường tròn có bán kính \(R=10cm\). Tìm số đo (rad) của cung có độ dài là 5cm.
- Cho đường tròn \(\left( O;R \right)\) ngoại tiếp lục giác đều ABCDEF.
- Trong mặt phẳng tọa độ Oxy, cho đường tròn lượng giác. M thuộc đường tròn sao cho \(\widehat{AOM}=\frac{\pi }{6}\)
- Cho bốn cung (trên một đường tròn định hướng): \(\alpha =\frac{\pi }{3};\beta =\frac{10\pi }{3}\);
- Đổi số đo cung sau sang radian: \(70{}^\circ \) (làm tròn đến hàng phần nghìn).
- Đổi số đo cung sau sang độ, phút, giây: \(\frac{5}{6}\text{rad}\).
- Trên đường tròn lượng giác, cho cung lượng giác \(s\overset{\curvearrowright }{\mathop{AM}}\,\)
- Chọn điểm \(A\left( 1;0 \right)\) làm điểm đầu cung lượng giác trên đường tròn lượng giác.
- Một đường tròn bán kính 20cm. Tính độ dài cung trên đường tròn có số đo \(\frac{\pi }{16}\)
- Khi biểu diễn cung lượng giác trên đường tròn trên lượng giác. Khẳng định nào dưới đây là sai?







