Hoạt động khám phá 2 trang 9 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
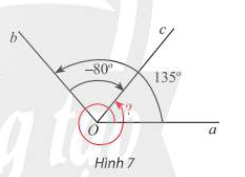
Cho Hình 7.
a) Xác định số đo các góc lượng giác (Oa,Ob), (Ob,Oc) và (Oa,Oc).
b) Nhận xét về mối liên hệ giữa ba số đo góc này.
Hướng dẫn giải chi tiết Hoạt động khám phá 2
Phương pháp giải:
- Quy ước chiều quay ngược chiều kim đồng hồ là chiều dương và chiều quay cùng chiều kim đồng hồ là chiều âm.
Lời giải chi tiết:
a) Số đo của góc lượng giác (Oa,Ob) trong Hình 7 là \({135^ \circ } + n{.360^ \circ },(n \in \mathbb{Z})\)
Số đo của góc lượng giác (Ob,Oc) trong Hình 7 là \( - {80^ \circ } + m{.360^ \circ },(m \in \mathbb{Z})\)
Số đo của góc lượng giác (Oa,Oc) trong Hình 7 là \({415^ \circ } + k{.360^ \circ },(k \in \mathbb{Z})\)
b)
\(\begin{array}{l}(Oa,Ob) + (Ob,Oc) = {135^ \circ } + n{.360^ \circ } + ( - {80^ \circ }) + m{.360^ \circ }\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {55^ \circ } + (n + m){.360^ \circ } = {415^ \circ } + (n + m - 1){.360^ \circ }\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {415^ \circ } + k{.360^ \circ } = (Oa,Oc)\end{array}\)
với \(k = n + m - 1\,;n,m,k \in \mathbb{Z}\)
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Thực hành 1 trang 9 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Vận dụng 1 trang 9 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Vận dụng 2 trang 9 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 3 trang 10 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 2 trang 11 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 4 trang 11 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 3 trang 12 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 1 trang 12 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 2 trang 12 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 3 trang 12 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 4 trang 12 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 5 trang 12 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 6 trang 12 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 7 trang 13 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 8 trang 13 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 9 trang 13 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Bài tập 1 trang 8 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 2 trang 8 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 3 trang 8 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 4 trang 9 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 5 trang 9 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 6 trang 9 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 7 trang 9 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 8 trang 9 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 9 trang 9 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 10 trang 9 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 11 trang 10 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 12 trang 10 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 13 trang 10 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST