Giải bài 18 trang 75 SGK Toán 10 Chân trời sáng tạo tập 2
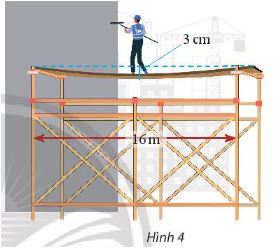
Một người đứng giữa một tấm ván gỗ đặt trên một giàn giáo để sơn tường nhà. Biết rằng dàn giáo dài 16m và độ võng tại tâm của ván gỗ (điểm ở giữa của ván gỗ) là 3 cm (hình 4). Cho biết đường cong của ván gỗ có hình parabol
a) Giả sử tâm ván gỗ trùng với đỉnh của parabol, tìm phương trình chính tắc của parabol
b) Điểm có độ võng 1 cm cách tâm ván gỗ bao xa?
Hướng dẫn giải chi tiết Bài 18
Phương pháp giải
a) Bước 1: Giả sử phương trình chính tắc của parabol có dạng \({y^2} = 2px\)
Bước 2: Từ giả thiết, xác định điểm thuộc parabol
Bước 3: Thay tọa độ điểm đó vào phương trình \({y^2} = 2px\), tìm p và xác định phương trình chính tắc của parabol
b) Thay \(x = 1\) vào phương trình chính tắc vừa tìm được tìm y
Lời giải chi tiết
a) Ta vẽ lại parabol và chọn hệ trục tọa độ như hình dưới
Giả sử phương trình chính tắc của parabol có dạng \({y^2} = 2px\)
Từ giả thiết ta có: \(AB = 2{y_A} = 16 \Rightarrow {y_A} = 8 \Rightarrow A\left( {0,03;8} \right)\)
Thay tọa độ điểm A vào phương trình \({y^2} = 2px\)ta được \({8^2} = 2p.0,03 \Rightarrow p = \frac{{3200}}{3}\)
Vậy Phương trình chính tắc của parabol có dạng \({y^2} = \frac{{6400}}{3}x\)
b) Thay \(x = 1\)vào phương trình \({y^2} = \frac{{6400}}{3}x\) ta có \({y^2} = \frac{{6400}}{3}.1 \Rightarrow y = \frac{{80\sqrt 3 }}{3} \simeq 46,2\)
Vậy điểm có độ võng 1 cm cách tâm ván gỗ gần bằng 46,2 m
Chú ý khi giải: đổi về cùng đơn vị đo
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải bài 16 trang 75 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 17 trang 75 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 1 trang 77 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 2 trang 77 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 3 trang 77 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 4 trang 77 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 5 trang 77 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 6 trang 77 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 7 trang 77 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 8 trang 78 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 9 trang 78 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 10 trang 78 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 11 trang 78 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 12 trang 78 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 1 trang 78 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 2 trang 78 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 3 trang 79 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 4 trang 79 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 5 trang 79 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 6 trang 79 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 7 trang 79 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 8 trang 79 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 9 trang 79 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 10 trang 79 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 11 trang 80 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 12 trang 80 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 13 trang 80 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 14 trang 80 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 15 trang 80 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 16 trang 80 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 17 trang 80 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 18 trang 80 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 19 trang 80 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST