Giải Bài 18 trang 80 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST

Phương pháp giải

Parabol \(\left( P \right)\) có dạng \({y^2} = 2px\) với \(p > 0\) có tiêu điểm \(F\left( {\frac{p}{2};0} \right)\), phương trình đường chuẩn \(\Delta :x =  - \frac{p}{2}\)

Lời giải chi tiết

Gọi phương trình \(\left( P \right)\) có dạng \({y^2} = 2px\)

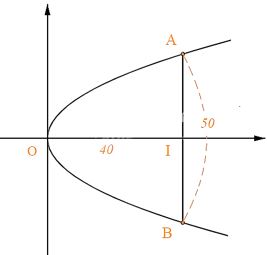
Khi đó gương là phần mặt phẳng tạo bởi đường cong AOB.

Ta có: Chiều rộng giữa hai mép gương là 50 cm, suy ra AB = 50cm.

Chiều sâu của gương là 40 cm suy ra OI = 40 cm.

Do đó AI = 50: 2= 25 và A(40; 25) thuộc vào parabol (P)

Thay điểm \(A\left( {40;25} \right)\) vào phương trình ta có \(p = \frac{{{y^2}}}{{2x}} = \frac{{{{25}^2}}}{{2.40}} \approx 7,8\)

\( \Rightarrow \left( P \right):{y^2} = 15,6x\)

-- Mod Toán 10 HỌC247