HŲ░ß╗øng dß║½n Giß║Żi b├Āi tß║Łp To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo ChŲ░ŲĪng 9 B├Āi 3 ─ÉŲ░ß╗Øng tr├▓n trong mß║Ęt phß║│ng tß╗Źa ─æß╗Ö gi├║p c├Īc em hß╗Źc sinh nß║»m vß╗»ng phŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp v├Ā ├┤n luyß╗ćn tß╗æt kiß║┐n thß╗®c.
-
Hoß║Īt ─æß╗Öng kh├Īm ph├Ī 1 trang 59 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
H├Ży nhß║»c lß║Īi c├┤ng thß╗®c t├Łnh khoß║Żng c├Īch giß╗»a 2 ─æiß╗ām \(I\left( {a;b} \right)\) v├Ā \(M\left( {x;y} \right)\)trong mß║Ęt phß║│ng Oxy
-
Thß╗▒c h├Ānh 1 trang 60 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Viß║┐t phŲ░ŲĪng tr├¼nh ─æŲ░ß╗Øng tr├▓n (C) trong c├Īc trŲ░ß╗Øng hß╗Żp sau:
a) (C) c├│ t├óm \(O\left( {0;0} \right)\), b├Īn k├Łnh \(R = 4\)
b) (C) c├│ t├óm \(I\left( {2; - 2} \right)\), b├Īn k├Łnh \(R = 8\)
c) (C) ─æi qua 3 ─æiß╗ām \(A(1;4), B(0;1), C(4;3)\)
-
Thß╗▒c h├Ānh 2 trang 61 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
PhŲ░ŲĪng tr├¼nh n├Āo trong c├Īc phŲ░ŲĪng tr├¼nh sau ─æ├óy l├Ā phŲ░ŲĪng tr├¼nh ─æŲ░ß╗Øng tr├▓n? T├¼m tß╗Źa ─æß╗Ö t├óm v├Ā b├Īn k├Łnh cß╗¦a ─æŲ░ß╗Øng tr├▓n ─æ├│
a) \({x^2} + {y^2} - 2x - 4y - 20 = 0\)
b) \({\left( {x + 5} \right)^2} + {\left( {y + 1} \right)^2} = 121\)
c) \({x^2} + {y^2} - 4x - 8y + 5 = 0\)
d) \(2{x^2} + 2{y^2} + 6x + 8y - 2 = 0\)
-
Vß║Łn dß╗źng 1 trang 61 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Theo dß╗» kiß╗ćn ─æ├Ż cho trong hoß║Īt ─æß╗Öng khß╗¤i ─æß╗Öng cß╗¦a b├Āi hß╗Źc, viß║┐t phŲ░ŲĪng tr├¼nh ─æŲ░ß╗Øng tr├▓n biß╗āu diß╗ģn tß║Łp hß╗Żp c├Īc ─æiß╗ām xa nhß║źt m├Ā v├▓i nŲ░ß╗øc c├│ thß╗ā phun tß╗øi
-
Vß║Łn dß╗źng 2 trang 61 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Mß╗Öt s├ón khß║źu ─æ├Ż ─æŲ░ß╗Żc thiß║┐t lß║Łp mß╗Öt hß╗ć trß╗źc tß╗Źa ─æß╗Ö bß╗¤i ─æß║Īo diß╗ģn c├│ thß╗ā sß║»p ─æß║Ęt ├Īnh s├Īng v├Ā x├Īc ─æß╗ŗnh vß╗ŗ tr├Ł cß╗¦a c├Īc diß╗ģn vi├¬n. Cho biß║┐t mß╗Öt ─æ├©n chiß║┐u ─æang gß╗Źi tr├¬n s├ón khß║źu mß╗Öt v├╣ng s├Īng b├¬n trong ─æŲ░ß╗Øng tr├▓n (C) c├│ phŲ░ŲĪng tr├¼nh \({\left( {x - 13} \right)^2} + {\left( {y - 4} \right)^2} = 16\)
a) T├¼m tß╗Źa ─æß╗Ö t├óm v├Ā b├Īn k├Łnh cß╗¦a ─æŲ░ß╗Øng tr├▓n (C)
b) Cho biß║┐t tß╗Źa ─æß╗Ö tr├¬n s├ón khß║źu cß╗¦a 3 diß╗ģn vi├¬n A, B, C nhŲ░ sau: \(A(11;4).B(8;5),C(15;5)\).Diß╗ģn vi├¬n n├Āo ─æang ─æŲ░ß╗Żc ─æ├©n chiß║┐u s├Īng?
-
Hoß║Īt ─æß╗Öng kh├Īm ph├Ī 2 trang 61 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
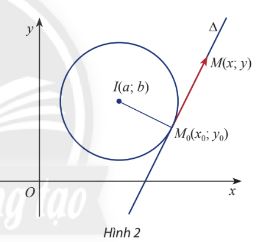
Cho ─æiß╗ām \({M_0}\left( {{x_0};{y_0}} \right)\) nß║▒m tr├¬n ─æŲ░ß╗Øng tr├▓n \((C)\) t├óm \(I(a;b)\)v├Ā cho ─æiß╗ām\(M(x;y)\) t├╣y ├Į trong mß║Ęt phß║│ng Oxy. Gß╗Źi \(\Delta \) l├Ā tiß║┐p tuyß║┐n vß╗øi \((C)\) tß║Īi \({M_0}\)
a) Viß║┐t biß╗āu thß╗®c tß╗Źa ─æß╗Ö cß╗¦a hai vt \(\overrightarrow {{M_0}M} \) v├Ā \(\overrightarrow {{M_0}I} \)
b) Viß║┐t biß╗āu thß╗®c tß╗Źa ─æß╗Ö cß╗¦a t├Łch v├┤ hŲ░ß╗øng cß╗¦a hai vt \(\overrightarrow {{M_0}M} \) v├Ā \(\overrightarrow {{M_0}I} \)
c) PhŲ░ŲĪng tr├¼nh \(\overrightarrow {{M_0}M} .\overrightarrow {{M_0}I} = 0\)l├Ā phŲ░ŲĪng tr├¼nh cß╗¦a ─æŲ░ß╗Øng thß║│ng n├Āo?
-
Thß╗▒c h├Ānh 3 trang 62 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Viß║┐t phŲ░ŲĪng tr├¼nh tiß║┐p tuyß║┐n cß╗¦a ─æŲ░ß╗Øng tr├▓n \((C):{x^2} + {y^2} - 2x - 4y - 20 = 0\) tß║Īi ─æiß╗ām \(A(4;6)\)
-
Vß║Łn dß╗źng 3 trang 62 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
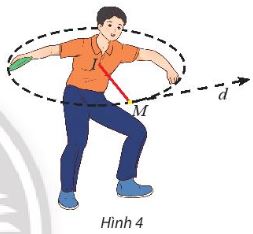
Mß╗Öt vß║Łn ─æß╗Öng vi├¬n n├®m ─æ─®a ─æ├Ż vung ─æ─®a theo mß╗Öt ─æŲ░ß╗Øng tr├▓n \((C)\) c├│ phŲ░ŲĪng tr├¼nh:
\({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = \frac{{169}}{{144}}\).
Khi ngŲ░ß╗Øi ─æ├│ vung ─æ─®a ─æß║┐n vß╗ŗ tr├Ł ─æiß╗ām \(M\left( {\frac{{17}}{{12}};2} \right)\) th├¼ bu├┤ng ─æ─®a (h├¼nh 4). Viß║┐t phŲ░ŲĪng tr├¼nh tiß║┐p tuyß║┐n cß╗¦a ─æŲ░ß╗Øng tr├▓n \((C)\) tß║Īi ─æiß╗ām M
-
Giß║Żi b├Āi 1 trang 62 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
PhŲ░ŲĪng tr├¼nh n├Āo trong c├Īc phŲ░ŲĪng tr├¼nh sau ─æ├óy l├Ā phŲ░ŲĪng tr├¼nh ─æŲ░ß╗Øng tr├▓n? T├¼m tß╗Źa ─æß╗Ö t├óm v├Ā b├Īn k├Łnh cß╗¦a ─æŲ░ß╗Øng tr├▓n ─æ├│.
a) \({x^2} + {y^2} - 6x - 8y + 21 = 0\)
b) \({x^2} + {y^2} - 2x + 4y + 2 = 0\)
c) \({x^2} + {y^2} - 3x + 2y + 7 = 0\)
d) \(2{x^2} + 2{y^2} + x + y - 1
-
Giß║Żi b├Āi 2 trang 62 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Lß║Łp phŲ░ŲĪng tr├¼nh ─æŲ░ß╗Øng tr├▓n trong c├Īc trŲ░ß╗Øng hß╗Żp sau:
a) \((C)\) c├│ t├óm \(I(1;5)\) v├Ā b├Īn k├Łnh \(r = 4\)
b) \((C)\) c├│ ─æŲ░ß╗Øng k├Łnh MN vß╗øi \(M(3; - 1)\)v├Ā \(N(9;3)\)
c) \((C)\) c├│ t├óm \(I(2;1)\) v├Ā tiß║┐p x├║c vß╗øi ─æŲ░ß╗Øng thß║│ng \(5x - 12y + 12 = 0\)
d) \((C)\) c├│ t├óm \(A(1; - 2)\) v├Ā ─æi qua ─æiß╗ām \(B(4; - 5)\)
-
Giß║Żi b├Āi 3 trang 62 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Lß║Łp phŲ░ŲĪng tr├¼nh ─æŲ░ß╗Øng tr├▓n ngoß║Īi tiß║┐p tam gi├Īc c├│ tß╗Źa ─æß╗Ö c├Īc ─æß╗ēnh l├Ā:
a) \(M(2;5),N(1;2),P(5;4)\)
b) \(A(0;6),B(7;7),C(8;0)\)
-
Giß║Żi b├Āi 4 trang 62 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Lß║Łp phŲ░ŲĪng tr├¼nh ─æŲ░ß╗Øng tr├▓n tiß║┐p x├║c vß╗øi hai trß╗źc tß╗Źa ─æß╗Ö Ox, Oy v├Ā ─æi qua ─æiß╗ām \(A(4;2)\)
-
Giß║Żi b├Āi 5 trang 63 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Cho ─æŲ░ß╗Øng tr├▓n \((C)\) c├│ phŲ░ŲĪng tr├¼nh \({x^2} + {y^2} - 2x - 4y - 20 = 0\)
a) Chß╗®ng tß╗Å rß║▒ng ─æiß╗ām \(M(4;6)\) thuß╗Öc ─æŲ░ß╗Øng tr├▓n \((C)\)
b) Viß║┐t phŲ░ŲĪng tr├¼nh tiß║┐p tuyß║┐n cß╗¦a \((C)\) tß║Īi ─æiß╗ām \(M(4;6)\)
c) Viß║┐t phŲ░ŲĪng tr├¼nh tiß║┐p tuyß║┐n cß╗¦a \((C)\)song song vß╗øi ─æŲ░ß╗Øng thß║│ng \(4x + 3y + 2022 = 0\)
-
Giß║Żi b├Āi 6 trang 63 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
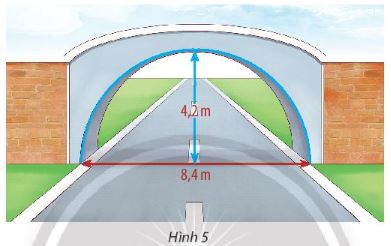
Mß╗Öt c├Īi cß║¦u h├¼nh b├Īn nguyß╗ćt rß╗Öng 8,4 m cao 4,2 m nhŲ░ h├¼nh 5. Mß║Ęt ─æŲ░ß╗Øng dŲ░ß╗øi cß╗Öng ─æŲ░ß╗Żc chia th├Ānh hai l├Ān cho xe ra v├Āo.
a) Vß║┐t phŲ░ŲĪng tr├¼nh m├┤ phß╗Ång c├Īi cß╗Ģng.
b) Mß╗Öt chiß║┐c xe tß║Żi rß╗Öng 2,2 m v├Ā cao 2,6 m ─æi ─æ├║ng l├Ān ─æŲ░ß╗Øng quy ─æß╗ŗnh c├│ thß╗ā ─æi qua cß╗Ģng v├Ā kh├┤ng l├Ām hŲ░ hß╗Ång cß╗Ģng hay kh├┤ng?
-
Giß║Żi B├Āi 1 trang 69 SBT To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
PhŲ░ŲĪng tr├¼nh n├Āo trong c├Īc phŲ░ŲĪng tr├¼nh sau ─æ├óy l├Ā phŲ░ŲĪng tr├¼nh ─æŲ░ß╗Øng tr├▓n? T├¼m tß╗Źa ─æß╗Ö t├óm v├Ā b├Īn k├Łnh cß╗¦a ─æŲ░ß╗Øng tr├▓n ─æ├│.
a) \({x^2} + {y^2} + 2x + 2y - 9 = 0\)
b) \({x^2} + {y^2} - 6x - 2y + 1 = 0\)
c) \({x^2} + {y^2} + 8x + 4y + 2022 = 0\)
d) \(3{x^2} + 2{y^2} + 5x + 7y - 1 = 0\)
-
Giß║Żi B├Āi 2 trang 70 SBT To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Lß║Łp phŲ░ŲĪng tr├¼nh ─æŲ░ß╗Øng tr├▓n \(\left( C \right)\) trong c├Īc trŲ░ß╗Øng hß╗Żp sau:
a) \(\left( C \right)\) c├│ t├óm \(O\left( {0;0} \right)\) v├Ā b├Īn k├Łnh \(R = 9\)
b) \(\left( C \right)\)c├│ ─æŲ░ß╗Øng k├Łnh AB vß╗øi \(A\left( {1;1} \right)\) v├Ā \(B\left( {3;5} \right)\)
c) \(\left( C \right)\) c├│ t├óm \(M\left( {2;3} \right)\) v├Ā tiß║┐p x├║c vß╗øi ─æŲ░ß╗Øng thß║│ng \(3x - 4y + 9 = 0\)
d) \(\left( C \right)\) c├│ t├óm \(I\left( {3;2} \right)\) v├Ā ─æi qua ─æiß╗ām \(B\left( {7;4} \right)\)
-
Giß║Żi B├Āi 3 trang 70 SBT To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Lß║Łp phŲ░ŲĪng tr├¼nh ─æŲ░ß╗Øng tr├▓n ngoß║Īi tiß║┐p tam gi├Īc c├│ tß╗Źa ─æß╗Ö c├Īc ─æß╗ēnh l├Ā:
a) \(A\left( {1;4} \right),B\left( {0;1} \right),C\left( {4;3} \right)\)
b) \(O\left( {0;0} \right),P\left( {16;0} \right),R\left( {0;12} \right)\)
-
Giß║Żi B├Āi 4 trang 70 SBT To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Lß║Łp phŲ░ŲĪng tr├¼nh ─æŲ░ß╗Øng tr├▓n tiß║┐p x├║c vß╗øi hai trß╗źc tß╗Źa ─æß╗Ö \(Ox,Oy\) v├Ā ─æi qua ─æiß╗ām \(A\left( {2;1} \right)\)
-
Giß║Żi B├Āi 5 trang 70 SBT To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Cho ─æŲ░ß╗Øng tr├▓n \(\left( C \right)\) c├│ phŲ░ŲĪng tr├¼nh \({x^2} + {y^2} - 6x - 2y - 15 = 0\)
a) Chß╗®ng tß╗Å rß║▒ng ─æiß╗ām \(A\left( {0;5} \right)\) thuß╗Öc ─æŲ░ß╗Øng tr├▓n \(\left( C \right)\)
b) Viß║┐t phŲ░ŲĪng tr├¼nh tiß║┐p tuyß║┐n vß╗øi \(\left( C \right)\) tß║Īi ─æiß╗ām \(A\left( {0;5} \right)\)
c) Viß║┐t phŲ░ŲĪng tr├¼nh tiß║┐p tuyß║┐n vß╗øi \(\left( C \right)\) song song vß╗øi ─æŲ░ß╗Øng thß║│ng \(8x + 6y + 99 = 0\)
-
Giß║Żi B├Āi 6 trang 70 SBT To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Mß╗Öt c├Īi cß╗Ģng b├Īn nguyß╗ćt rß╗Öng 6,8m, cao 3,4m. Mß║Ęt ─æŲ░ß╗Øng dŲ░ß╗øi cß╗Ģng ─æŲ░ß╗Żc chia th├Ānh hai l├Ān cho xe ra v├Āo
a) Viß║┐t phŲ░ŲĪng tr├¼nh m├┤ phß╗Ång c├Īi cß╗Ģng
b) Mß╗Öt chiß║┐c xe tß║Żi rß╗Öng 2,4 m v├Ā cao 2,5 m ─æi ─æ├║ng l├Ān ─æŲ░ß╗Øng quy ─æß╗ŗnh c├│ thß╗ā ─æi qua cß╗Ģng ─æŲ░ß╗Żc hay kh├┤ng?