Hướng dẫn Giải bài tập Toán 10 Chân trời sáng tạo Chương 9 Bài 2 Đường thẳng trong mặt phẳng tọa độ giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
Hoạt động khởi động trang 46 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
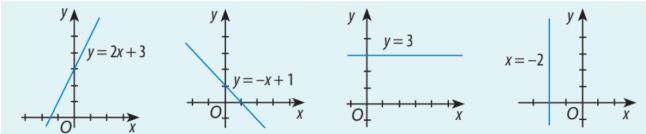
Tìm các giác trị của tham số a, b, c để phương trình ax + by + c = 0 có thể biểu diễn được các đường thẳng dưới đây.
-
Hoạt động khám phá 1 trang 46 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
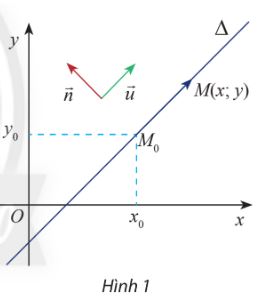
Trong mặt phẳng Oxy, cho hai đường thẳng \(\Delta \) đi qua điểm \({M_0}\left( {{x_0};{y_0}} \right)\) và vectơ \(\overrightarrow n = \left( {a;b} \right)\) và \(\overrightarrow u = \left( {b; - a} \right)\) khác vectơ 0. Cho biết \(\overrightarrow u \) có giá song song hoặc trùng với \(\Delta \).
a) Tính tích vô hướng \(\overrightarrow n \overrightarrow {.u} \) và nêu nhận xét về phương của hai vectơ \(\overrightarrow n ,\overrightarrow u \)
b) Gọi \(M\left( {x;y} \right)\) là điểm di động trên \(\Delta \). Chứng tỏ rằng vectơ \(\overrightarrow {{M_0}M} \) luôn cùng phương với vectơ \(\overrightarrow u \) và luôn vuông góc với vectơ \(\overrightarrow n \)
-
Hoạt động khám phá 2 trang 47 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Trong mặt phẳng Oxy, cho đường thẳng \(\Delta \) đi qua điểm \({M_0}\left( {{x_0};{y_0}} \right)\) và nhận \(\overrightarrow u = \left( {{u_1};{u_2}} \right)\) là vectơ chỉ phương. Với mỗi điểm \(M\left( {x;y} \right)\) thuộc \(\Delta \), tìm tọa độ của điểm M theo tọa độ của \({M_0}\) và \(\overrightarrow u \)
-
Thực hành 1 trang 47 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
a) Viết phương trình tham số của đường thẳng d đi qua điểm \(B( - 9;5)\) và nhận \(\overrightarrow v = (8; - 4)\) là vectơ chỉ phương
b) Tìm tọa độ điểm P trên \(\Delta \),biết P có tung độ bằng 1.
-
Vận dụng 1 trang 48 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
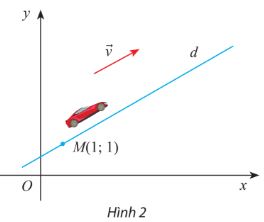
Một trò chơi đua xe ô tô vượt da mặt trên máy tính là xác định trước một hệ trục tọa độ Oxy. Cho biết một ô tô chuyển động thẳng đều từ điểm \(M(1;1)\) với Vectơ vận tốc\(\overrightarrow v = (40;30)\)
a) Viết phương trình tham số của đường thẳng d biểu diễn đường đi của ô tô
b) Tìm tọa độ của xe tương ứng với t = 2; t = 4
-
Hoạt động khám phá 3 trang 48 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Trong mặt phẳng Oxy, cho đường thẳng \(\Delta \) đi qua điểm \({M_0}\left( {{x_0};{y_0}} \right)\) và nhận \(\overrightarrow n = \left( {a;b} \right)\) làm vectơ pháp tuyến. Với mỗi điểm \(M\left( {x;y} \right)\) thuộc \(\Delta \), chứng tỏ rằng điểm \(M\left( {x;y} \right)\) có tọa độ thỏa mãn phương trình:
\(ax + by + c = 0\) (với \(c = - a{x_0} - b{y_0}\))
-
Thực hành 2 trang 49 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Viết phương trình tham số và phương trình tổng quát của đường thẳng \(\Delta \) trong các trường hợp sau:
a) Đường thẳng \(\Delta \) đi qua điểm \(A(1;1)\)và có vectơ pháp tuyến \(\overrightarrow n = \left( {3;5} \right)\)
b) Đường thẳng \(\Delta \) đi qua gốc tọa độ \(O(0;0)\)và có vectơ chỉ phương \(\overrightarrow u = \left( {2; - 7} \right)\)
c) Đường thẳng \(\Delta \) đi qua hai điểm \(M(4;0),N(0;3)\)
-
Vận dụng 2 trang 49 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Một người đã lập trình một trò chơi trên máy tính. Trên màn hình máy tính đã xác định trước một hệ trục tọa độ Oxy. Người đó viết lệnh để một điểm \(M(x;y)\) từ vị trí \(A(1;2)\) chuyển động thẳng đều với Vectơ vận tốc \(\overrightarrow v = (3; - 4)\)
a) Viết phương trình tổng quát của đường thẳng \(\Delta \) biểu diễn đường đi của điểm M
b) Tìm tọa độ của điểm M khi \(\Delta \) cắt trục hoành
-
Thực hành 3 trang 51 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Tìm các hàm số bậc nhất có đồ thị là các đường thẳng trong thực hành 2
-
Vận dụng 3 trang 51 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Một người bắt đầu mở một vòi nước. Nước từ vòi chảy với vận tốc là 2 \({m^3}/h\) vào một cái bể đã chứa sẵn 5 \({m^3}\) nước.
a) Viết biểu thức tính thể tích y của nước có trong bể sau x giờ
b) Gọi \(y = f(x)\)là hàm số xác định được từ câu a). Vẽ đồ thị d của hàm số này
c) Viết phương trình tham số và phương trình tổng quát của đường thẳng d
-
Hoạt động khám phá 4 trang 51 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
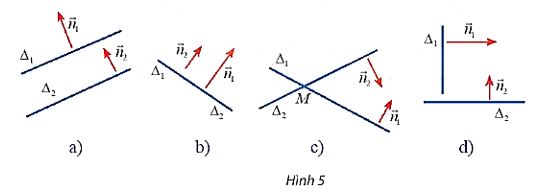
Cho hai đường thẳng \({\Delta _1}\)và \({\Delta _2}\) một vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \)
Nêu nhận xét về vị trí tương đối giữa \({\Delta _1}\)và \({\Delta _2}\) trong các trường hợp sau:
a) \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) cùng phương (hình 5a,b)
b) \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) không cùng phương (hình 5c,d)
c) \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \)vuông góc (hình 5d)
-
Thực hành 4 trang 53 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Xét vị trí tương đối của các cặp đường thẳng \({d_1}\)và \({d_2}\) trong các trường hợp sau:
a) \({d_1}:x - 5y + 9 = 0\) và \({d_2}:10x + 2y + 7 = 10\)
b) \({d_1}:3x - 4y + 9 = 0\) và \({d_2}:\left\{ \begin{array}{l}x = 1 + 4t\\y = 1 + 3t\end{array} \right.\)
c) \({d_1}:\left\{ \begin{array}{l}x = 5 + 4t\\y = 4 + 3t\end{array} \right.\) và \({d_2}:\left\{ \begin{array}{l}x = 1 + 8t\\y = 1 + 6t\end{array} \right.\)
-
Vận dụng 4 trang 53 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Viết phương trình đường thẳng \({d_1}\):
a) Đi qua điểm \(A(2;3)\) và song song với đường thẳng \({d_2}:x + 3y + 2 = 0\)
b) Đi qua điểm \(B(4; - 1)\) và vuông góc với đường thẳng \({d_3}:3x - y + 1 = 0\)
-
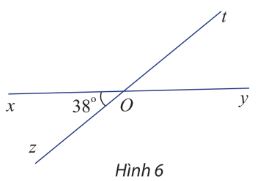
Hoạt động khám phá 5 trang 54 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Cho hai đường thẳng xy và zt cắt nhau tại O và cho biết \(\widehat {xOz} = 38^\circ \) (hình 6)
Tính số đo các góc \(\widehat {xOt},\widehat {tOy}\) và \(\widehat {yOz}\)
-
Hoạt động khám phá 6 trang 54 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Cho hai đường thẳng
\({\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0\) (\({a_1}^2 + {b_1}^2 > 0\)) và \({\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0\) \(\left( {{a_2}^2 + {b_2}^2 > 0} \right)\)
có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \).
Tìm tọa độ \(\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} \)và tính \(\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)\)
-
Thực hành 5 trang 56 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Tìm số đo của góc giữa hai đường thẳng \({\Delta _1}\)và \({\Delta _2}\) trong các trường hợp sau
a) \({\Delta _1}:x + 3y - 7 = 0\) và \({\Delta _2}:x - 2y + 3 = 0\)
b) \({\Delta _1}:4x - 2y + 5 = 0\) và \({\Delta _2}:\left\{ \begin{array}{l}x = t\\y = 13 + 2t\end{array} \right.\)
c) \({\Delta _1}:\left\{ \begin{array}{l}x = 1 + t\\y = 3 + 2t\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = - 7 + 2t\\y = 1 - t\end{array} \right.\)
-
Vận dụng 5 trang 56 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Tìm số đo của góc giữa hai đường thẳng là đồ thị của hai hàm số \(y = x\) và \(y = 2x + 1\)
-
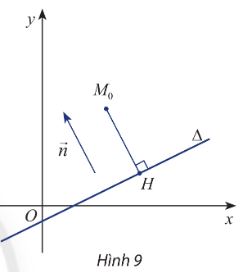
Hoạt động khám phá 7 trang 56 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Trong mặt phẳng Oxy. Cho đường thẳng \(\Delta :ax + by + c = 0\left( {{a^2} + {b^2} > 0} \right)\) có vectơ pháp tuyến \(\overrightarrow n \) và cho điểm \({M_0}\left( {{x_0};{y_0}} \right)\)có hình chiếu vuông góc \(H\left( {{x_H};{y_H}} \right)\)trên \(\Delta \)(hình 9).
a) Chứng minh rằng hai vectơ \(\overrightarrow n \) và \(\overrightarrow {H{M_0}} \)cùng phương và tìm tọa độ của chúng
b) Gọi p là tích vô hướng của hai vectơ \(\overrightarrow n \) và \(\overrightarrow {H{M_0}} \).
Chứng minh rằng \(p = a{x_0} + b{y_0} + c\)
c) Giải thích công thức \(\left| {\overrightarrow {H{M_0}} } \right| = \frac{{\left| p \right|}}{{\left| {\overrightarrow n } \right|}}\)
-
Thực hành 6 trang 57 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Trong mặt phẳng Oxy, cho tam giác ABC có tọa độ các đỉnh là \(A(1;1),B(5;2),C(4;4)\). Tính độ dài các đường cao của tam giác ABC
-
Vận dụng 6 trang 57 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Tính khoảng cách giữa hai đường thẳng \({d_1}:4x - 3y + 2 = 0\) và \({d_2}:4x - 3y + 12 = 0\)
-
Giải bài 1 trang 57 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Lập phương trình tham số và phương trình tổng quát của đường thẳng d trong mỗi trường hợp sau:
a) d đi qua điểm \(A( - 1;5)\) và có vectơ chỉ phương \(\overrightarrow u = (2;1)\)
b) d đi qua điểm \(B(4; - 2)\) và có vectơ pháp tuyến là \(\overrightarrow n = (3; - 2)\)
c) d đi qua \(P(1;1)\) và có hệ số góc \(k = - 2\)
d) d đi qua hai điểm \(Q(3;0)\)và \(R(0;2)\)
-
Giải bài 2 trang 57 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Cho tam giác ABC biết \(A(2;5),B(1;2)\) và \(C(5;4)\)
a) Lập phương trình tổng quát của đường thẳng BC
b) Lập phương trình tham số của đường trung tuyến AM
c) Lập phương trình của đường cao AH
-
Giải bài 3 trang 57 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Lập phương trình tham số và phương trình tổng quát của đường thẳng \(\Delta \) trong mỗi trường hợp sau:
a) \(\Delta \) đi qua \(A(2;1)\) và song song với đường thẳng \(3x + y + 9 = 0\)
b) \(\Delta \)đi qua \(B( - 1;4)\) và vuông góc với đường thẳng \(2x - y - 2 = 0\)
-
Giải bài 4 trang 57 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Xét vị trí tương đối của cặp đường thẳng \({d_1}\)và \({d_2}\) sau đây:
a) \({d_1}:x - y + 2 = 0\) và \({d_2}:x + y + 4 = 0\)
b) \({d_1}:\left\{ \begin{array}{l}x = 1 + 2t\\y = 3 + 5t\end{array} \right.\) và \({d_2}:5x - 2y + 9 = 0\)
c) \({d_1}:\left\{ \begin{array}{l}x = 2 - t\\y = 5 + 3t\end{array} \right.\) và \({d_2}:3x + y - 11 = 0\)
-
Giải bài 5 trang 58 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Cho đường thẳng d có phương trình tham số \(\left\{ \begin{array}{l}x = 2 - t\\y = 5 + 3t\end{array} \right.\)
Tìm giao điểm của d với hai trục tọa độ
-
Giải bài 6 trang 58 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Tìm số đo của góc giữa hai đường thẳng \({d_1}\) và \({d_2}\) trong các trường hợp sau:
a) \({d_1}:x - 2y + 3 = 0\) và \({d_2}:3x - y - 11 = 0\)
b) \({d_1}:\left\{ \begin{array}{l}x = t\\y = 3 + 5t\end{array} \right.\) và \({d_2}:x + 5y - 5 = 0\)
c) \({d_1}:\left\{ \begin{array}{l}x = 3 + 2t\\y = 7 + 4t\end{array} \right.\) và \({d_2}:\left\{ \begin{array}{l}x = t\\y = - 9 + 2t\end{array} \right.\)
-
Giải bài 7 trang 58 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Tính khoảng cách từ điểm M đến đường thẳng \(\Delta \) trong các trường hợp sau:
a) \(M(1;2)\) và \(\Delta :3x - 4y + 12 = 0\)
b) \(M(4;4)\) và \(\Delta :\left\{ \begin{array}{l}x = t\\y = - t\end{array} \right.\)
c) \(M(0;5)\) và \(\Delta :\left\{ \begin{array}{l}x = t\\y = \frac{{ - 19}}{4}\end{array} \right.\)
d) \(M(0;0)\) và \(\Delta :3x + 4y - 25 = 0\)
-
Giải bài 8 trang 58 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Tính khoảng cách giữa hai đường thẳng \(\Delta :3x + 4y - 10 = 0\) và \(\Delta ':6x + 8y - 1 = 0\)
-
Giải bài 9 trang 58 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Trong mặt phẳng Oxy cho điểm \(S(x;y)\) di động trên đường thẳng \(d:12x - 5y + 16 = 0\). Tính khoảng cách ngắn nhất từ điểm \(M(5;10)\) đến điểm S.
-
Giải bài 10 trang 58 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Một người đang viết chương trình cho trò chơi đá bóng robot. Gọi \(A( - 1;1),B(9;6),C(5; - 3)\) là 3 vị trí trên màn hình
a) Viết phương trình các đường thẳng AB, AC, BC
b) Tính góc hợp bởi hai đường thẳng AB và AC
c) Tính khoảng cách từ điểm A đến đường thẳng BC
-
Giải Bài 1 trang 65 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Tìm các giá trị của tham số a, b, c để phương trình \(ax + by + c = 0\) có thể biểu diễn được các đường thẳng trong hình dưới đây

-
Giải Bài 2 trang 65 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Lập phương trình tổng quát và phương trình tham số của đường thẳng d trong mỗi trường hợp sau:
a) d đi qua điểm \(M\left( {2;2} \right)\) và vectơ chỉ phương \(\overrightarrow u = \left( {4;7} \right)\)
b) d đi qua điểm \(N\left( {0;1} \right)\) và có vectơ pháp tuyến là \(\overrightarrow n = \left( { - 5;3} \right)\)
c) d đi qua \(A\left( { - 2; - 3} \right)\) và có hệ số góc \(k = 3\)
d) d đi qua hai điểm \(P\left( {1;1} \right),Q\left( {3;4} \right)\)
-
Giải Bài 3 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Cho tam giác ABC, biết \(A\left( {1;4} \right),B\left( {0;1} \right),C\left( {4;3} \right)\)
a) Lập phương trình tổng quát của đường thẳng BC
b) Lập phương trình tham số của đường trung tuyến AM
c) Lập phương trình tổng quát của đường cao AH
-
Giải Bài 4 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Lập phương trình tổng quát của đường thẳng \(\Delta \) trong mỗi trường hợp sau:
a) \(\Delta \) đi qua \(M\left( {3;3} \right)\) và song song với đường thẳng \(x + 2y - 2022 = 0\)
b) \(\Delta \) đi qua \(N\left( {2; - 1} \right)\) và vuông góc với đường thẳng \(3x + 2y + 99 = 0\)
-
Giải Bài 5 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Xét vị trí tương đối của các cặp đường thẳng \({d_1}\) và \({d_2}\) sau đây:
a) \({d_1}:2x + y + 9 = 0\) và \({d_2}:2x + 3y - 9 = 0\)
b) \({d_1}:\left\{ \begin{array}{l}x = 2 + t\\y = 1 - 2t\end{array} \right.\) và \({d_2}:2x + y + 10 = 0\)
c) \({d_1}:\left\{ \begin{array}{l}x = 1 - t\\y = 8 - 5t\end{array} \right.\) và \({d_2}:5x - y + 3 = 0\)
-
Giải Bài 6 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Cho đường thẳng d có phương trình tham số \(\left\{ \begin{array}{l}x = 1 + t\\y = 2 + 2t\end{array} \right.\)
Tìm giao điểm của d với đường thẳng \(\Delta :x + y - 2 = 0\)
-
Giải Bài 7 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Tìm số đo của góc giữa hai đường thẳng \({d_1}\) và \({d_2}\) trong các trường hợp sau:
a) \({d_1}:5x - 3y + 1 = 0\) và \({d_2}:10x - 6y - 7 = 0\)
b) \({d_1}:7x - 3y + 7 = 0\) và \({d_2}:3x + 7y - 10 = 0\)
c) \({d_1}:2x - 4y + 9 = 0\) và \({d_2}:6x - 2y - 2023 = 0\)
-
Giải Bài 7 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Tìm số đo của góc giữa hai đường thẳng \({d_1}\) và \({d_2}\) trong các trường hợp sau:
a) \({d_1}:5x - 3y + 1 = 0\) và \({d_2}:10x - 6y - 7 = 0\)
b) \({d_1}:7x - 3y + 7 = 0\) và \({d_2}:3x + 7y - 10 = 0\)
c) \({d_1}:2x - 4y + 9 = 0\) và \({d_2}:6x - 2y - 2023 = 0\)
-
Giải Bài 8 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Tính khoảng cách từ điểm M đến đường thẳng \(\Delta \) trong các trường hợp sau:
a) \(M\left( {2;3} \right)\) và \(\Delta :8x - 6y + 7 = 0\)
b) \(M\left( {0;1} \right)\) và \(\Delta :4x + 9y - 20 = 0\)
c) \(M\left( {1;1} \right)\) và \(\Delta :3y - 5 = 0\)
d) \(M\left( {4;9} \right)\) và \(\Delta :x - 25 = 0\)
-
Giải Bài 9 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Tìm c để đường thẳng \(\Delta :4x - 3y + c = 0\) tiếp xúc với đường tròn \(\left( C \right)\) có \(J\left( {1;2} \right)\) và bán kính \(R = 3\)
-
Giải Bài 10 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Tính khoảng cách giữa hai đường thẳng: \(\Delta :6x + 8y - 11 = 0\) và \(\Delta ':6x + 8y - 1 = 0\)
-
Giải Bài 11 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Một trạm viễn thông \(S\) có tọa độ \(\left( {5;1} \right)\). Một người đang ngồi trên chiếc xe khách chạy trên đoạn cao tốc có dạng một đường thẳng \(\Delta \) có phương trình \(12x + 5y - 20 = 0\). Tính khoảng cách ngắn nhất giữa người đó và trạm viễn thông \(S\). Biết rằng mỗi đơn vị độ dài tương ứng với 1 km.