Hoạt động khám phá 1 trang 46 SGK Toán 10 Chân trời sáng tạo tập 2
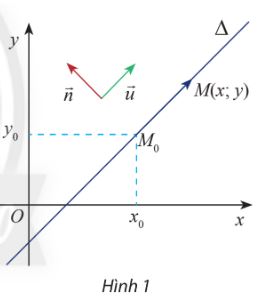
Trong mặt phẳng Oxy, cho hai đường thẳng \(\Delta \) đi qua điểm \({M_0}\left( {{x_0};{y_0}} \right)\) và vectơ \(\overrightarrow n = \left( {a;b} \right)\) và \(\overrightarrow u = \left( {b; - a} \right)\) khác vectơ 0. Cho biết \(\overrightarrow u \) có giá song song hoặc trùng với \(\Delta \).
a) Tính tích vô hướng \(\overrightarrow n \overrightarrow {.u} \) và nêu nhận xét về phương của hai vectơ \(\overrightarrow n ,\overrightarrow u \)
b) Gọi \(M\left( {x;y} \right)\) là điểm di động trên \(\Delta \). Chứng tỏ rằng vectơ \(\overrightarrow {{M_0}M} \) luôn cùng phương với vectơ \(\overrightarrow u \) và luôn vuông góc với vectơ \(\overrightarrow n \)
Hướng dẫn giải chi tiết Hoạt động khám phá 1
Phương pháp giải
a) +) Áp dụng ứng dụng biểu thức tọa độ của vectơ tính tích vô hướng
+) Dựa vào kết quả tích vô hướng các định phương (bằng 0 thì vuông góc)
b) +) Xác định tỉ lệ giũa các tọa độ của hai vectơ để so sánh về phương
+) Tính tích vô hướng để chứng minh vuông góc
Lời giải chi tiết
a) Ta có \(\overrightarrow n .\overrightarrow u = a.b + b.( - a) = 0\)
Tích vô hướng bằng 0 nên hai vectơ \(\overrightarrow n ,\overrightarrow u \)có phương vuông góc với nhau
b) Vectơ \(\overrightarrow {{M_0}M} \) có giá là đường thẳng \(\Delta\)
=> luôn cùng phương với vectơ \(\overrightarrow u \)
=> vectơ \(\overrightarrow {{M_0}M} \) có phương vuông góc với vectơ \(\overrightarrow n \)
-- Mod Toán 10 HỌC247
-


Trong mặt phẳng toạ độ Oxy, cho hai điểm A(4 ; −2), B(10; 4) và điểm M nằm trên trục Ox. Tìm toạ độ điểm M sao cho \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right|\) có giá trị nhỏ nhất.
bởi Bao Nhi
 25/11/2022
Theo dõi (0) 1 Trả lời
25/11/2022
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Hoạt động khởi động trang 46 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 2 trang 47 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Thực hành 1 trang 47 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Vận dụng 1 trang 48 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 3 trang 48 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Thực hành 2 trang 49 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Vận dụng 2 trang 49 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Thực hành 3 trang 51 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Vận dụng 3 trang 51 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 4 trang 51 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Thực hành 4 trang 53 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Vận dụng 4 trang 53 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 5 trang 54 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 6 trang 54 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Thực hành 5 trang 56 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Vận dụng 5 trang 56 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 7 trang 56 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Thực hành 6 trang 57 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Vận dụng 6 trang 57 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 1 trang 57 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 2 trang 57 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 3 trang 57 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 4 trang 57 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 5 trang 58 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 6 trang 58 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 7 trang 58 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 8 trang 58 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 9 trang 58 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 10 trang 58 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 1 trang 65 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 2 trang 65 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 3 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 4 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 5 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 6 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 7 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 7 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 8 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 9 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 10 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 11 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST