HÆ°áŧng dášŦn GiášĢi bà i tášp ToÃĄn 10 CÃĄnh Diáŧu ChÆ°ÆĄng 7 Bà i 4 Váŧ trà tÆ°ÆĄng Äáŧi và gÃģc giáŧŊa hai ÄÆ°áŧng thášģng - KhoášĢng cÃĄch táŧŦ máŧt Äiáŧm Äášŋn máŧt ÄÆ°áŧng thášģng giÚp cÃĄc em háŧc sinh nášŊm váŧŊng phÆ°ÆĄng phÃĄp giášĢi bà i tášp và Ãīn luyáŧn táŧt kiášŋn tháŧĐc.
-
Hoᚥt Äáŧng 1 trang 81 SGK ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
NÊu váŧ trà tÆ°ÆĄng Äáŧi cáŧ§a hai ÄÆ°áŧng thášģng trong máš·t phášģng.
-
Hoᚥt Äáŧng 2 trang 81 SGK ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
Trong máš·t phášģng toᚥ Äáŧ, cho hai ÄÆ°áŧng thášģng \({\Delta _1},{\Delta _2}\) lᚧn lÆ°áŧĢt cÃģ vectÆĄ cháŧ phÆ°ÆĄng là \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \). NÊu Äiáŧu kiáŧn váŧ hai vectÆĄ \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) trong mÃīi trÆ°áŧng háŧĢp sau:
a) \({\Delta _1}\) cášŊt \({\Delta _2}\)
b) \({\Delta _1}\)song song váŧi \({\Delta _2}\)
c), \({\Delta _1}\) trÃđng váŧi \({\Delta _2}\)
-
Luyáŧn tášp 1 trang 82 SGK ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
XÃĐt váŧ trà tÆ°ÆĄng Äáŧi cáŧ§a hai ÄÆ°áŧng thášģng \({\Delta _1}:\left\{ \begin{array}{l}x = 1 + {t_1}\\y = - 2 + {t_1}\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = 2{t_2}\\y = - 3 + 2{t_2}\end{array} \right.\)
-
Luyáŧn tášp 2 trang 82 SGK ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
XÃĐt váŧ trà tÆ°ÆĄng Äáŧi cáŧ§a ÄÆ°áŧng thášģng d: x + 2y â 2 = 0 váŧi máŧi ÄÆ°áŧng thášģng sau:
\({\Delta _1}{\rm{: }}3x{\rm{ }}--{\rm{ }}2y{\rm{ }} + {\rm{ }}6{\rm{ }} = {\rm{ }}0\); \({\Delta _2}:{\rm{ }}x{\rm{ }} + {\rm{ }}2y{\rm{ }} + {\rm{ }}2{\rm{ }} = {\rm{ }}0\); \({\Delta _3}:{\rm{ }}2x{\rm{ }} + {\rm{ }}4y{\rm{ }}--{\rm{ }}4{\rm{ }} = {\rm{ }}0.\)
-
Hoᚥt Äáŧng 3 trang 83 SGK ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
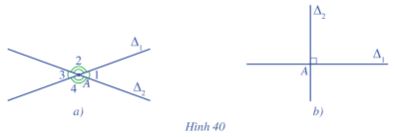
Trong máš·t phášģng, cho hai ÄÆ°áŧng thášģng \({\Delta _1}\) và \({\Delta _2}\) cášŊt nhau tᚥi A tᚥo thà nh báŧn gÃģc Äáŧnh A (quy Æ°áŧc khÃīng káŧ gÃģc bášđt và gÃģc khÃīng).
Quan sÃĄt HÃŽnh 40a và Äáŧc tÊn máŧt gÃģc nháŧn trong báŧn gÃģc ÄÃģ.
Quan sÃĄt HÃŽnh 40b và nÊu Äáš·c Äiáŧm báŧn gÃģc tᚥi Äáŧnh A.
-
Hoᚥt Äáŧng 4 trang 83 SGK ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
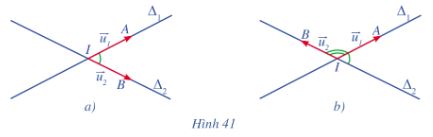
Cho hai ÄÆ°áŧng thášģng \({\Delta _1},{\Delta _2}\)cášŊt nhau tᚥi I và cÃģ vectÆĄ cháŧ phÆ°ÆĄng lᚧn lÆ°áŧĢt là \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \). Gáŧi A và B là cÃĄc Äiáŧm lᚧn lÆ°áŧĢt thuáŧc hai ÄÆ°áŧng thášģng \({\Delta _1}\) và \({\Delta _2}\) sao cho \(\overrightarrow {{u_1}} = \overrightarrow {IA} ,\overrightarrow {{u_2}} = \overrightarrow {IB} \).
a) Quan sÃĄt HÃŽnh 41a, HÃŽnh 41b, hÃĢy nhášn xÃĐt váŧ Äáŧ láŧn cáŧ§a gÃģc giáŧŊa hai ÄÆ°áŧng thášģng
\({\Delta _1},{\Delta _2}\)và Äáŧ láŧn cáŧ§a gÃģc giáŧŊa hai vectÆĄ \(\overrightarrow {IA} \),\(\overrightarrow {IB} \)
b) CháŧĐng táŧ cos(\({\Delta _1},{\Delta _2}\)) = \(\left| {cos\left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)} \right|\).
-
Hoᚥt Äáŧng 5 trang 84 SGK ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
Trong máš·t phášģng toᚥ Äáŧ, cho hai ÄÆ°áŧng thášģng \({\Delta _1}\) và \({\Delta _2}\) cÃģ vectÆĄ cháŧ phÆ°ÆĄng lᚧn lÆ°áŧĢt là \(\overrightarrow {{u_1}} = {\rm{ }}\left( {{a_1};{\rm{ }}{b_1}} \right),{\rm{ }}\overrightarrow {{u_2}} {\rm{ }} = {\rm{ }}\left( {{a_2};{b_2}} \right)\) . TÃnh \(\cos \left( {{\Delta _1},{\Delta _2}} \right)\).
-
Luyáŧn tášp 3 trang 84 SGK ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
TÃnh sáŧ Äo gÃģc giáŧŊa hai ÄÆ°áŧng thášģng \({\Delta _1}\) và \({\Delta _2}\) trong mÃīi trÆ°áŧng háŧĢp sau:
a) \({\Delta _1}:\left\{ \begin{array}{l}x = - 3 + 3\sqrt 3 t\\y = 2 + 3t\end{array} \right.\) và \({\Delta _2}:y - 4 = 0\)
b) \({\Delta _1}:2x - y = 0\) và \({\Delta _2}: - x + 3y - 5 = 0\)
-
Hoᚥt Äáŧng 6 trang 85 SGK ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
Trong máš·t phášģng toᚥ Äáŧ, cho ÄÆ°áŧng thášģng \(\Delta \): 2x + yâ 4 = 0 và Äiáŧm M(-1; 1). Gáŧi H là hÃŽnh chiášŋu cáŧ§a M lÊn ÄÆ°áŧng thášģng \(\Delta \).
a) TÃŽm máŧt vectÆĄ cháŧ phÆ°ÆĄng cáŧ§a ÄÆ°áŧng thášģng MH.
b) Viášŋt phÆ°ÆĄng trÃŽnh tham sáŧ cáŧ§a ÄÆ°áŧng thášģng MH.
c) TÃŽm toᚥ Äáŧ cáŧ§a H. TáŧŦ ÄÃģ, tÃnh Äáŧ dà i Äoᚥn thášģng MH.
-
Luyáŧn tášp 2 trang 84 SGK ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
a) TÃnh khoášĢng cÃĄch táŧŦ Äiáŧm \(O\left( {0{\rm{;}}0} \right)\) Äášŋn ÄÆ°áŧng thášģng \(\Delta \):\(\frac{x}{{ - 4}} + \frac{y}{2} = 1\)
b) TÃnh khoášĢng cÃĄch giáŧŊa hai ÄÆ°áŧng thášģng song song \({\Delta _1}:x - y + 1 = 0\)và \({\Delta _2}:x - y - 1 = 0\)
-
GiášĢi bà i 1 trang 86 SGK ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
XÃĐt váŧ trà tÆ°ÆĄng Äáŧi cáŧ§a máŧi cáš·p ÄÆ°áŧng thášģng sau
a) \({d_1}:3x + 2y--5 = 0\) và \({d_2}:x - 4y + 1 = 0\) ;
b) \({d_3}:x - 2y + 3 = 0\) và \({d_4}: - {\rm{ }}2x + 4y + 10 = 0\) ;
c) \({d_5}:4x + 2y - 3 = 0\) và \({d_6}:\left\{ \begin{array}{l}x = - \frac{1}{2} + t\\y = \frac{5}{2} - 2t\end{array} \right.\)
-
GiášĢi bà i 2 trang 86 SGK ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
TÃnh sáŧ Äo gÃģc giáŧŊa hai ÄÆ°áŧng thášģng \({d_1}:2x--y + 5 = 0\) và \({d_2}:x - 3y + 3 = 0\).
-
GiášĢi bà i 3 trang 86 SGK ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
TÃnh khoášĢng cÃĄch táŧŦ máŧt Äiáŧm Äášŋn máŧt ÄÆ°áŧng thášģng trong máŧi trÆ°áŧng háŧĢp sau:
a)\(A\left( {1; - 2} \right){\rm{ }}v\`a {\rm{ }}{\Delta _1}:{\rm{ }}3x - y + {\rm{ }}4{\rm{ }} = {\rm{ }}0\) ;
b) B(-3; 2) và \({\Delta _2}:\left\{ \begin{array}{l}x = - 2 + t\\y = 1 - 2t\end{array} \right.\)
-
GiášĢi bà i 4 trang 86 SGK ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
Váŧi giÃĄ tráŧ nà o cáŧ§a tham sáŧ m thÃŽ hai ÄÆ°áŧng thášģng sau ÄÃĒy vuÃīng gÃģc?
\({\Delta _1}:mx - y + 1 = 0\) và \({\Delta _2}:2x - y + 3 = 0\).
-
GiášĢi bà i 5 trang 86 SGK ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
Cho ba Äiáŧm A(2;- 1), B(1 ; 2) và C(4;- 2). TÃnh sáŧ Äo gÃģc BAC và gÃģc giáŧŊa hai ÄÆ°áŧng thášģng AB, AC.
-
GiášĢi bà i 6 trang 86 SGK ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
Cho ba Äiáŧm A(2;4), B(-1; 2) và C(3;-1). Viášŋt phÆ°ÆĄng trÃŽnh ÄÆ°áŧng thášģng Äi qua B Äáŧng tháŧi cÃĄch Äáŧu A và C.
-
GiášĢi bà i 7 trang 86 SGK ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
CÃģ hai con tà u A và B cÃđng xuášĨt phÃĄt táŧŦ hai bášŋn, chuyáŧn Äáŧng Äáŧu theo ÄÆ°áŧng thášģng ngoà i biáŧn. TrÊn mà n hÃŽnh ra Äa cáŧ§a trᚥm Äiáŧu khiáŧn (ÄÆ°áŧĢc coi nhÆ° máš·t phášģng toᚥ Äáŧ Oxy váŧi ÄÆĄn váŧ trÊn cÃĄc tráŧĨc tÃnh theo ki-lÃī-mÃĐt), sau khi xuášĨt phÃĄt t (giáŧ) (\(t \ge 0\)), váŧ trÃ
cáŧ§a tà u A cÃģ toᚥ Äáŧ ÄÆ°áŧĢc xÃĄc Äáŧnh báŧi cÃīng tháŧĐc \(\left\{ \begin{array}{l}x = 3 - 35t\\y = - 4 + 25t\end{array} \right.\) ,váŧ trà cáŧ§a tà u B cÃģ toᚥ Äáŧ là (4 â 30t; 3 â 40t).
a) TÃnh cÃīsin gÃģc giáŧŊa hai ÄÆ°áŧng Äi cáŧ§a hai tà u A và B.
b) Sau bao lÃĒu káŧ táŧŦ tháŧi Äiáŧm xuášĨt phÃĄt hai tà u gᚧn nhau nhášĨt?
c) Nášŋu tà u A ÄáŧĐng yÊn áŧ váŧ trà ban Äᚧu, tà u B chᚥy thÃŽ khoášĢng cÃĄch ngášŊn nhášĨt giáŧŊa hai tà u bášąng bao nhiÊu?
-
GiášĢi bà i 33 trang 81 SBT ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
PhÆ°ÆĄng trÃŽnh nà o dÆ°áŧi ÄÃĒy là phÆ°ÆĄng trÃŽnh tham sáŧ cáŧ§a máŧt ÄÆ°áŧng thášģng song song váŧi ÄÆ°áŧng thášģng: x â 2y + 3 = 0?
A. \(\left\{ \begin{array}{l}x = - 1 + 2t\\y = 1 + t\end{array} \right.\)
B. \(\left\{ \begin{array}{l}x = 1 + 2t\\y = - 1 + t\end{array} \right.\)
C. \(\left\{ \begin{array}{l}x = 1 + t\\y = - 1 - 2t\end{array} \right.\)
D. \(\left\{ \begin{array}{l}x = 1 - 2t\\y = - 1 + t\end{array} \right.\)
-
GiášĢi bà i 34 trang 81 SBT ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
PhÆ°ÆĄng trÃŽnh nà o dÆ°áŧi ÄÃĒy là phÆ°ÆĄng trÃŽnh tham sáŧ cáŧ§a máŧt ÄÆ°áŧng thášģng vuÃīng gÃģc váŧi ÄÆ°áŧng thášģng: \(\left\{ \begin{array}{l}x = - 1 + 3t\\y = 1 - 2t\end{array} \right.\)?
A. \(\left\{ \begin{array}{l}x = - 1 - 2t\\y = 1 - 3t\end{array} \right.\)
B. \(\left\{ \begin{array}{l}x = - 1 - 2t\\y = 1 + 3t\end{array} \right.\)
C. \(\left\{ \begin{array}{l}x = - 1 - 3t\\y = 1 + 2t\end{array} \right.\)
D. \(\left\{ \begin{array}{l}x = - 1 - 3t\\y = 1 - 2t\end{array} \right.\)
-
GiášĢi bà i 35 trang 81 SBT ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
ÄÆ°áŧng thášģng â Äi qua Äiáŧm M(â1 ; 2) và song song váŧi ÄÆ°áŧng thášģng d: 2x â y â 5 = 0 cÃģ phÆ°ÆĄng trÃŽnh táŧng quÃĄt là :
A. 2x â y = 0
B. 2x â y + 4 = 0
C. 2x + y + 4 = 0
D. x + 2y â 3 = 0
-
GiášĢi bà i 36 trang 81 SBT ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
ÄÆ°áŧng thášģng â Äi qua Äiáŧm M(3 ; -4) và vuÃīng gÃģc váŧi ÄÆ°áŧng thášģng d: x â 3y + 1 = 0 cÃģ phÆ°ÆĄng trÃŽnh táŧng quÃĄt là :
A. x - 3y â 15 = 0
B. -3x + y + 5 = 0
C. 3x + y â 13 = 0
D. 3x + y â 5 = 0
-
GiášĢi bà i 37 trang 81 SBT ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
Cho â1: x â 2y + 3 = 0 và â2: -2x â y + 5 = 0. Sáŧ Äo gÃģc giáŧŊa hai ÄÆ°áŧng thášģng â1 và â2 là :
A. 30â°
B. 45â°
C. 90°
D. 60â°
-
GiášĢi bà i 38 trang 82 SBT ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
Cho \({\Delta _1}:\left\{ \begin{array}{l}x = - 2 + \sqrt 3 t\\y = 1 - t\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = - 1 + \sqrt 3 t'\\y = 2 + t'\end{array} \right.\). Sáŧ Äo gÃģc giáŧŊa hai ÄÆ°áŧng thášģng â1 và â2 là :
A. 300
B. 450
C. 900
D. 600
-
GiášĢi bà i 39 trang 82 SBT ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
KhoášĢng cÃĄch táŧŦ Äiáŧm M(5 ; â 2) Äášŋn ÄÆ°áŧng thášģng â: - 3x + 2y + 6 = 0 là :
A. 13
B. \(\sqrt {13} \)
C. \(\frac{{\sqrt {13} }}{{13}}\)
D. \(2\sqrt {13} \)
-
GiášĢi bà i 40 trang 82 SBT ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
XÃĐt váŧ trà tÆ°ÆĄng Äáŧi cáŧ§a máŧi cáš·p ÄÆ°áŧng thášģng sau:
a) \({d_1}:2x - 3y + 5 = 0\) và \({d_2}:2x + y - 1 = 0\)
b) \({d_3}:\left\{ \begin{array}{l}x = - 1 - 3t\\y = 3 + t\end{array} \right.\) và \({d_4}:x + 3y - 5 = 0\)
c) \({d_5}:\left\{ \begin{array}{l}x = 2 - 2t\\y = - 1 + t\end{array} \right.\) và \({d_6}:\left\{ \begin{array}{l}x = - 2 + 2t'\\y = 1 - {t^'}\end{array} \right.\)
-
GiášĢi bà i 41 trang 82 SBT ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
TÃŽm sáŧ Äo gÃģc giáŧŊa hai ÄÆ°áŧng thášģng cáŧ§a máŧi cáš·p ÄÆ°áŧng thášģng sau:
a) â1: 3x + y - 5 = 0 và â2: x + 2y â 3 = 0
b) \({\Delta _3}:\left\{ \begin{array}{l}x = 2 + \sqrt 3 t\\y = - 1 + 3t\end{array} \right.\) và \({\Delta _4}:\left\{ \begin{array}{l}x = 3 - \sqrt 3 t'\\y = - t'\end{array} \right.\)
c) \({\Delta _5}: - \sqrt 3 x + 3y + 2 = 0\) và \({\Delta _6}:\left\{ \begin{array}{l}x = 3t\\y = 1 - \sqrt 3 t\end{array} \right.\)
-
GiášĢi bà i 42 trang 82 SBT ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
TÃnh khoášĢng cÃĄch táŧŦ máŧt Äiáŧm Äášŋn máŧt ÄÆ°áŧng thášģng trong cÃĄc trÆ°áŧng háŧĢp sau:
a) A(â3 ; 1) và â1: 2x + y - 4 = 0
b) B(1; -3) và â2: \(\left\{ \begin{array}{l}x = - 3 + 3t\\y = 1 - t\end{array} \right.\)
-
GiášĢi bà i 43 trang 82 SBT ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
Cho hai ÄÆ°áŧng thášģng song song â1: ax + by + c = 0 và â2: ax + by + d = 0. CháŧĐng minh rášąng khoášĢng cÃĄch giáŧŊa hai ÄÆ°áŧng thášģng â1 và â2 bášąng \(\frac{{\left| {d - c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)
-
GiášĢi bà i 44 trang 82 SBT ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
Cho hai ÄÆ°áŧng thášģng â1: mx â 2y â 1 = 0 và â2: x - 2y + 3 = 0. Váŧi giÃĄ tráŧ nà o cáŧ§a tham sáŧ m thÃŽ:
a) â1 // â2?
b) â1\( \bot {\Delta _2}\)?
-
GiášĢi bà i 45 trang 82 SBT ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
Cho ba Äiáŧm A(-2; 2), B(4 ; 2), C(6 ; 4). Viášŋt phÆ°ÆĄng trÃŽnh ÄÆ°áŧng thášģng â Äi qua B Äáŧng tháŧi cÃĄch Äáŧu A và C.
-
GiášĢi bà i 46 trang 83 SBT ToÃĄn 10 CÃĄnh diáŧu tášp 2 - CD
CÃģ hai tà u Äiáŧn ngᚧm A và B chᚥy trong náŧi ÄÃī thà nh pháŧ cáŧ§ng xuášĨt phÃĄt táŧ hai ga, chuyáŧn Äáŧng Äáŧu theo ÄÆ°áŧng thášģng. TrÊn mà n hÃŽnh ra Äa cáŧ§a trᚥm Äiáŧu khiáŧn (ÄÆ°áŧĢc coi nhÆ° máš·t phášģng toᚥ Äáŧ Oxy váŧi ÄÆĄn váŧ trÊn cÃĄc tráŧĨc tÃnh theo ki-lÃī-mÃĐt), sau khi xuášĨt phÃĄt t (giáŧ) (t âĨ 0), váŧ trà cáŧ§a tà u A cÃģ toᚥ Äáŧ ÄÆ°áŧĢc xÃĄc Äáŧnh báŧi cÃīng tháŧĐc: \(\left\{ \begin{array}{l}x = 7 + 36t\\y = - 8 + 8t\end{array} \right.\) , váŧ trà cáŧ§a tà u B cÃģ toᚥ Äáŧ là (9 + 8t ; 5 â 36t).
a) TÃnh cÃīsin gÃģc giáŧŊa hai ÄÆ°áŧng Äi cáŧ§a hai tà u A và B
b) Sau bao lÃĒu káŧ táŧŦ tháŧi Äiáŧm xuášĨt phÃĄt hai tà u gᚧn nhau nhášĨt?