Trang chủ Toán 10

Bài tập 2 trang 49 SGK Đại số 10

Lý thuyết10 Trắc nghiệm

4 BT SGK

51 FAQ

Giải bài 2 tr 49 sách GK Toán ĐS lớp 10

Lập bảng biến thiên và vẽ đồ thị của các hàm số.

a) \(y = 3x^2- 4x + 1\);                      b) \(y = - 3x^2 + 2x - 1\);

c) \(y = 4x^2- 4x + 1\);                      d) \(y = - x^2 + 4x - 4\);

e) \(y = 2x^2+ x + 1\);                       f) \(y = - x^2 + x - 1\).

Hướng dẫn giải chi tiết bài 2

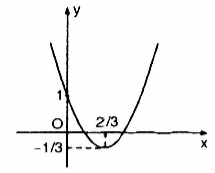
Câu a:

Hoành độ đỉnh \({x_0} =  - \frac{b}{{2a}} = \frac{2}{3} \Rightarrow {y_0} =  - \frac{1}{3}\)

Đỉnh \(I\left( {\frac{2}{3}; - \frac{1}{3}} \right)\)

Trục đối xứng: \(x = \frac{2}{3}\)

Giao điểm với Oy là A(0;1)

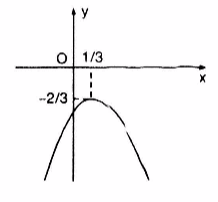
Câu b:

Đỉnh \(I\left( {\frac{1}{3}; - \frac{2}{3}} \right)\)

Trục đối xứng: \(x = \frac{1}{3}\)

Giao điểm với Oy là A(0;-1)

Bảng biến thiên và đồ thị

Câu c:

Đỉnh \(I\left( {\frac{1}{2};0} \right)\)

Trục đối xứng: \(x = \frac{1}{2}\)

Giao điểm với Oy là A(0;1)

Bảng biến thiên và đồ thị

Câu d:

Đỉnh \(I\left( {2;0} \right)\)

Trục đối xứng: \(x = 2\)

Giao điểm với Oy là A(0;-4)

Bảng biến thiên và đồ thị

Câu e:

Đỉnh \(I\left( { - \frac{1}{4};\frac{7}{8}} \right)\)

Trục đối xứng: \(x =  - \frac{1}{4}\)

Giao điểm với Oy là A(0;1)

Bảng biến thiên và đồ thị

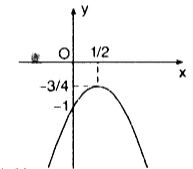
Câu f:

Đỉnh \(I\left( {\frac{1}{2}; - \frac{3}{4}} \right)\)

Trục đối xứng: \(x = \frac{1}{2}\)

Giao điểm với Oy là A(0;-1)

Bảng biến thiên và đồ thị

-- Mod Toán 10 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 2 trang 49 SGK Đại số 10 HAY thì click chia sẻ 

Để luyện tập thêm dạng bài tương tự như Bài tập 2 trang 49 trong SGK các em làm thêm câu hỏi trắc nghiệm sau để cũng cố kỹ năng làm dạng bài.

  • Câu 1:

    Hình vẽ bên là đồ thị của hàm số nào? 

    • A. \(y = - {\left( {x + 1} \right)^2}\)
    • B. \(y = - {\left( {x - 1} \right)^2}\)
    • C. \(y = {\left( {x + 1} \right)^2}\)
    • D. \(y = {\left( {x - 1} \right)^2}\)

Được đề xuất cho bạn