Giải bài 2.20 tr 41 SBT Toán 10
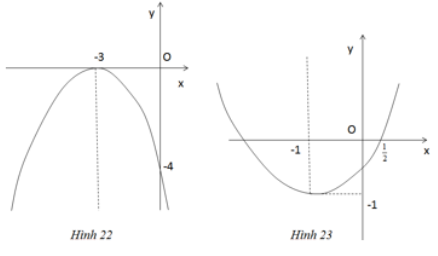
Viết phương trình của parabol y = ax2+bx+c ứng với mỗi đồ thị dưới đây
Hướng dẫn giải chi tiết
a) Dựa trên đồ thị (h.22) ta thấy parabol có đỉnh \(I( - 3;0)\) và đi qua điểm \((0; - 4)\)
Như vậy \(c = - 4; - \dfrac{b}{{2a}} = - 3 \Leftrightarrow b = 6a\).
Thay \(c = - 4\) và \(b = 6a\) vào biểu thức
\(\Delta = {b^2} - 4ac = 0\)\( = > 36{a^2} + 16a = 0 \) \(= > a = - \dfrac{4}{9}\) (vì \(a \ne 0)\) và \(b = - \dfrac{8}{3}\).
Vậy phương trình của parabol là \(y = - \dfrac{4}{9}{x^2} - \dfrac{8}{3}x - 4\).
b) Dựa trên đồ thị (h.23) ta thấy parabol có đỉnh \(I( - 1; - 1)\) và đi qua điểm \(\left( {\dfrac{1}{2};0} \right)\)
Như vậy \(\left\{ {\begin{array}{*{20}{c}}{\dfrac{1}{4}a + \dfrac{1}{2}b + c = 0}\\{ - \dfrac{b}{{2a}} = - 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{b = 2a}\\{c = - \dfrac{5}{4}a}\end{array}} \right.\).
Thay vào biểu thức \(\Delta = {b^2} - 4ac = - 1 \) \(= > 4{a^2} + 5a + 1 = 0 = > a = \dfrac{4}{9}\) (vì \(a > 0)\) \( \Rightarrow b = \dfrac{8}{9};c = \dfrac{{ - 5}}{9}\).
\(y = \dfrac{4}{9}{x^2} + \dfrac{8}{9}x - \dfrac{5}{9}\)
-- Mod Toán 10 HỌC247
-


A. R
B. \(\left[ {\frac{4}{3}; + \infty } \right]\)
C. \(\left( {\frac{4}{3}; + \infty } \right)\)
D. \(R\backslash \left[ {\frac{4}{3}; + \infty } \right)\)
Theo dõi (0) 1 Trả lời -


Tập xác định của hàm số \(y = f\left( x \right) = \;\sqrt {x - 3} - \sqrt {4 - x} \) là
bởi Trần Hoàng Mai
 24/05/2020
Theo dõi (0) 0 Trả lời
24/05/2020
Theo dõi (0) 0 Trả lời -


Cho parabol (P): y = \({x^2}\) – 2x + m – 1. Tìm tất cả các giá trị thực của tham số m để parabol (P) không cắt trục Ox.
bởi Lê Bảo An
 25/05/2020
Theo dõi (0) 1 Trả lời
25/05/2020
Theo dõi (0) 1 Trả lời -


Parabol (P): y = \({x^2}\) + 4x + 4 có số điểm chung với trục hoành là:
bởi Trần Bảo Việt
 25/05/2020
Theo dõi (0) 1 Trả lời
25/05/2020
Theo dõi (0) 1 Trả lời -


Gọi A(a; b) và B(c; d) là tọa độ giao điểm của (P): y = 2x – \({x^2}\) và (d): y = 3x – 6. Giá trị của b + d bằng
bởi Lê Bảo An
 24/05/2020
Theo dõi (0) 1 Trả lời
24/05/2020
Theo dõi (0) 1 Trả lời -


Tọa độ giao điểm của parabol (P): y = \({x^2}\)– 4x với đường thẳng (d): y = -x – 2 là:
bởi Nguyễn Lệ Diễm
 25/05/2020
25/05/2020
A. M(-1; -1) và N(-2; 0).
B. M(1; -3) và N(2; -4).
C. M(0; -2) và N(2; -4).
D. M(-3; 1) và N(3; -5).
Theo dõi (0) 1 Trả lời -


Tìm parabol (P): y = a\({x^2}\) + 3x – 2 biết rằng có trục đối xứng x = -3.
bởi Trịnh Lan Trinh
 25/05/2020
Theo dõi (0) 1 Trả lời
25/05/2020
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 2.18 trang 41 SBT Toán 10
Bài tập 2.19 trang 41 SBT Toán 10
Bài tập 2.21 trang 42 SBT Toán 10
Bài tập 2.22 trang 42 SBT Toán 10
Bài tập 2.23 trang 42 SBT Toán 10
Bài tập 2.24 trang 42 SBT Toán 10
Bài tập 2.25 trang 42 SBT Toán 10
Bài tập 2.26 trang 42 SBT Toán 10
Bài tập 27 trang 58 SGK Toán 10 NC
Bài tập 28 trang 59 SGK Toán 10 NC
Bài tập 29 trang 59 SGK Toán 10 NC
Bài tập 30 trang 59 SGK Toán 10 NC
Bài tập 31 trang 59 SGK Toán 10 NC
Bài tập 32 trang 59 SGK Toán 10 NC
Bài tập 33 trang 60 SGK Toán 10 NC
Bài tập 34 trang 60 SGK Toán 10 NC
Bài tập 35 trang 60 SGK Toán 10 NC
Bài tập 36 trang 60 SGK Toán 10 NC