Giải bài 2.19 tr 41 SBT Đại số 10
Lập bảng biến thiên và vẽ đồ thị của hàm số bậc hai
a) y = 2x2+4x−6;
b) y = −3x2−6x+4;
c) \(y = \sqrt 3 {x^2} + 2\sqrt 3 x + 2\);
d) y = −2(x2+1).
Hướng dẫn giải chi tiết
a) Hàm số bậc hai đã cho có a = 2; b = 4;c = −6
Vậy \( - \frac{b}{{2a}} = - 1;\Delta = {b^2} - 4ac = 64; - \frac{\Delta }{{4a}} = - 8\)
Vì a > 0, ta có bảng biến thiên
Hàm số nghịch biến trên khoảng (−∞;−1), đồng biến trên khoảng (−1;+∞).
Để vẽ đồ thị ta có trục đối xứng là đường thẳng x = −1; đỉnh I(−1;−8); giao với tục tung tại điểm (0;−6); giao với trục hoành tại các điểm (−3;0) và (1;0).
Đồ thị của hàm số y = 2x2+4x−6 được vẽ trên hình
.jpg)
b)
Hàm số bậc hai đã cho có a = −3; b = −6; c = 4
Vậy \( - \frac{b}{{2a}} = - 1,\Delta = {b^2} - 4ac = 84, - \frac{\Delta }{{4a}} = 7\)
Vì a < 0, ta có bảng biến thiên
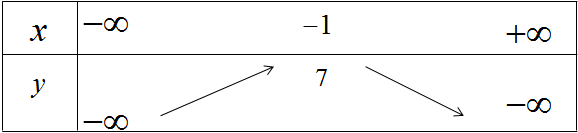
Hàm số đồng biến trên khoảng (−∞;−1) và nghịch biến trên khoảng (−1;+∞).
Để vẽ đồ thị ta có trục đối xứng là đường thẳng x = −1; đỉnh I(−1;7) giao với tục tung tại điểm (0;4)
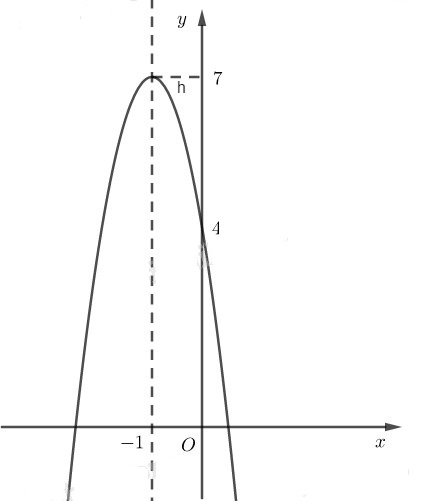
c) Hàm số bậc hai đã cho có \(a = \sqrt 3 ;b = 2\sqrt 3 ,c = 2\)
Vậy \( - \frac{b}{{2a}} = - 1,\Delta = {b^2} - 4ac = 12 - 8\sqrt 3 , - \frac{\Delta }{{4a}} = 2 - \sqrt 3 \)
Vì a > 0, ta có bảng biến thiên
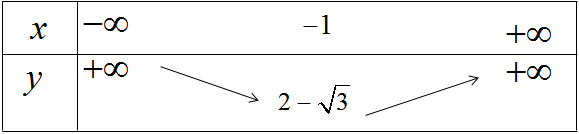
Hàm số nghịch biến trên khoảng (−∞;−1) và đồng biến trên khoảng (−1;+∞).
Để vẽ đồ thị ta có trục đối xứng là đường thẳng x = −1; đỉnh \(I\left( { - 1;2 - \sqrt 3 } \right)\) giao với tục tung tại điểm (0;2)
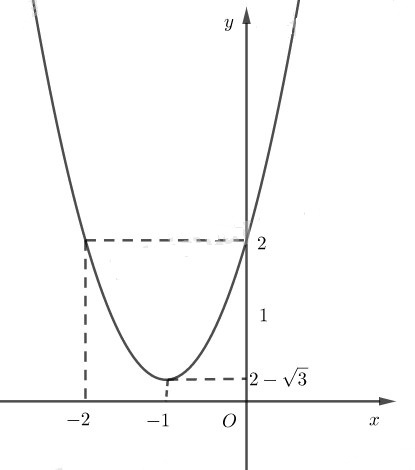
-- Mod Toán 10 HỌC247
-


Xác định parabol (P): y = a\({x^2}\) + bx + c biết rằng parabol (P) đi qua ba điểm A(1; 1), B(-1; -3) và O(0; 0).
bởi Trần Bảo Việt
 25/05/2020
25/05/2020
A. y = x2 + 2x.
B. y = -x2 – 2x.
C. y = -x2 + 2x.
D. y = x2 – 2x.
Theo dõi (0) 1 Trả lời -


Tìm tập xác định D của hàm số \(y = \frac{{x + 4}}{{\sqrt {{x^2} - 16} }}\)
bởi Nguyễn Sơn Ca
 25/05/2020
Theo dõi (0) 1 Trả lời
25/05/2020
Theo dõi (0) 1 Trả lời -


Tìm tập xác định D của hàm số \(y = \;\sqrt {x + 2} - \sqrt {x + 3} \)
bởi Nguyễn Lệ Diễm
 24/05/2020
Theo dõi (0) 2 Trả lời
24/05/2020
Theo dõi (0) 2 Trả lời -


Tìm tập xác định D của hàm số \(y = \frac{{{x^2} + 1}}{{{x^2} + 3x - 4}}\)
bởi Trần Hoàng Mai
 25/05/2020
Theo dõi (0) 2 Trả lời
25/05/2020
Theo dõi (0) 2 Trả lời -


Hình vẽ bên là đồ thị của hàm số nào dưới đây?
bởi Trần Hoàng Mai
 25/05/2020
25/05/2020
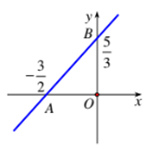
A. y = 10x + 15.
B. y = 10x + 5.
C. \(y = \frac{{10x}}{9} + \frac{5}{3}\)
D. \(y = \frac{{10x}}{9} + \frac{5}{9}\)
Theo dõi (0) 1 Trả lời -


Hình vẽ bên là đồ thị của hàm số nào?
bởi Nguyễn Thanh Trà
 25/05/2020
25/05/2020
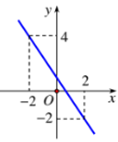
A. \(y = - \frac{{3x}}{2} + 1\)
B. y = -3x + 2.
C. \(y = - \frac{{3x}}{2} - 1\)
D. y = 3x + 2.
Theo dõi (0) 1 Trả lời -


Miền giá trị của hàm số y = 2\({x^2}\)– 6 là:
bởi Trịnh Lan Trinh
 25/05/2020
Theo dõi (0) 1 Trả lời
25/05/2020
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 4 trang 50 SGK Đại số 10
Bài tập 2.18 trang 41 SBT Toán 10
Bài tập 2.20 trang 41 SBT Toán 10
Bài tập 2.21 trang 42 SBT Toán 10
Bài tập 2.22 trang 42 SBT Toán 10
Bài tập 2.23 trang 42 SBT Toán 10
Bài tập 2.24 trang 42 SBT Toán 10
Bài tập 2.25 trang 42 SBT Toán 10
Bài tập 2.26 trang 42 SBT Toán 10
Bài tập 27 trang 58 SGK Toán 10 NC
Bài tập 28 trang 59 SGK Toán 10 NC
Bài tập 29 trang 59 SGK Toán 10 NC
Bài tập 30 trang 59 SGK Toán 10 NC
Bài tập 31 trang 59 SGK Toán 10 NC
Bài tập 32 trang 59 SGK Toán 10 NC
Bài tập 33 trang 60 SGK Toán 10 NC
Bài tập 34 trang 60 SGK Toán 10 NC
Bài tập 35 trang 60 SGK Toán 10 NC
Bài tập 36 trang 60 SGK Toán 10 NC




.PNG)

