Bài tập 18 trang 200 SGK Toán 10 NC
Tính giá trị lượng giác của góc α trong mỗi trường hợp sau:
a) \(\cos \alpha = \frac{1}{4};\sin \alpha < 0\)
b) \(\sin \alpha = - \frac{1}{3};\frac{\pi }{2} < \alpha < \frac{{3\pi }}{2}\)
c) \(\tan \alpha = \frac{1}{2}; - \pi < \alpha < 0\)
Hướng dẫn giải chi tiết
a) Ta có
\(\begin{array}{l}
\sin \alpha = - \sqrt {1 - c{\rm{o}}{{\rm{s}}^2}\alpha } \\
= - \sqrt {1 - \frac{1}{{16}}} = - \frac{{\sqrt {15} }}{4}\left( {do{\mkern 1mu} \sin \alpha < 0} \right)
\end{array}\)
\(\begin{array}{l}
\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = - \sqrt {15} \\
\cot \alpha = \frac{1}{{\tan \alpha }} = - \frac{{\sqrt {15} }}{{15}}
\end{array}\)
b) Vì \(\frac{\pi }{2} < \alpha < \frac{{3\pi }}{2} \)
\(\Rightarrow \cos \alpha = - \sqrt {1 - {{\sin }^2}\alpha } = - \frac{{2\sqrt 2 }}{3}\)
\(\begin{array}{l}
\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{1}{{2\sqrt 2 }} = \frac{{\sqrt 2 }}{4}\\
\cot \alpha = \frac{1}{{\tan \alpha }} = 2\sqrt 2
\end{array}\)
c)
Vì \(\left\{ \begin{array}{l}
- \pi < \alpha < 0\\
\tan \alpha = \frac{1}{2}
\end{array} \right. \Rightarrow \cos \alpha < 0\)
\(\begin{array}{l}
\Rightarrow \cos \alpha = - \frac{1}{{\sqrt {1 + {{\tan }^2}\alpha } }} = - \frac{{2\sqrt 2 }}{5}\\
\sin \alpha = \tan \alpha .\cot \alpha = - \frac{{\sqrt 5 }}{5}\\
\cot \alpha = \frac{1}{{\tan \alpha }} = 2
\end{array}\)
-- Mod Toán 10 HỌC247
-


Tính sin^3a-cos^3a biết sin a- cos a =m
bởi Huỳnh Như
 27/04/2020
27/04/2020
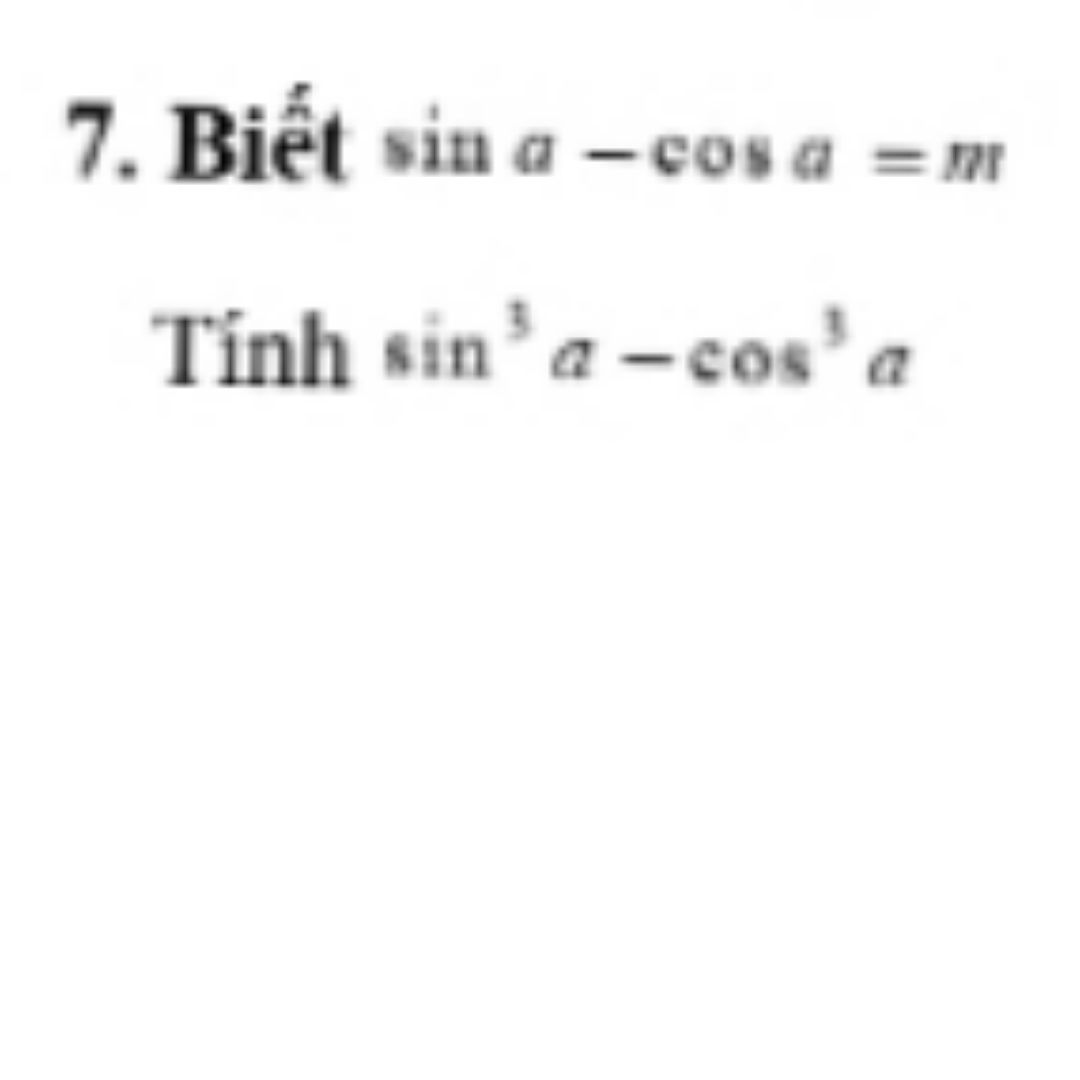 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Chứng minh sin(9pi/2+anpha)=cos anpha
bởi Milkmlik
 24/04/2020
24/04/2020
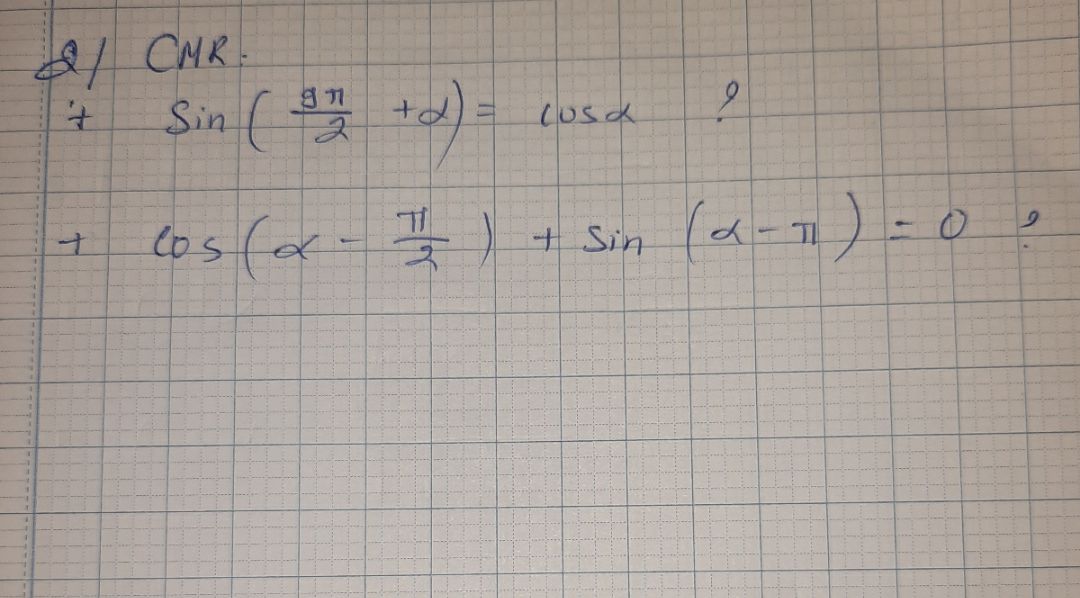 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Chứng minh tan ^2x - cot^2x /sin^2x độc lập với x
bởi Khánh Ngọc
 24/04/2020
chứng minh tan ^2x - cot^2x /sin^2x độc lập với xTheo dõi (0) 0 Trả lời
24/04/2020
chứng minh tan ^2x - cot^2x /sin^2x độc lập với xTheo dõi (0) 0 Trả lời -


Xác định giá trị dấu của sin 177°
bởi yên chi
 14/04/2020
Xác định giá trị dấu của sin 177°Theo dõi (0) 4 Trả lời
14/04/2020
Xác định giá trị dấu của sin 177°Theo dõi (0) 4 Trả lời
Bài tập SGK khác
Bài tập 16 trang 200 SGK Toán 10 NC
Bài tập 17 trang 200 SGK Toán 10 NC
Bài tập 19 trang 200 SGK Toán 10 NC
Bài tập 20 trang 201 SGK Toán 10 NC
Bài tập 21 trang 201 SGK Toán 10 NC
Bài tập 22 trang 201 SGK Toán 10 NC
Bài tập 23 trang 201 SGK Toán 10 NC
Bài tập 24 trang 205 SGK Toán 10 NC
Bài tập 25 trang 205 SGK Toán 10 NC
Bài tập 26 trang 205 SGK Toán 10 NC
Bài tập 27 trang 206 SGK Toán 10 NC
Bài tập 28 trang 206 SGK Toán 10 NC
Bài tập 30 trang 206 SGK Toán 10 NC
Bài tập 31 trang 206 SGK Toán 10 NC
Bài tập 32 trang 206 SGK Toán 10 NC
Bài tập 33 trang 206 SGK Toán 10 NC
Bài tập 34 trang 207 SGK Toán 10 NC
Bài tập 35 trang 207 SGK Toán 10 NC





