Câu hỏi trắc nghiệm (50 câu):
-
Câu 1: Mã câu hỏi: 260392
Từ một nhóm có 10 học sinh. Có bao nhiêu cách chọn ra 3 học sinh và xếp thành một hàng ngang?
- A. 10!
- B. \(A_{10}^3.\)
- C. \(10C_{10}^3.\)
- D. 103
-
Câu 2: Mã câu hỏi: 260397
Cho cấp số cộng \(\left( {{u}_{n}} \right)\) có \({{u}_{5}}=6\) và công sai d=1. Giá trị của \({{u}_{3}}\) bằng
- A. 6
- B. 9
- C. 4
- D. 5
-
Câu 3: Mã câu hỏi: 260401
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào, trong các khoảng dưới đây?
- A. \(\left( { - \infty ; - 2} \right).\)
- B. \(\left( { - \infty ;0} \right).\)
- C. (-1;1)
- D. \(\left( { - 1; + \infty } \right).\)
-
Câu 4: Mã câu hỏi: 260414
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
Điểm cực đại của đồ thị hàm số đã cho là
- A. x = 3
- B. (-1;3)
- C. x = 2
- D. (2;1)
-
Câu 5: Mã câu hỏi: 260427
Cho hàm số \(f\left( x \right)\) có bảng xét dấu của đạo hàm \({f}'\left( x \right)\) như sau:
.png)
Hàm số \(f\left( x \right)\) có bao nhiêu điểm cực trị?
- A. 4
- B. 1
- C. 3
- D. 2
-
Câu 6: Mã câu hỏi: 260433
Tiệm cận đứng của đồ thị hàm số \(y=\frac{-2x+4}{-x+1}\) là đường thẳng:
- A. x = 1
- B. x = -1
- C. x = 2
- D. x = -2
-
Câu 7: Mã câu hỏi: 260442
Hàm số \(y={{x}^{4}}-1\) có đồ thị là hình nào dưới đây?
- A. Hình 1.
- B. Hình 2.
- C. Hình 3.
- D. Hình 4.
-
Câu 8: Mã câu hỏi: 260453
Đồ thị của hàm số \(y = {\left( {x - 1} \right)^2}\left( {x + 2} \right)\) cắt trục tung tại điểm có tung độ bằng
- A. 4
- B. 2
- C. -2
- D. 0
-
Câu 9: Mã câu hỏi: 260455
Với a là số thực dương tùy ý, \(\ln \left( {ea} \right)\) bằng
- A. \(1 + \ln a.\)
- B. lna
- C. \(\frac{1}{{\ln a}}.\)
- D. \({\log _a}e.\)
-
Câu 10: Mã câu hỏi: 260459
Đạo hàm của hàm số \(y = {\pi ^x}\) là
- A. \(y' = x{\pi ^{x - 1}}.\)
- B. \(y' = \frac{{{\pi ^x}}}{{\ln \pi }}.\)
- C. \(y' = {\pi ^x}\ln \pi .\)
- D. \(y' = {\pi ^x}.\)
-
Câu 11: Mã câu hỏi: 260462
Với a là số thực dương tùy ý, \(a\sqrt[3]{a}\) bằng
- A. \({a^{\frac{3}{2}}}.\)
- B. \({a^{\frac{3}{4}}}.\)
- C. \({a^{\frac{2}{3}}}.\)
- D. \({a^{\frac{4}{3}}}.\)
-
Câu 12: Mã câu hỏi: 260465
Nghiệm của phương trình \({4^{2x - 1}} = 32\) là
- A. x = 5
- B. \(x = \frac{7}{4}.\)
- C. \(x = \frac{9}{4}.\)
- D. \(x = - \frac{9}{4}.\)
-
Câu 13: Mã câu hỏi: 260468
Nghiệm của phương trình \({{\log }_{3}}\left( 1-3x \right)=2\) là
- A. \(x = - \frac{8}{3}.\)
- B. \(x = \frac{2}{3}.\)
- C. \(x = \frac{8}{3}.\)
- D. \(x = - \frac{3}{2}.\)
-
Câu 14: Mã câu hỏi: 260472
Cho hàm số \(f\left( x \right)=-3{{x}^{2}}+1.\) Trong các khẳng định sau, khẳng định nào đúng?
- A. \(\int {f\left( x \right){\rm{d}}x = 3{x^3} - x + C.} \)
- B. \(\int {f\left( x \right){\rm{d}}x = - {x^3} + x - C.} \)
- C. \(\int {f\left( x \right){\rm{d}}x = \frac{1}{3}{x^3} + x + C.} \)
- D. \(\int {f\left( x \right){\rm{d}}x = - 3{x^3} - C.} \)
-
Câu 15: Mã câu hỏi: 260479
Hàm \(F\left( x \right)=\cos 2x+5\) là một nguyên hàm của hàm số nào dưới đây?
- A. \(f\left( x \right) = - 2\sin x\)
- B. \(f\left( x \right) = - \frac{1}{2}\sin 2x\)
- C. \(f\left( x \right) = 2\sin x\)
- D. \(f\left( x \right) = - 2\sin 2x\)
-
Câu 16: Mã câu hỏi: 260698
Nếu \(\int\limits_{1}^{2}{f\left( x \right)dx=-2}\) và \(\int\limits_{1}^{3}{f\left( x \right)dx=6}\) thì \(\int\limits_{2}^{3}{f\left( x \right)dx}\) bằng
- A. 8
- B. 4
- C. -8
- D. 0
-
Câu 17: Mã câu hỏi: 260699
Tích phân \(\int\limits_0^1 {\left( {{x^2} + x} \right)dx} \) bằng
- A. 3
- B. \(\frac{5}{6}\)
- C. \(\frac{6}{5}\)
- D. 2
-
Câu 18: Mã câu hỏi: 260700
Số phức liên hợp của số phức z = 2021i là
- A. \(\overline z = 20 - 21i\)
- B. \(\overline z = 2021 + i\)
- C. \(\overline z = 2021 - i\)
- D. \(\overline z = - 2021i\)
-
Câu 19: Mã câu hỏi: 260702
Cho số phức z=2-3i và \(\text{w}=1+i\). Số phức \(z+2\text{w}\) bằng
- A. 4 - i
- B. 4 + i
- C. -4 + i
- D. -1 + 4i
-
Câu 20: Mã câu hỏi: 260704
Trên mặt phẳng tọa độ, điểm \(M\left( 2;-3 \right)\) biểu diễn số phức nào dưới đây?
- A. z = - 2 + 3i
- B. z = 2 + 3i
- C. z = 2 - 3i
- D. z = - 3 + 2i
-
Câu 21: Mã câu hỏi: 260707
Cho khối chóp S.ABCD có đáy là hình vuông cạnh đáy bằng a và SA vuông góc với đáy với \(SA=a\sqrt{3}.\) Thể tích của khối chóp S.ABCD bằng
- A. \(3{a^3}\)
- B. \({a^3}\sqrt 3 \)
- C. \(\frac{{{a^3}}}{3}\)
- D. \(\frac{{{a^3}\sqrt 3 }}{3}\)
-
Câu 22: Mã câu hỏi: 260711
Thể tích khối lập phương có cạnh 3a là
- A. \(\frac{{{a^3}}}{{27}}\)
- B. \(\frac{{{a^3}}}{3}\)
- C. \({a^3}\)
- D. \(27{a^3}\)
-
Câu 23: Mã câu hỏi: 260715
Công thức tính thể tích \(V\) của khối trụ có bán kính đáy r và chiều cao h là
- A. \(V = \pi rh\)
- B. \(V = \pi {r^2}h\)
- C. \(V = \frac{1}{3}\pi rh\)
- D. \(V = \frac{1}{3}\pi {r^2}h\)
-
Câu 24: Mã câu hỏi: 260721
Cho hình trụ có bán kính đáy bằng 3cm, độ dài đường cao bằng 4cm. Diện tích xung quanh của hình trụ bằng
.png)
- A. \(26\pi \,{\rm{c}}{{\rm{m}}^2}\)
- B. \(22\pi {\rm{ c}}{{\rm{m}}^2}\)
- C. \(24\pi {\rm{ c}}{{\rm{m}}^2}\)
- D. \(20\pi \,{\rm{c}}{{\rm{m}}^2}\)
-
Câu 25: Mã câu hỏi: 260727
Trong không gian Oxyz, cho hai điểm \(A\left( 1;2;4 \right)\) và \(B\left( 2;4;-1 \right)\). Tìm tọa độ trọng tâm G của tam giác OAB.
- A. G(2;1;1)
- B. G(6;3;3)
- C. G(2;1;1)
- D. G(1;2;1)
-
Câu 26: Mã câu hỏi: 260733
Trong không gian Oxyz, cho mặt cầu \(\left( S \right):{{\left( x+1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z-1 \right)}^{2}}=9\). Tìm tọa độ tâm I của mặt cầu \(\left( S \right)\).
- A. \(I\left( {1; - 2; - 1} \right)\)
- B. \(I\left( { - 1; - 2; - 1} \right)\)
- C. \(I\left( {1;2;1} \right)\)
- D. \(I\left( { - 1;2;1} \right)\)
-
Câu 27: Mã câu hỏi: 260739
Trong không gian Oxyz, cho điểm \(M\left( m;1;6 \right)\) và mặt phẳng \(\left( P \right):x-2y+z-5=0\). Điểm M thuộc mặt phẳng \(\left( P \right)\) khi giá trị của tham số m là
- A. m = -1
- B. m = 3
- C. m = -3
- D. m = 1
-
Câu 28: Mã câu hỏi: 260746
Trong không gian Oxyz, một véctơ chỉ phương của đường thẳng \(d:\frac{x-2}{-1}=\frac{y-1}{2}=\frac{z}{1}\) là
- A. \(\vec u = \left( {2;1;0} \right)\)
- B. \(\vec u = \left( { - 1;2;1} \right)\)
- C. \(\vec u = \left( { - 1;2;0} \right)\)
- D. \(\vec u = \left( {2;1;1} \right)\)
-
Câu 29: Mã câu hỏi: 260750
Gọi S là tập các số tự nhiên có bốn chữ số khác nhau được tạo từ tập \(E=\left\{ 1;2;3;4;5 \right\}\). Chọn ngẫu nhiên một số từ tập S. Tính xác suất để số được chọn là một số lẻ.
- A. \(\frac{1}{2}\)
- B. \(\frac{3}{4}\)
- C. \(\frac{3}{5}\)
- D. \(\frac{2}{5}\)
-
Câu 30: Mã câu hỏi: 260755
Hàm số nào sau đây đồng biến trên tập xác định của nó?
- A. \(y = {\left( {\frac{1}{3}} \right)^x}\)
- B. \(y = {{\rm{e}}^{ - x}}\)
- C. \(y = {\log _{\frac{1}{5}}}x\)
- D. \(y = \ln x\)
-
Câu 31: Mã câu hỏi: 260761
Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right)=\frac{x+3}{x-1}\) trên đoạn \(\left[ 2;3 \right]\) lần lượt là M và m. Tổng M+m bằng
- A. -1
- B. 0
- C. 5
- D. 8
-
Câu 32: Mã câu hỏi: 260768
Tập nghiệm của bất phương trình \({\left( {\frac{1}{2}} \right)^{{x^2} - x}} > {2^{x - 4}}\) là
- A. \(S = ( - 2; + \infty )\)
- B. \(S = (2; + \infty )\)
- C. \(S = ( - \infty ; - 2) \cup (2; + \infty )\)
- D. \(S = ( - 2;2)\)
-
Câu 33: Mã câu hỏi: 260774
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và \(\int\limits_{0}^{1}{\left[ f\left( x \right)+3{{x}^{2}} \right]\text{d}x}=6\). Khi đó \(\int\limits_{0}^{1}{f\left( x \right)\text{d}x}\) bằng
- A. 0
- B. 5
- C. 3
- D. 9
-
Câu 34: Mã câu hỏi: 260780
Cho số phức z=2+3i. Tìm môđun của số phức \(w=\left( 1+i \right)z-\bar{z}\)
- A. 5
- B. 8
- C. \(\sqrt {63} \)
- D. \(\sqrt 7 \)
-
Câu 35: Mã câu hỏi: 260791
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng \(\left( ABC \right)\) và \(SA=a\sqrt{2}\), biết tam giác ABC vuông cân tại B và AC=2a (minh họa như hình vẽ).
.png)
Tính số đo góc giữa đường thẳng SB và mặt phẳng (ABC).
- A. 90o
- B. 30o
- C. 60o
- D. 45o
-
Câu 36: Mã câu hỏi: 260798
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B với AB=BC=a, AD=2a. Biết \(SA\bot \left( ABCD \right)\) và SA=a. Tính khoảng cách giữa AD và SB.
- A. \(\frac{{a\sqrt 2 }}{4}\)
- B. \(\frac{a}{2}\)
- C. \(\frac{{a\sqrt 3 }}{3}\)
- D. \(\frac{{a\sqrt 2 }}{2}\)
-
Câu 37: Mã câu hỏi: 260805
Trong không gian Oxyz, cho hai điểm \(A\left( 2;1;1 \right), B\left( 0;3;-1 \right)\). Mặt cầu \(\left( S \right)\) đường kính AB có phương trình là
- A. \({x^2} + {\left( {y - 2} \right)^2} + {z^2} = 3\)
- B. \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {z^2} = 9\)
- C. \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 9\)
- D. \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {z^2} = 3\)
-
Câu 38: Mã câu hỏi: 260815
Trong không gian Oxyz, cho tam giác ABC với \(A\left( 3;1;2 \right), B\left( -3;2;5 \right), C\left( 1;6;-3 \right)\). Khi đó phương trình trung tuyến AM của tam giác ABC là
- A. \(\left\{ \begin{array}{l} x = 1 + t\\ y = - 1 - 3t\\ z = 8 - 4t \end{array} \right.\)
- B. \(\left\{ \begin{array}{l} x = 3 - 4t\\ y = 1 + 3t\\ z = 2 - t \end{array} \right.\)
- C. \(\left\{ \begin{array}{l} x = 1 - 4t\\ y = - 3 + 3t\\ z = 4 - 1t \end{array} \right.\)
- D. \(\left\{ \begin{array}{l} x = 1 + 3t\\ y = - 3 + 4t\\ z = 4 - t \end{array} \right.\)
-
Câu 39: Mã câu hỏi: 260831
Cho \(y=f\left( x \right)\) có đồ thị của \(y={f}'\left( x \right)\) như hình vẽ dưới đây.
Đặt \(M=\underset{\left[ \text{-2;6} \right]}{\mathop{\text{max}}}\,\text{ }f\left( x \right), m=\underset{\left[ \text{-2;6} \right]}{\mathop{\text{min}}}\,\text{ }f\left( x \right)\). Giá trị của biểu thức M+m bằng
- A. f(0) + f(2)
- B. f(5) + f(-2)
- C. f(5) + f(6)
- D. f(0) - f(2)
-
Câu 40: Mã câu hỏi: 260842
Số giá trị nguyên dương của tham số m thỏa m<10 để bất phương trình \({{3}^{2x+2}}-{{3}^{x}}.({{3}^{m+2}}+1)+{{3}^{m}}<0\) có ít nhất 3 nghiệm nguyên là
- A. 6
- B. 9
- C. 5
- D. 8
-
Câu 41: Mã câu hỏi: 260847
Giả sử hàm số f liên tục trên đoạn [0;2] thỏa mãn \(\int\limits_{0}^{1}{f(x)\text{dx}}=6, \int\limits_{1}^{2}{f(x)\text{dx}}=-2\). Giá trị của tích phân \(\int\limits_{0}^{{\pi }/{2}\;}{f(2\sin x)\cos x\text{dx}}\) là
- A. -8
- B. 8
- C. 4
- D. 2
-
Câu 42: Mã câu hỏi: 260853
Cho số phức \(z=a+bi\text{ }\left( a,b\in \mathbb{R} \right)\) thỏa mãn \(\left| z \right|=5\) và \(z\left( 2+i \right)\left( 1-2i \right)\) là một số thực. Tính giá trị của \(P=\left| a \right|+\left| b \right|\).
- A. P = 8
- B. P = 4
- C. P = 5
- D. P = 7
-
Câu 43: Mã câu hỏi: 260869
Cho hình chóp S.ABC có ABC là tam giác đều và cạnh bên SA vuông góc với đáy, với \(SA=\frac{a}{2}\). Góc tạo bởi mặt phẳng \(\left( SBC \right)\) và mặt phẳng \(\left( ABC \right)\) bằng \(30{}^\circ \). Thể tích của khối chóp S.ABC bằng
- A. \(\frac{{{a^3}\sqrt 3 }}{8}\)
- B. \(\frac{{{a^3}\sqrt 3 }}{{24}}\)
- C. \(\frac{{{a^3}}}{4}\)
- D. \(\frac{{{a^3}}}{{12}}\)
-
Câu 44: Mã câu hỏi: 260877
Nghiêng một cốc nước hình trụ có đựng nước, người ta thấy bề mặt nước là hình elip có độ dài trục lớn là \(10\,\text{ cm}\), khoảng cách từ hai đỉnh trên trục lớn của elip đến đáy cốc lần lượt là \(5\text{ cm}\) và \(11\,\text{ cm}\). Tính thể tích nước trong cốc.
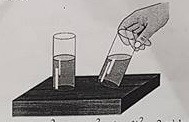
- A. \(96\pi \,{\rm{c}}{{\rm{m}}^{\rm{3}}}\)
- B. \(100\pi {\rm{ c}}{{\rm{m}}^{\rm{3}}}\)
- C. \(128\pi {\rm{ c}}{{\rm{m}}^{\rm{3}}}\)
- D. \(172\pi \,{\rm{c}}{{\rm{m}}^{\rm{3}}}\)
-
Câu 45: Mã câu hỏi: 260890
Trong không gian Oxyz cho đường thẳng \(\Delta :\frac{x}{1}=\frac{y+1}{2}=\frac{z-1}{1}\) và mặt phẳng \(\left( P \right):x-2y-z+3=0\). Đường thẳng nằm trong \(\left( P \right)\) đồng thời cắt và vuông góc với \(\Delta \) có phương trình là
- A. \(\left\{ \begin{array}{l} x = 1 + 2t\\ y = 1 - t\\ z = 2 \end{array} \right.\)
- B. \(\left\{ \begin{array}{l} x = - 3\\ y = - t\\ z = 2t \end{array} \right.\)
- C. \(\left\{ \begin{array}{l} x = 1 + t\\ y = 1 - 2t\\ z = 2 + 3t \end{array} \right.\)
- D. \(\left\{ \begin{array}{l} x = 1\\ y = 1 - t\\ z = 2 + 2t \end{array} \right.\)
-
Câu 46: Mã câu hỏi: 260906
Cho f(x) là hàm số bậc bốn thỏa mãn f(0)=0. Hàm số \({{f}^{\prime }}(x)\) có bảng biến thiên như sau:
Hàmsố \(g(x)=\left| f\left( {{x}^{3}} \right)-2021x \right|\) có bao nhiêu điểm cực trị?
- A. 3
- B. 5
- C. 4
- D. 2
-
Câu 47: Mã câu hỏi: 260911
Có bao nhiêu số nguyên y để tồn tại số thực x thỏa mãn \({\log _3}\left( {x + 2y} \right) = {\log _2}\left( {{x^2} + {y^2}} \right)\)
- A. 3
- B. 2
- C. 1
- D. Vô số
-
Câu 48: Mã câu hỏi: 260924
Cho hàm số \(y={{x}^{4}}-3{{x}^{2}}+m\) có đồ thị \(\left( {{C}_{m}} \right)\),với m là tham số thực.Giả sử \(\left( {{C}_{m}} \right)\) cắt trục Ox tại bốn điểm phân biệt như hình vẽ
Gọi \({{S}_{1}},{{S}_{2}},{{S}_{3}}\) là diện tích các miền gạch chéo được cho trên hình vẽ. Giá trị của m để \({{S}_{1}}+{{S}_{3}}={{S}_{2}}\) là
- A. \(\frac{5}{2}\)
- B. \(\frac{-5}{2}\)
- C. \(\frac{5}{4}\)
- D. \(\frac{-5}{4}\)
-
Câu 49: Mã câu hỏi: 260936
Cho hai số phức \({{z}_{1}},{{z}_{2}}\) thỏa mãn \(\left| {{z}_{1}}-5+3i \right|=\left| {{z}_{1}}-1-3i \right|,\left| {{z}_{2}}-4-3i \right|=\left| {{z}_{2}}-2+3i \right|\). Giá trị nhỏ nhất của biểu thức \(P=\left| {{z}_{1}}-{{z}_{2}} \right|+\left| \overline{{{z}_{1}}}-6+i \right|+\left| {{z}_{2}}-6-i \right|\) là
- A. \(2\sqrt {10} .\)
- B. 6
- C. \(\frac{{16}}{{\sqrt {13} }}.\)
- D. \(\frac{{18}}{{\sqrt {13} }}.\)
-
Câu 50: Mã câu hỏi: 260955
Trong không gian với hệ tọa độ Oxyz,cho mặt phẳng \(\left( P \right):x+y+z-1=0\), đường thẳng \(\left( d \right):\frac{x-15}{1}=\frac{y-22}{2}=\frac{z-37}{2}\) và mặt cầu \(\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-8x-6y+4z+4=0\).Một đường thẳng \(\left( \Delta \right)\) thay đổi cắt mặt cầu \(\left( S \right)\) tại hai điểm A,B sao cho AB=8. Gọi \({A}', {B}'\) là hai điểm lần lượt thuộc mặt phẳng \(\left( P \right)\) sao cho \(A{A}',B{B}'\) cùng song song với \(\left( d \right)\).Giá trị lớn nhất của biểu thức \(A{A}'+B{B}'\) là
- A. \(\frac{{24 + 18\sqrt 3 }}{5}\)
- B. \(\frac{{12 + 9\sqrt 3 }}{5}\)
- C. \(\frac{{16 + 60\sqrt 3 }}{9}\)
- D. \(\frac{{8 + 30\sqrt 3 }}{9}\)


.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)




