Tính thể tích tứ diện ABCD có diện tích tam giác ABC =4cm^2

nguyên hàm của x^2/căn(x^2+4)

điền 2 số còn thiếu vào dãy số

5 16 36 72 120 180 ... ... 

ai giải giúp mình và giải thích cách giải với ạ

A. 4x-2y-3z-11=0

B. - 4x+2y-3z+11=0

C. 4x-2y+3z+11=0

D. 4x+2y+3z+11=0

Mọi người giúp mình với!!!

Trong không gian với hệ tọa độ Oxyz, cho điểm M (2; -1; -6) và hai đường thẳng \(d_1: \dfrac{ x−1}{2}=\dfrac{ y−1}{−1}=\dfrac{ z+1}{1}\) , \(d_2: \dfrac{ x+2}{3}=\dfrac{ y+1}{1}=\dfrac{ z-2}{2}\). Đường thẳng đi qua điểm M và cắt cả hai đường thẳng \(d_1, d_2\) ${}_{}$tại hai điểm A, B. Độ dài đoạn thẳng AB bằng

A. \(\sqrt{38}\)

B. \(2\sqrt{10}\)

C. 8.

D. 12.

1. Lập phương trình đoạn thẳng d đi qua M(-3::1), N(0;1;3) và song song d2 có ptts x=3+2t: y=-t: z=-1+3t

Trong không gian với hệ tọa độ \(\text{O}xyz\), cho các điểm \(A\left( 1;0;0 \right)\), \(B\left( 0;2;0 \right)\), \(C\left( 0;0;4 \right)\).Viết phương trình đường thẳng \(\Delta \) đi qua trực tâm \(H\) của tam giác \(\Delta ABC\) và vuông góc với mặt phẳng \(\left( ABC \right)\).

A. \(\Delta :\,\frac{x-1}{-4}=\frac{y}{2}=\frac{z}{1}\).                            B. \(\Delta :\,\frac{x-1}{4}=\frac{y-1}{2}=\frac{z}{-1}\).

C. \(\Delta :\,\frac{x}{4}=\frac{y}{2}=\frac{z}{1}\).                                 D. \(\Delta :\,\frac{x}{4}=\frac{y-1}{-2}=\frac{z+1}{1}\).

A. \(T=\frac{13}{4}\).    

B. \(T=3\).                    

C. \(T=\frac{1}{4}\).   

D. \(T=2\).

Cho hàm đa thức bậc ba \(y=f\left( x \right)\) liên tục, có đạo hàm trên \(\left[ -2;2 \right]\) và có đồ thị như hình vẽ

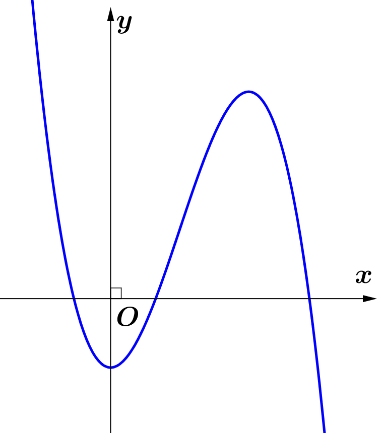
Số điểm cực tiểu của hàm số \(y=\sqrt[3]{{{\left( f\left( x \right) \right)}^{2}}}\) là

A. 1.                               

B. 2.                             

C. 3.                             

D. 5.

Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có \(f\left( -2 \right)=2;f\left( 0 \right)=1.\) Tính \(I=\int\limits_{-2}^{0}{\frac{{f}'\left( x \right)-f\left( x \right)}{{{e}^{x}}}dx}.\)

A. \(I=1-2{{e}^{2}}\).     

B. \(I=1-2{{e}^{-2}}\). 

C. \(I=1+2{{e}^{2}}\). 

D. \(I=1+2{{e}^{-2}}\).

Tập hợp các điểm biểu diễn số phức \(z\) thỏa mãn \(\left| 5z \right|=\left| \left( 4+3i \right)z-25 \right|\) là đường thẳng có phương trình

A. \(8x-6y-25=0\).          

B. \(8x-6y+25=0\).       

C. \(8x+6y+25=0\).      

D. \(8x-6y=0\).

A. \(2\).                           

B. \(4\).                         

C. \(1\).                        

D. \(3\).

Cho hình lăng trụ \({ABC.A'B'C'}\) có \(A{A}'=A{B}'=A{C}'\). Tam giác \({ABC}\) vuông cân tại \({A}\) có \({BC=2a}\). Khoảng cách từ \({A}'\) đến mặt phẳng \(\left( BC{C}'{B}' \right)\) là \(\frac{a\sqrt{3}}{3}\). Tính thể tích khối lăng trụ đã cho.

A. \({V=\frac{a^3\sqrt2}{2}}\).                           B. \({V=\frac{a^3\sqrt2}{6}}\).           C. \(V=\frac{{{a}^{3}}\sqrt{3}}{6}\).                       D. \(V=\frac{{{a}^{3}}\sqrt{3}}{3}\).

Có bao nhiêu giá trị nguyên của tham số \(m\) sao cho phương trình \(2f\left( \sin x-\cos x \right)=m-1\) có hai nghiệm phân biệt trên khoảng \(\left( -\frac{\pi }{4}\,;\,\frac{3\pi }{4} \right)\)?

A. \(13\).                          B. \(12\).                        C. \(11\).                       D. \(21\).

A. \(7\).                           

B. \(2\sqrt{53}\).          

C. \(2\sqrt{58}\).          

D. \(4\sqrt{13}\).

A. \(m\in \left( -1\,;\,0 \right)\).                           

B. \(m\in \left( -2\,;\,0 \right)\).           

C. \(m\in \left( -1\,;\,+\infty  \right)\).                                 

D. \(m\in \left[ -1\,;\,0 \right)\).

y = x⁴ - x² -2²⁰²⁰ với trục hoành 

y=1/3(m+1)x^3 + (2m-1)x^2 -(3m+2)x +m. tìm m để hàm số nghịch biến trên đoạn có độ dài bằng 4

tìm tất cả các hàm f(x²+y+f(y))=(f(x))²+2y , mọi x,y thuộc R

giúp em giải bài toán này với ạ:
tìm các giá trị của m để hàm số: y=x^3-(m+2)x+m cực tiểu tại x=1

ảnh đây ạ absfiinwanfandajngaibgierabai

1) \(y={x}^{6}{(1-x)}^{5}\)   (định lý 1,2)

2) \(y=2cos2x+1\)   (định lý 2)