-
Câu hỏi:
Trong không gian với hệ trục Oxyz.cho \(H\left( {1;4;3} \right).\) Mặt phẳng (P) qua H cắt các tia Ox, Oy, Oz tại 3 điểm là đỉnh của một tam giác nhận H làm trực tâm. Phương trình mặt phẳng (P) là:
- A. \(x + 4y + 3z + 26 = 0\)
- B. \(x + 4y + 3z - 16 = 0\)
- C. \(x - 4y - 3z + 24 = 0\)
- D. \(x - 4y - 3z + 12 = 0\)
Đáp án đúng: B
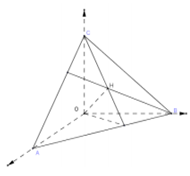
Có \(\left\{ {\begin{array}{*{20}{c}}{AB \bot CH}\\{AB \bot CO}\end{array}} \right. \Rightarrow AB \bot \left( {CHO} \right) \Rightarrow AB \bot OH\)
Tương tự: \(OH \bot AC \Rightarrow OH \bot \left( {ABC} \right)\)
Suy ra (P) nhận \(\overrightarrow {OH} = \left( {1;4;3} \right)\) làm vecto pháp tuyến
\( \Rightarrow \left( P \right):\left( {x - 1} \right) + 4\left( {y - 4} \right) + 3\left( {z - 3} \right) = 0\)
Hay \(\left( P \right):x + 4y + 3z - 26 = 0.\)
YOMEDIA
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC VỀ PHƯƠNG TRÌNH MẶT PHẲNG
- Viết phương trình mặt phẳng qua A(1;1;1) vuông góc với hai mặt phẳng x + y - z - 2 = 0 và x - y + z - 1 = 0
- Viết phương trình mặt phẳng đi qua A(1;2;3) và có VTPT n=(3;-2;-1)
- Tìm Vectơ pháp tuyến của mặt phẳng (P): x - 2y + z - 1 = 0
- Gọi (P): x/a+y/b+z/c=1 với (a>0, b>0,c>0) là mặt phẳng đi qua điểm H(1;1;2) cắt Ox, Oy, Oz lần lượt tại A, B, C sao cho tứ diện OABC có thể tích nhỏ nhất
- Viết phương trình mặt phẳng đi qua A và song song với mặt phẳng (MNP) biết M, N, P là hình chiếu vuông góc của A lên Ox, Oy, Oz
- Viết phương trình mặt phẳng qua AB và song song với CD biết A(5;1;3); B(1;6;2); C(5;0;4); D(4;0;6)
- Mặt phẳng đi qua A(2;3;1) và giao tuyến của hai mặt phẳng (x + y = 0) và (x - y + z + 4 = 0) có phương trình là:
- Vecto nào sau đây là vecto pháp tuyến của mặt phẳng (P):x-y+3=0
- Viết phương trình mặt phẳng (P) đi qua điểm M(1;2;3) và cắt cấc trục Ox, Oy, Oz lần lượt tại ba điểm A, B, C khác với gốc tọa độ O sao cho biểu thức T=1/OA^2+1/OB^2+1/OC^2 có giá trị nhỏ nhất
- Tìm phương trình của mặt phẳng (P) đi qua A và vuông góc với d biết A(1;2;0) và đường thẳng d:x+1/2=y/1=z−1/−1.






